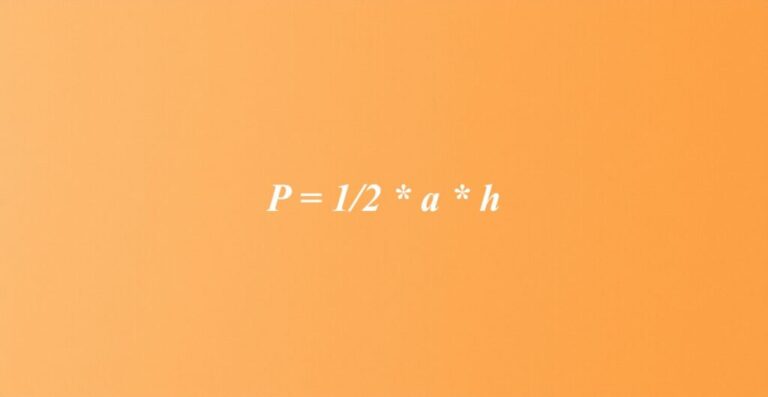Funkcje trygonometryczne

Funkcje trygonometryczne odgrywają kluczową rolę w matematyce, zwłaszcza w geometrii i analizie. Określa się je jako proporcje długości boków trójkąta prostokątnego względem jego kątów wewnętrznych. Do najważniejszych funkcji należą:

sinus,
kosinus,
tangens,
kotangens,
sekans i kosekans.

Sinus to stosunek długości przeciwprostokątnej do boku naprzeciw kąta, natomiast kosinus wyraża relację między przyprostokątną przyległą a przeciwprostokątną. Tangens to iloraz sinusa i kosinusa konkretnego kąta, a kotangens stanowi odwrotność tej relacji.

Wartości te znajdują zastosowanie w wielu dziedzinach nauki i technologii. Są niezastąpione przy modelowaniu zjawisk okresowych oraz rozwiązywaniu problemów geometrycznych czy analitycznych. Na przykład sinus i kosinus są nieodzowne przy obliczeniach związanych z ruchem falowym lub analizie sygnałów.

Na okręgu jednostkowym funkcje te można przedstawić jako współrzędne punktu dla danego kąta: współrzędna x odpowiada kosinusowi, a y – sinusowi tego kąta.

Zrozumienie symetrii, okresowości oraz miejsc zerowych tych funkcji umożliwia ich efektywniejsze wykorzystanie w praktycznych zastosowaniach oraz zaawansowanych badaniach matematycznych.

Definicje i podstawowe własności

Funkcje trygonometryczne stanowią istotny element matematyki, z szerokimi zastosowaniami w naukach ścisłych i technice. Do najważniejszych należą:

sinus (sin),
kosinus (cos),
tangens (tg),
kotangens (ctg).

Sinus i kosinus to stosunki długości boków w trójkącie prostokątnym. Sinus jest stosunkiem przeciwprostokątnej do przyprostokątnej naprzeciw kąta, natomiast kosinus to relacja przyprostokątnej przylegającej do kąta do przeciwprostokątnej.

Obydwie funkcje mają charakter okresowy z okresem \(2\pi\), a ich wartości zawierają się między -1 a 1. Sinus jest funkcją nieparzystą, co oznacza, że \(\mathrm{sin}(-x) = -\mathrm{sin}(x)\), podczas gdy kosinus jest parzysty: \(\mathrm{cos}(-x) = \mathrm{cos}(x)\).

Tangens definiuje się jako iloraz sinusa przez kosinus (\(\mathrm{tg}(x) = \frac{\mathrm{sin}(x)}{\mathrm{cos}(x)}\)), zerując się tam, gdzie sinus osiąga wartość zero. Kotangens jest odwrotnością tangensa (\(\mathrm{ctg}(x) = \frac{\mathrm{cos}(x)}{\mathrm{sin}(x)}\)). Dzięki tym cechom funkcje te są niezwykle użyteczne w analizie sygnałów czy modelowaniu procesów cyklicznych.

Warto podkreślić unikalne właściwości każdej z tych funkcji wpływające na ich zastosowanie: przykładowo, sinus wzrasta od 0 do 1 w przedziale [0, \(\frac{\pi}{2}\)], a następnie maleje; z kolei kosinus startuje od wartości 1 i zmniejsza się do -1 na tym samym przedziale. Zrozumienie tych definicji i właściwości umożliwia pełne wykorzystanie potencjału funkcji trygonometrycznych w praktyce.

Funkcje w trójkącie prostokątnym

Funkcje trygonometryczne w trójkącie prostokątnym bazują na zależnościach między długościami jego boków. Sinus kąta α to stosunek długości boku naprzeciw tego kąta do przeciwprostokątnej. Kosinus natomiast odnosi długość boku przyległego do kąta α do przeciwprostokątnej. Aby obliczyć tangens kąta α, dzielimy długość boku naprzeciw tego kąta przez długość boku przyległego.

Z kolei cotangens jest odwrotnością tangensa i reprezentuje stosunek boku przyległego do kąta α względem boku naprzeciw niego. Te funkcje są nieocenione w geometrii i trygonometrii, umożliwiając wyrażanie relacji między kątami a bokami w trójkątach prostokątnych. Dzięki nim można bez trudu wyznaczyć brakujące elementy tych figur, co jest niezwykle przydatne zarówno w zadaniach matematycznych, jak i w praktycznych zastosowaniach inżynieryjnych oraz fizycznych.

Funkcje na okręgu jednostkowym

Funkcje trygonometryczne na okręgu jednostkowym mają fundamentalne znaczenie w matematyce, umożliwiając zrozumienie związku między kątami a wartościami trygonometrycznymi. Okrąg taki charakteryzuje się promieniem równym 1 i znajduje się w układzie współrzędnych, gdzie jego środek to punkt (0,0).

Dla ostrego kąta θ, sinus θ odpowiada długości odcinka AC, co jest równoznaczne ze współrzędną y punktu C na obwodzie okręgu. Z kolei kosinus θ oznacza długość odcinka OC, czyli odpowiada współrzędnej x tego samego punktu. Tangens θ to stosunek sinusa do kosinusa i można go interpretować jako długość odcinka AE, gdzie linia przechodząca przez punkt C przecina oś y. Kotangens θ stanowi odwrotność tangensa i reprezentuje długość odcinka AF.

te pojęcia można również rozszerzyć na funkcje hiperboliczne,
które posiadają analogiczną interpretację geometryczną na płaszczyźnie zespolonej,
poznanie tych zależności upraszcza rozwiązywanie równań trygonometrycznych oraz modelowanie zjawisk okresowych za pomocą funkcji zarówno trygonometrycznych, jak i hiperbolicznych.

Podstawowe funkcje trygonometryczne

Podstawowe funkcje trygonometryczne, takie jak sinus, kosinus, tangens i kotangens, odgrywają istotną rolę w analizie trójkątów prostokątnych i modelowaniu zjawisk cyklicznych.

sinus oraz kosinus to okresowe funkcje o okresie równym 2π, których wartości mieszczą się między -1 a 1,
sinus jest nieparzysty, co oznacza, że spełnia równanie sin(-x) = -sin(x),
kosinus jest parzysty i zachowuje równanie cos(-x) = cos(x).

Tangens i kotangens charakteryzują się krótszym okresem podstawowym wynoszącym π.

tangens można zdefiniować jako stosunek sinusa do kosinusa: tg(x) = sin(x)/cos(x),
kotangens stanowi odwrotność tej relacji: ctg(x) = cos(x)/sin(x).

Te funkcje są kluczowe przy rozwiązywaniu równań trygonometrycznych oraz w analizach matematycznych.

Funkcje trygonometryczne mają szerokie zastosowanie w wielu dziedzinach nauki i techniki, takich jak:

fizyka,
inżynieria,
geografia.

Dzięki swoim wyjątkowym właściwościom umożliwiają modelowanie fal dźwiękowych lub przewidywanie ruchu planetarnego. Odgrywają także ważną rolę w zaawansowanych obliczeniach matematycznych oraz badaniach związanych ze zjawiskami cyklicznymi.

Sinus i jego właściwości

Funkcja sinus, oznaczana jako sin(x), to jedna z podstawowych funkcji trygonometrycznych w matematyce. Można ją stosować dla dowolnego kąta wyrażonego w radianach, gdyż obejmuje wszystkie liczby rzeczywiste. Wynik działania tej funkcji zawsze mieści się w przedziale od -1 do 1.

Sinus jest funkcją okresową z okresem T=2π, co oznacza, że jej wartości powtarzają się co 2π jednostek. To szczególnie przydatne przy analizie zjawisk cyklicznych i modelowaniu fal.

Dodatkowo, sinus charakteryzuje się tym, że jest funkcją nieparzystą, spełniając równanie sin(−x) = −sin(x). Ta właściwość wpływa na symetrię wykresu względem początku układu współrzędnych.

Cechuje ją również ograniczoność i zmienność w określonych zakresach:

zwiększa swoje wartości w przedziałach (−π/2 + 2kπ, π/2 + 2kπ),
zmniejsza w przedziałach (π/2 + 2kπ, 3π/2 + 2kπ),
gdzie k to liczba całkowita.

Dzięki tym właściwościom analiza jej zachowania staje się bardziej przewidywalna. Zrozumienie tych cech umożliwia efektywne wykorzystanie funkcji sinus w różnych dziedzinach nauki i techniki.

Kosinus i jego właściwości

Kosinus, oznaczany jako cos(x), to jedna z kluczowych funkcji trygonometrycznych. Jego dziedzina obejmuje wszystkie liczby rzeczywiste, a wartości zawierają się między -1 a 1. Jest to funkcja okresowa z okresem T=2π, co oznacza, że po 2π jednostkach kąta zaczyna się powtarzać. Dodatkowo jest parzysta, charakteryzuje ją symetria względem osi y: cos(−x) = cos(x).

Zakres wartości kosinusa jest ograniczony:

maksimum wynosi 1,
minimum -1.

Funkcja ta wykazuje właściwości monotoniczne — zwiększa swoją wartość w przedziałach (π + 2kπ, 2π + 2kπ) i zmniejsza w przedziałach (0 + 2kπ, π + 2kπ), gdzie k to liczba całkowita. Punkty zerowe kosinusa można znaleźć w miejscach o postaci (2k+1)π/2.

Dzięki swojej regularnej strukturze i symetrii kosinus jest szeroko używany w matematyce oraz naukach stosowanych do modelowania zjawisk okresowych.

Tangens i cotangens

Tangens i cotangens to istotne funkcje trygonometryczne, każda z nich charakteryzuje się wyjątkowymi właściwościami.

tangens, oznaczany jako tg(x), jest wyrażony jako stosunek sinusa do kosinusa: tg(x) = sin(x)/cos(x),
jego dziedzinę stanowią wszystkie liczby rzeczywiste poza punktami x = π/2 + kπ, gdzie k to dowolna liczba całkowita (k∈Z),
w takich miejscach kosinus przyjmuje wartość zero, co prowadzi do nieokreśloności,
istnieje możliwość przypisania wartości tangensa do każdej liczby rzeczywistej,
jest funkcją okresową z okresem T=π, a także rosnącą i nieparzystą, spełniającą relację tg(-x) = -tg(x).

Cotangens (ctg(x)), w przeciwieństwie do tangensa, jest definiowany jako cos(x)/sin(x).

jego dziedzina wyklucza punkty x=kπ, gdyż w tych punktach sinus równa się zero,
podobnie jak tangens, cotangens ma okres T=π i jest również funkcją nieparzystą,
zbiór jego wartości obejmuje całość liczb rzeczywistych.

Poznanie tych właściwości ułatwia wykorzystanie obu funkcji w analizie matematycznej oraz w rozwiązywaniu równań trygonometrycznych.

Własności okresowe i symetria

Funkcje trygonometryczne wyróżniają się okresowością i symetrią, co wpływa na ich zachowanie oraz sposób, w jaki prezentują się na wykresach. Sinus i kosinus charakteryzują się okresem 2π, podczas gdy tangens i cotangens mają okres równy π. Oznacza to regularność w powtarzaniu się ich wartości.

sinus jest funkcją nieparzystą, więc spełnia zależność sin(-x) = -sin(x),
kosinus jest parzysty, co przejawia się równaniem cos(-x) = cos(x),
podobnie jak sinus, tangens również jest nieparzysty: tan(-x) = -tan(x).

Symetria względem osi układów współrzędnych odgrywa kluczową rolę przy analizie wykresów tych funkcji oraz przy rozwiązywaniu równań trygonometrycznych. Dziedzina sinusa i kosinusa obejmuje wszystkie liczby rzeczywiste z wartościami między -1 a 1. Natomiast dziedzina tangensa wyklucza kąty o mierze (π/2 + kπ), gdzie k jest dowolną liczbą całkowitą.

Poznanie tych właściwości umożliwia lepsze modelowanie zjawisk fizycznych oraz skuteczne rozwiązywanie problemów matematycznych związanych z cyklicznością procesów.

Wykresy i miejsca zerowe funkcji trygonometrycznych

Funkcje trygonometryczne, takie jak sinus i kosinus, charakteryzują się unikalnymi wykresami, które są kluczowe dla ich zrozumienia.

wykres sinusa przybiera formę sinusoidy,
jego okres wynosi 2π i oscyluje od -1 do 1,
rozpoczyna się w punkcie zerowym (x = 0),
osiąga szczyt przy x = π/2,
wraca do zera na x = π,
spada do minimum przy x = 3π/2,
kończy cykl ponownie na zerze przy x = 2π.

w przypadku kosinusa mamy cosinusoidę o takim samym okresie 2π,
startuje ona od maksymalnej wartości (y = 1) gdy x = 0,
przechodzi przez zero w momencie x = π/2,
osiąga dno (y = -1) przy x = π,
ponownie przecina oś poziomą na x = 3π/2,
zamyka cały cykl maksymalną wartością w punkcie x = 2π.

Istotne są również miejsca zerowe tych funkcji:

dla sinusa pojawiają się one w punktach typu x = kπ (gdzie k jest liczbą całkowitą),
kosinus natomiast ma zera w punktach określonych jako x = (2k+1)π/2,
tangens dzieli swoje miejsca zerowe z sinusem w punktach kπ,
cotangens ma je podobnie jak kosinus dla punktów kπ.

Zrozumienie wykresów oraz miejsc zerowych tych funkcji stanowi fundament analizy ich właściwości oraz rozwiązywania równań trygonometrycznych.

Wykresy sinus i kosinus

Wykresy sinusoidy i kosinusoidy stanowią kluczowe przykłady funkcji okresowych w matematyce. Sinusoida, zapisywana jako y = sin(x), charakteryzuje się falistym kształtem z okresem równym 2π, a jej wartości wahają się od -1 do 1. Kosinusoidę, oznaczaną jako y = cos(x), cechuje podobny wzór, lecz jest przesunięta o π/2 na lewo względem sinusoidy.

Zmiany trygonometryczne modyfikują wygląd tych wykresów. Przykładowo, zwiększając amplitudę w funkcji y = 2sin(x), powodujemy rozszerzenie lub skurczenie wykresu w osi pionowej. Natomiast zmiana okresu przez modyfikację współczynnika przed x, jak w przypadku y = sin(2x), skraca okres do π i sprawia, że fale stają się gęstsze na tej samej długości osi poziomej.

Takie przekształcenia umożliwiają dostosowanie funkcji sinus i kosinus do różnorodnych zastosowań praktycznych oraz modelowania zjawisk cyklicznych. Przykładami takich zastosowań są:

analiza sygnałów,
modelowanie ruchów harmonicznych w dziedzinie fizyki.

Miejsca zerowe sinus, kosinus, tangens i cotangens

Miejsca zerowe funkcji trygonometrycznych odgrywają znaczącą rolę w matematyce.

dla sinusa, pojawiają się one w punktach x = kπ, gdzie k jest liczbą całkowitą,
innymi słowy, sinus osiąga wartość zero dla każdej wielokrotności liczby π,
jeśli chodzi o kosinus, jego miejsca zerowe występują przy x = (2k+1)π/2,
oznacza to, że kosinus znika przy nieparzystych wielokrotnościach π/2,
tangens dzieli te same miejsca zerowe co sinus, a więc także w punktach x = kπ,
cotangens natomiast również przyjmuje wartość zero tam samo jak tangens – czyli ponownie, x = kπ.

Poznanie tych miejsc zerowych jest kluczowe podczas rozwiązywania równań trygonometrycznych i badania wykresów funkcji trygonometrycznych. Wiedza ta jest cenna zarówno w teorii, jak i praktyce matematyki oraz fizyki, ponieważ te funkcje często modelują zjawiska okresowe.

Funkcje odwrotne i hiperboliczne

Funkcje odwrotne, takie jak arcsin, arccos i arctan, odgrywają kluczową rolę w matematyce przy rozwiązywaniu równań trygonometrycznych. Arcsin x jest określony dla wartości x między -1 a 1, przyjmując wyniki z zakresu od -π/2 do π/2. Z kolei arccos x działa w przedziale od 0 do π. Natomiast arctan x obejmuje całą oś liczbową, dając wyniki pomiędzy -π/2 a π/2.

Funkcje hiperboliczne są podobne do trygonometrycznych, jednak bazują na funkcjach wykładniczych. Do najpopularniejszych należą:

sinh (sinus hiperboliczny),
cosh (kosinus hiperboliczny),
tanh (tangens hiperboliczny).

Charakteryzują się unikalnymi właściwościami matematycznymi, co czyni je niezwykle przydatnymi w dziedzinach takich jak fizyka czy inżynieria.

Jednoznaczność definicji funkcji odwrotnych w ograniczonych przedziałach ma istotne znaczenie. Pozwala to precyzyjnie określić kąty odpowiadające konkretnym stosunkom boków w trójkątach prostokątnych lub punktom na okręgu jednostkowym. Te funkcje znajdują szerokie zastosowanie zarówno w teorii, jak i w praktycznych obliczeniach.

Funkcje odwrotne: arcsin, arccos, arctan

Funkcje odwrotne do trygonometrycznych, takie jak arcsin, arccos czy arctan, odgrywają istotną rolę w matematyce.

arcsin x działa w przedziale od -1 do 1 i zwraca kąty w zakresie od -π/2 do π/2 radianów,
arccos x również przyjmuje wartości w tym samym zakresie, ale generuje kąty od 0 do π radianów,
arctan x jest zdefiniowany dla wszystkich liczb rzeczywistych i zwraca kąty pomiędzy -π/2 a π/2 radianów.

Te funkcje są niezwykle ważne przy rozwiązywaniu równań trygonometrycznych oraz wszędzie tam, gdzie potrzebne są przekształcenia odwrotne.

Na przykład pomagają wyznaczyć miarę kąta na podstawie znanej wartości funkcji trygonometrycznej. Dodatkowo znajdują zastosowanie w modelowaniu zjawisk fizycznych oraz analizie sygnałów, szczególnie gdy trzeba określić kąt bazując na proporcji boków lub stosunku funkcji trygonometrycznych.

Funkcje hiperboliczne i ich właściwości

Funkcje hiperboliczne, takie jak sinh (sinus hiperboliczny), cosh (cosinus hiperboliczny) oraz tanh (tangens hiperboliczny), przypominają funkcje trygonometryczne, jednak dotyczą hiperboli, a nie okręgu.

Sinh(x) można zapisać jako \(\frac{e^x – e^{-x}}{2}\), natomiast cosh(x) to \(\frac{e^x + e^{-x}}{2}\). Tanh(x) stanowi stosunek sinh(x) do cosh(x).

Podobnie jak ich trygonometryczne odpowiedniki, te funkcje wykazują symetrię:

sinh jest funkcją nieparzystą (\(sinh(-x) = -sinh(x)\)), co oznacza symetrię względem początku układu współrzędnych,
cosh jest parzysta (\(cosh(-x) = cosh(x)\)), co wskazuje na symetrię względem osi y.

Chociaż funkcje trygonometryczne są okresowe z uwagi na jednostkowy okrąg, funkcje hiperboliczne zachowują się odmiennie. Ich wartości rosną wykładniczo w miarę oddalania się od zera, co je odróżnia od sinusów i kosinusów związanych z ruchem harmonicznym.

Funkcje te mają istotne znaczenie w matematyce i fizyce, zwłaszcza przy rozwiązywaniu równań różniczkowych dotyczących fal czy przewodnictwa cieplnego. Ponadto, dzięki swoim wyjątkowym właściwościom, znajdują zastosowanie w teorii względności oraz obliczeniach inżynierskich.

Zaawansowane aspekty funkcji trygonometrycznych

Zaawansowane aspekty funkcji trygonometrycznych obejmują zarówno wzory redukcyjne, jak i tożsamości trygonometryczne. Wzory te odgrywają kluczową rolę w obliczaniu wartości funkcji dla kątów poza zakresem ostrych.

w sumie istnieje 28 takich wzorów,
umożliwiają przekształcanie wyrażeń,
dowodzą różnych równań.

Dzięki nim można znacząco uprościć złożone wyrażenia trygonometryczne, co okazuje się niezwykle przydatne w skomplikowanych obliczeniach matematycznych.

Tożsamości trygonometryczne to równania zawsze prawdziwe niezależnie od wartości kąta, jak na przykład \( \sin^2(x) + \cos^2(x) = 1 \). Stanowią one fundament wielu zaawansowanych rozważań matematycznych i fizycznych.

W praktyce inżynierskiej oraz naukach stosowanych przekształcenia te mają istotne znaczenie nie tylko w teorii, ale także podczas modelowania zjawisk okresowych czy analizy sygnałów w dziedzinach czasu i częstotliwości.

Wzory redukcyjne i tożsamości trygonometryczne

Wzory redukcyjne w trygonometrii to kluczowe narzędzia, które ułatwiają przekształcanie wyrażeń trygonometrycznych. Pozwalają one na dokonywanie obliczeń dla dowolnych kątów, opierając się na kątach ostrych. Przykładowo:

sin(90°-α) równa się cosα,
cos(90°-α) to sinα,
tg(90°-α) odpowiada ctgα.

Dzięki tym wzorom możliwe jest uproszczenie złożonych wyrażeń i obliczenie wartości funkcji trygonometrycznych także dla kątów spoza standardowego zakresu.

Tożsamości trygonometryczne stanowią podstawowe równania łączące różnorodne funkcje trygonometryczne. Są one przydatne do wykazywania równości między różnymi wyrażeniami oraz upraszczania skomplikowanych równań. Na przykład, tożsamość pitagorejska: sin²θ + cos²θ = 1 ilustruje relację między sinusami a kosinusami tego samego kąta.

Znajomość wzorów redukcyjnych i tożsamości jest kluczowa przy rozwiązywaniu problemów matematycznych związanych z funkcjami trygonometrycznymi. Jest ona niezbędna zarówno w analizie matematycznej, jak i w zastosowaniach fizycznych modelujących zjawiska okresowe.

Rozwinięcia w szeregi potęgowe

Rozwijanie funkcji trygonometrycznych, takich jak sinus i kosinus, w szeregi potęgowe odgrywa kluczową rolę w analizie matematycznej. Dzięki temu możemy przedstawić te funkcje jako nieskończone sumy:

sinus x można wyrazić jako \(\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!} x^{2n+1}\),
kosinus x jako \(\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n)!} x^{2n}\).

Takie rozwinięcia są niezwykle przydatne przy rozwiązywaniu złożonych równań różniczkowych oraz wspomagają analizy numeryczne i komputerowe przybliżenia wartości. To szczególnie istotne w dziedzinach inżynierii i fizyki. Szeregi potęgowe nie są jedynie teorią, lecz także praktycznym narzędziem do rozwiązywania problemów związanych z modelowaniem zjawisk okresowych oraz obliczeniami numerycznymi.

Wzór Eulera i związki z funkcją wykładniczą

Formuła Eulera, wyrażona jako e^(ix) = cos(x) + i*sin(x), łączy trygonometrię z funkcją wykładniczą. Dzięki niej możemy dostrzec, jak liczby zespolone wpływają na wyrażenia trygonometryczne oraz wykładnicze. Ukazuje ona, że wyrażenie wykładnicze dla liczby zespolonej jest związane z jej kosinusem oraz sinusoidalną składową.

Funkcja wykładnicza przybiera formę e^(ix), gdzie 'i’ oznacza jednostkę urojoną, a 'x’ to kąt w radianach. Wzór ten pozwala przekształcać równania trygonometryczne w postacie użyteczne w analizie zespolonej. Jest powszechnie stosowany w dziedzinach takich jak inżynieria elektryczna czy fizyka kwantowa, pomagając modelować zjawiska falowe i oscylacyjne.

Równania i nierówności trygonometryczne

Równania i nierówności trygonometryczne pełnią istotną funkcję w matematyce, zwłaszcza w dziedzinie analizy. Zawierają one takie funkcje jak sinus, cosinus i tangens, koncentrując się na odnajdywaniu kątów spełniających dane warunki.

Przykładowo, równanie \( \sin(x) = 0.5 \) wymaga ustalenia, dla jakich wartości \( x \) sinus osiąga wartość 0.5. W tym procesie kluczowe jest wykorzystanie tożsamości trygonometrycznych oraz analizowanie wykresów.

Nierówności trygonometryczne z kolei wymagają rozpatrzenia przedziałów, aby określić zakresy, w których funkcje są większe lub mniejsze od podanej liczby. Na przykład przy nierówności \( \cos(x) > 0 \), należy znaleźć te kąty, dla których cosinus jest dodatni. Przy rozwiązaniu takich zadań często korzysta się z wykresów i okresowości tych funkcji.

W praktyce zastosowanie równań i nierówności trygonometrycznych jest szerokie:

modelowanie zjawisk cyklicznych,
rozwiązywanie problemów inżynieryjnych i fizycznych,
opis ruchu falowego,
obliczenia związane z oscylacjami harmonicznymi.

Pozwalają one na opis ruchu falowego czy obliczenia związane z oscylacjami harmonicznymi, co czyni je niezastąpionym narzędziem w wielu obszarach nauki i technologii.

Rozwiązywanie równań trygonometrycznych

Rozwiązywanie równań trygonometrycznych opiera się na zrozumieniu podstawowych pojęć, takich jak sinus, kosinus i tangens oraz ich tożsamości. Kluczowym etapem jest sprowadzenie równania do formy umożliwiającej wyznaczenie wartości kątów. Często w tym procesie korzysta się z tożsamości trygonometrycznych, na przykład wzorów sumy i różnicy kątów czy podwójnego kąta.

Weźmy jako przykład równanie \(\sin(x) = 0.5\). Aby znaleźć rozwiązania, musimy ustalić kąty \(x\), dla których sinus wynosi 0.5. W tym przypadku są to \(30^\circ\) i \(150^\circ\), co odpowiada \(\frac{\pi}{6}\) oraz \(\frac{5\pi}{6}\) w radianach.

Często pomocne są również przekształcenia algebraiczne, takie jak wyciąganie wspólnego czynnika przed nawias lub zamiana funkcji na ich odwrotności (np. arcsin). Dla bardziej skomplikowanych równań można używać metod numerycznych lub graficznych w celu znalezienia przybliżonych rozwiązań.

W praktyce rozwiązywanie tego typu równań często obejmuje analizę okresowości funkcji oraz symetrii wykresu. Pozwala to zidentyfikować wszystkie możliwe rozwiązania w danym przedziale i efektywnie odpowiadać na zaawansowane pytania związane z funkcjami trygonometrycznymi.

Nierówności trygonometryczne

Nierówności trygonometryczne polegają na określaniu, w jakich przedziałach wartości funkcje takie jak sinus, kosinus, tangens czy cotangens są większe lub mniejsze od pewnej liczby. Kluczowym elementem w rozwiązywaniu takich nierówności jest zrozumienie wykresów oraz podstawowych cech tych funkcji.

dzięki okresowości sinusa i kosinusa (obie mają okres \(2\pi\)), możemy przewidzieć momenty osiągania ich ekstremalnych wartości,
sinus osiąga wartość maksymalną równą 1 przy kącie \(\frac{\pi}{2}\), a minimalną -1 przy kącie \(\frac{3\pi}{2}\),
kosinus również osiąga te same wartości przy odpowiednich przesunięciach fazowych.

Podczas analizy nierówności trygonometrycznych warto zwrócić uwagę na symetrię funkcji. Sinus jest symetryczny względem początku układu współrzędnych, co oznacza symetrię względem osi Y. Z kolei kosinus charakteryzuje się symetrią względem osi X. Te właściwości ułatwiają identyfikację zakresów spełniających daną nierówność.

Przykład: Rozważmy nierówność \(\sin(x) > \frac{1}{2}\). Z wykresu sinusa wiemy, że ta nierówność zachodzi dla przedziału \(x \in (\frac{\pi}{6} + 2k\pi,\frac{5\pi}{6} + 2k\pi)\), gdzie \(k\) to dowolna liczba całkowita. To pokazuje znaczenie znajomości wykresu i właściwości funkcji przy rozwiązywaniu tego typu problemów.

Zastosowania funkcji trygonometrycznych

Funkcje trygonometryczne odgrywają istotną rolę w różnych dziedzinach nauki i techniki, umożliwiając modelowanie zjawisk o charakterze okresowym. W geometrii są nieocenione przy wyznaczaniu długości boków oraz kątów trójkątów, co jest kluczowe w rozwiązywaniu zagadnień związanych z konstrukcjami geometrycznymi. Również w analizie matematycznej funkcje te pozwalają na tworzenie szeregów Fouriera, które przedstawiają funkcje jako sumę sinusoid, co ma zastosowanie w przetwarzaniu sygnałów i analizie dźwięku.

W fizyce funkcje te opisują ruch harmoniczny, jak np. oscylacje wahadła czy drgania sprężyn. Z kolei w akustyce służą do analizy fal dźwiękowych i projektowania systemów nagłośnienia. Astronomowie korzystają z nich do obliczeń pozycji ciał niebieskich oraz przewidywania zaćmień.

Inżynieria oraz robotyka również czerpią korzyści z trygonometrii przy projektowaniu precyzyjnych mechanizmów i sterowaniu ruchem robotów, co umożliwia konstruowanie skomplikowanych maszyn przemysłowych czy pojazdów autonomicznych.

Kolejnym polem zastosowania tych funkcji jest modelowanie zjawisk cyklicznych, dzięki czemu można dokładnie opisać procesy takie jak zmiany klimatyczne czy oscylacje ekonomiczne. To wszechstronne narzędzie matematyczne znajduje zastosowanie wszędzie tam, gdzie regularność i cykliczność są kluczowe.

Modelowanie zjawisk okresowych

Modelowanie zjawisk okresowych przy użyciu funkcji trygonometrycznych ma fundamentalne znaczenie w naukach przyrodniczych i technologii. Funkcje takie jak sinus i kosinus świetnie opisują procesy cykliczne dzięki swoim okresowym właściwościom. Przykładowo, fale dźwiękowe można przedstawiać jako funkcje sinusoidalne o specyficznej częstotliwości oraz amplitudzie. Podobnie, ruch planet w Układzie Słonecznym cechuje się cyklicznością, co czyni modele bazujące na funkcjach trygonometrycznych doskonałym rozwiązaniem.

Funkcja okresowa charakteryzuje się regularnym powtarzaniem wartości w czasie, co pozwala przewidywać przyszłe zachowania systemu na podstawie wcześniejszych obserwacji. W praktyce przekłada się to na większą precyzję prognoz oraz umożliwia optymalizację różnorodnych procesów technologicznych i naukowych.

Co więcej, zastosowanie funkcji trygonometrycznych wykracza poza matematykę teoretyczną. Odtwarzają one istotną rolę w analizie sygnałów elektrycznych oraz w analityce finansowej, gdzie rozpoznawanie cyklicznych wzorców jest kluczowe dla podejmowania decyzji.

Zastosowania w analizie matematycznej

Funkcje trygonometryczne odgrywają kluczową rolę w matematyce, zwłaszcza podczas analizy szeregów potęgowych oraz równań różniczkowych. Dzięki szeregom Fouriera, które łączą funkcje trygonometryczne, możliwe jest efektywne analizowanie sygnałów i przetwarzanie danych. Te szeregi pozwalają na dekompozycję sygnałów na składowe harmoniczne, co znacząco ułatwia ich badanie i interpretację. W kontekście równań różniczkowych funkcje te wspierają rozwiązywanie problemów związanych z oscylacjami oraz modelowaniem dynamicznych zjawisk. Z tego powodu stanowią niezastąpione narzędzia w zaawansowanej matematyce i inżynierii.

Praktyczne metody obliczeń

Praktyczne zastosowanie funkcji trygonometrycznych jest kluczowe w licznych dziedzinach, takich jak geodezja, nawigacja czy inżynieria. W przypadku geodezji, te funkcje umożliwiają precyzyjne określanie wysokości budynków oraz szerokości rzek poprzez analizę kątów i odległości.

znajomość kąta nachylenia i poziomej odległości do wierzchołka budynku pozwala łatwo obliczyć jego wysokość,
w nawigacji trygonometria służy do ustalania pozycji statku lub samolotu względem wyznaczonego punktu odniesienia,
dzięki niej można dokładnie określić zarówno kurs, jak i prędkość jednostki poruszającej się po wodzie lub w powietrzu.

Inżynierowie wykorzystują te funkcje przy analizie strukturalnej mostów czy dróg, zwracając uwagę na siły działające pod różnymi kątami. Przy projektowaniu mostu konieczne jest uwzględnienie wpływu ciężaru oraz innych czynników zewnętrznych na konstrukcję.

Funkcje trygonometryczne są również nieocenione w modelowaniu zjawisk okresowych oraz analizie dynamicznych systemów mechanicznych. Stanowią fundament wielu współczesnych metod obliczeniowych stosowanych w nauce i technice.