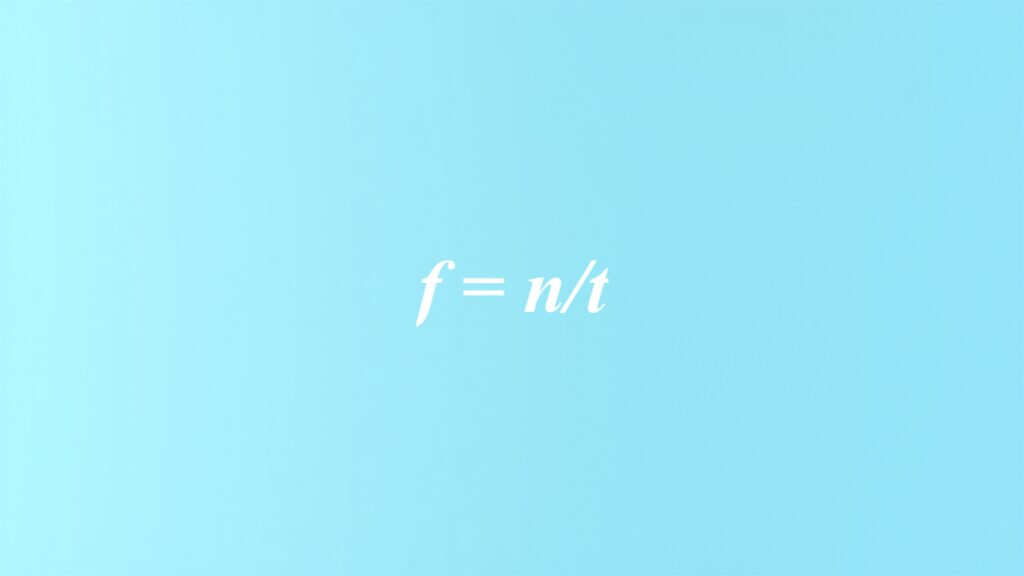Jaki jest wzór na częstotliwość?
Częstotliwość to istotne pojęcie w fizyce, które określa, ile razy zjawisko okresowe powtarza się w określonym czasie. Symbolizujemy ją literą f i mamy różne metody jej obliczania.
- pierwszy sposób to wzór f = n/t, gdzie n oznacza liczbę drgań, a t czas w sekundach,
- alternatywnie możemy użyć wzoru f = 1/T, przydatnego, gdy znamy długość jednego pełnego cyklu.
W przypadku ruchu obrotowego stosujemy wzór f = ω/(2π), gdzie ω jest pulsacją lub częstością kołową — miernikiem prędkości kątowej. Dzięki temu przeliczamy prędkość kątową na częstotliwość liniową. Te formuły odgrywają kluczową rolę podczas analizy fal i oscylacji.
Jednostką częstotliwości jest herc [Hz], co odpowiada jednemu cyklowi na sekundę. Wspomniane wzory umożliwiają precyzyjne określenie parametrów związanych zarówno z ruchem sinusoidalnym, jak i innymi rodzajami drgań oraz falami.
Wzór f = n/t
Wzór f = n/t stanowi podstawowe narzędzie do obliczania częstotliwości w zjawiskach cyklicznych. Oznacza to, że częstotliwość (( f )) określa liczbę drgań (( n )) wykonanych w określonym czasie (( t )). Przykładowo, gdy w ciągu 10 sekund występuje 50 drgań, częstotliwość wynosi 5 Hz. Jest to istotny parametr przy opisie dynamiki zjawisk takich jak oscylacje czy fale dźwiękowe.
Wzór f = 1/T
Wzór odgrywa kluczową rolę w analizie drgań periodycznych, ukazując związek między częstotliwością a okresem. Częstotliwość (f) definiuje się jako liczbę cykli następujących w jednostce czasu, natomiast okres (T) to czas trwania jednego pełnego cyklu. Dzięki tej formule łatwo zauważymy, że im dłuższy okres, tym niższa częstotliwość — i odwrotnie. Znajomość jednego z tych parametrów pozwala na szybkie obliczenie drugiego. Ta zależność ma szerokie zastosowanie w różnych dziedzinach nauki i techniki.
Wzór f = omega/(2*pi)
Wzór f = ω/(2π) pozwala na obliczenie częstotliwości w ruchach obrotowych. W nim, ω oznacza pulsację, czyli częstość kątową mierzona w radianach na sekundę. To istotny związek przy badaniu ruchów obrotowych i drgań, umożliwiający precyzyjne określenie liczby pełnych cykli obracającego się przedmiotu w ciągu sekundy.
Częstotliwość (f) wyrażana jest w hercach (Hz), co wskazuje liczbę cykli na sekundę. Dzięki temu wzorowi można zamienić prędkość kątową na częstotliwość liniową, co jest kluczowe w wielu dziedzinach fizyki i inżynierii, takich jak mechanika czy elektrotechnika.
Przykładowo, jeśli prędkość kątowa wirującego dysku wynosi 6 rad/s, jego częstotliwość to około 0,955 Hz.
Okres i częstotliwość drgań
Okres drgań ( T ) oraz częstotliwość ( f ) to kluczowe pojęcia w analizie ruchu oscylacyjnego. Okres jest czasem, jaki potrzebny jest na wykonanie jednego pełnego cyklu drgań, natomiast częstotliwość określa ilość tych cykli w jednostce czasu, zazwyczaj mierzonej w sekundach. Między tymi wartościami istnieje prosty związek: częstotliwość stanowi odwrotność okresu, co opisuje wzór ( f = 1/T ).
Oznacza to, że znając jeden z tych parametrów, można łatwo obliczyć drugi. Przykładowo, jeśli okres wynosi 2 sekundy, wtedy częstotliwość wynosi ( f = 1/2 ) Hz lub inaczej mówiąc 0,5 Hz. Im krótszy okres, tym większa częstotliwość. Zrozumienie tej relacji jest istotne przy badaniu różnych systemów mechanicznych i falowych.
Związek między okresem a częstotliwością
Okres i częstotliwość łączą się równaniem T = 1/f, gdzie T symbolizuje okres, a f – częstotliwość. Oznacza to, że okres jest odwrotnie proporcjonalny do częstotliwości. Przykładowo, jeśli częstotliwość wynosi 2 Hz, wtedy okres wynosi 0,5 sekundy. Wzrost częstotliwości prowadzi do skrócenia okresu. To matematyczne powiązanie ilustruje relację między tymi dwoma parametrami w kontekście drgań i fal.
Jednostki i obliczenia związane z częstotliwością
W układzie SI jednostką częstotliwości jest herc [Hz], co oznacza jeden cykl na sekundę. To fundamentalna miara w takich dziedzinach jak fizyka i inżynieria. Częstotliwość można obliczać przy użyciu różnych wzorów, zależnie od sytuacji. Na przykład, dla ruchu obrotowego oraz drgań stosujemy wzór ( f = N/t ), gdzie ( N ) to liczba cykli, a ( t ) oznacza czas w sekundach.
W praktyce herc opisuje zjawiska związane z drganiami, falami oraz napięciami elektrycznymi. Przykładowo, fale dźwiękowe o częstotliwości 440 Hz stanowią standardowy dźwięk „A” wykorzystywany do strojenia instrumentów muzycznych. Dzięki temu herc odgrywa istotną rolę w precyzyjnym opisie i analizie wielu procesów fizycznych.
Jednostka częstotliwości: herc [Hz]
Jednostka częstotliwości, znana jako herc (Hz), wskazuje liczbę cykli w ciągu sekundy. Gdy urządzenie pracuje z częstotliwością 1 Hz, oznacza to, że wykonuje jeden pełny cykl w jednej sekundzie. W bardziej zaawansowanych dziedzinach, takich jak telekomunikacja czy elektronika, używa się często większych jednostek:
- kiloherców (kHz),
- megaherców (MHz),
- gigaherców (GHz).
Na przykład 1 kHz odpowiada 1000 Hz. Z kolei 1 MHz to milion Hz, a 1 GHz to miliard Hz. Dzięki tym jednostkom można precyzyjnie określić częstotliwość w różnych technologicznych zastosowaniach.