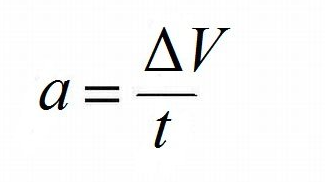Wzór na przyspieszenie

Co to jest przyspieszenie?

Przyspieszenie to wektorowa wielkość fizyczna, która określa zmiany prędkości obiektu w czasie. Dzięki niemu możemy zrozumieć, jak szybko zmieniają się zarówno wartość prędkości, jak i kierunek ruchu.

W praktyce przyspieszenie obrazuje zarówno wzrost, jak i spadek prędkości, a także wszelkie zmiany kierunków ruchu. Można je opisać jako pochodną prędkości w odniesieniu do czasu, co jest niezwykle istotne w badaniach nad ruchem, zarówno w kinematyce, jak i dynamice.

Ta wielkość pozwala nam lepiej zrozumieć ewolucję prędkości ciała, uwzględniając różne czynniki wpływające na jego ruch. Przyspieszenie więc odgrywa kluczową rolę w analizie dynamiki obiektów.

Jak przyspieszenie opisuje zmiany prędkości?

Przyspieszenie to termin oznaczający każdą zmianę prędkości obiektu, która może dotyczyć zarówno jej wartości, jak i kierunku. Ponadto, ponieważ jest to wielkość wektorowa, kierunek przyspieszenia odpowiada kierunkowi zmiany wektora prędkości Δv. Dzięki temu możemy zrozumieć, w jakim tempie oraz w którą stronę zachodzi zmiana prędkości podczas ruchu.

Możemy mieć do czynienia z:

• dodatnim przyspieszeniem, które sygnalizuje wzrost prędkości,
• przyspieszeniem ujemnym, które wskazuje na opóźnienie.

Przyspieszenie stanowi niezwykle użyteczne narzędzie do precyzyjnego opisu, jak dynamicznie zmienia się prędkość obiektu w czasie.

Zmiana wartości i kierunku prędkości

Przyspieszenie zachodzi, gdy następuje zmiana w prędkości lub jej kierunku. W kontekście ruchu prostoliniowego głównie rozpatrujemy zmiany wartości prędkości, które mogą być określane jako przyspieszenie lub opóźnienie. Natomiast w przypadku ruchu krzywoliniowego możemy wyróżnić dwa typy przyspieszenia:

• przyspieszenie styczne, które wpływa na szybkość obiektu,
• przyspieszenie normalne (dośrodkowe), które zmienia kierunek prędkości.

To drugie zjawisko jest kluczowe, ponieważ pozwala na zmianę ścieżki ruchu. Przykładem mogą być sytuacje, gdy poruszamy się po okręgu. W tym przypadku zmiana kierunku zachodzi bez modyfikacji wartości prędkości, co sprawia, że przyspieszenie jest skierowane prostopadle do wektora prędkości. Warto zaznaczyć, że przyspieszenie obejmuje zarówno zmiany w wartości prędkości, jak i w kierunku tego wektora.

Pojęcia: wektor, kierunek, zwrot

Wektor to szczególna wielkość fizyczna, która charakteryzuje się trzema kluczowymi aspektami: wartością, kierunkiem i zwrotem. Kierunek informuje nas, w którą stronę działa dana siła, natomiast zwrot precyzuje orientację wektora w obrębie tego kierunku. Na przykład, wektor przyspieszenia wskazuje kierunek, w którym następuje zmiana prędkości, choć nie zawsze jest on zgodny z kierunkiem ruchu obiektu.

Zwrot wektora przyspieszenia odzwierciedla, czy mamy do czynienia z:

• przyspieszeniem dodatnim, które współczesny z przyspieszeniem,
• opóźnieniem, które działa w przeciwną stronę.

W kontekście ruchu obrotowego wektor przyspieszenia kątowego ma charakter pseudowektora. Kierunek tego wektora wyznacza reguła prawej śruby, wskazując oś obrotu oraz określając, czy ruch jest zgodny z kierunkiem wskazówek zegara, czy też przeciwny.

To rozróżnienie między wektorem, kierunkiem a zwrotem jest niezbędne do precyzyjnego opisu dynamiki ruchu, zwłaszcza w sytuacjach, kiedy dochodzi do zmian w prędkości i kierunku poruszania się obiektów.

Jak brzmi wzór na przyspieszenie?

Podstawowy wzór związany z przyspieszeniem brzmi a = Δv/Δt. W tej formule ’a’ reprezentuje przyspieszenie, ’Δv’ oznacza zmianę prędkości, natomiast ’Δt’ to czas, w którym ta zmiana występuje. Dzięki temu równaniu jesteśmy w stanie obliczyć średnie przyspieszenie obiektu, który porusza się z określoną zmianą prędkości w danym czasie.

Dodatkowo, w ramach dynamiki, przyspieszenie można opisać poprzez drugą zasadę dynamiki Newtona. Wzór a = F/m ukazuje, jak wypadkowa siła F działająca na dany obiekt wiąże się z jego masą m. To połączenie umożliwia lepsze zrozumienie, w jaki sposób siła oddziałuje na przyspieszenie ciała.

Wykorzystanie wzoru a = Δv/Δt jest niezwykle ważne w analizie różnych typów ruchu. Stanowi to fundament zarówno kinematyki, jak i dynamiki, umożliwiając szeroką interpretację zjawisk związanych z ruchem.

Wzór a = Δv/Δt

Wzór a = Δv/Δt ukazuje przyspieszenie jako proporcję zmiany prędkości (Δv) do czasu, w jakim ta zmiana miała miejsce (Δt). Wartość Δv oznacza różnicę pomiędzy prędkością końcową a prędkością początkową.

Dzięki temu wzorowi możemy łatwo obliczyć średnie przyspieszenie w danym okresie. To narzędzie jest niezwykle istotne, gdy analizujemy:

• ruch jednostajnie przyspieszony,
• inne formy ruchu, w których prędkość ulega zmianie.

Przyspieszenie ilustruje, jak szybko prędkość obiektu zmienia się w danej jednostce czasu.

Pochodna prędkości po czasie

Pochodna prędkości względem czasu to ważne pojęcie matematyczne, które ilustruje, jak zmienia się prędkość w danej chwili. Przykładowo, wspomniane chwilowe przyspieszenie można zdefiniować jako granicę średniego przyspieszenia w momencie, gdy czas dąży do zera. W matematyce zapisujemy to jako a(t) = dv/dt, co w praktyce oznacza, że chwilowe przyspieszenie a(t) jest pochodną prędkości v(t) względem czasu t.

To pojęcie jest niezwykle pomocne w analizie ruchu zmiennego. Uwzględnia ono nie tylko zmiany prędkości, ale także kierunek ruchu. Pochodna prędkości względem czasu odgrywa kluczową rolę w kinematyce, pozwalając nam na:

• szczegółowy opis dynamiki ruchu,
• analizowanie zmian prędkości w czasie,
• rozpoznawanie kierunku ruchu.

Drugie pochodne położenia po czasie

Druga pochodna położenia w odniesieniu do czasu jest matematycznym ujęciem przyspieszenia. Jako że prędkość to pierwsza pochodna położenia, przyspieszenie można określić jako drugą pochodną tego położenia. Ta kluczowa zależność odnosi się do kinematyki i umożliwia nam analizę ruchu obiektów poprzez funkcje opisujące ich położenie. Warto zauważyć, że zmiany prędkości w czasie bezpośrednio wpływają na przyspieszenie, które z kolei pokazuje, jak szybko te zmiany mają miejsce.

Jak obliczyć przyspieszenie w praktyce?

Obliczanie przyspieszenia w praktyce polega na pomiarze początkowej oraz końcowej prędkości, a także czasu, w którym następuje ta zmiana. Przyspieszenie (a) obliczamy za pomocą wzoru: a = ΔV / Δt. Tutaj ΔV oznacza różnicę między prędkością końcową a początkową, natomiast Δt to czas, w którym ta zmiana zachodzi.

Na przykład, wyobraźmy sobie, że samochód przyspiesza od stanu spoczynku do 20 m/s w ciągu 5 sekund. W takim przypadku przeliczenie przyspieszenia będzie wyglądało następująco: (20 m/s – 0 m/s) / 5 s = 4 m/s². Taki sposób obliczania umożliwia analizę różnorodnych ruchów, zarówno prostoliniowych, jak i zakrzywionych, na podstawie prostych i łatwych do wykonania pomiarów.

Dodatkowo w kinematyce oraz dynamice ta metoda odgrywa kluczową rolę w opisie i przewidywaniu zmian prędkości w czasie.

Podstawowe przykłady obliczeń

Przykład obliczania przyspieszenia ilustruje sytuację, w której samochód zmienia swoją prędkość. Mając na uwadze prędkość początkową i końcową oraz czas Δt, który był konieczny do tej zmiany, można łatwo wyznaczyć średnie przyspieszenie. Używamy do tego wzoru a = Δv / Δt, gdzie Δv to różnica pomiędzy prędkością końcową a początkową.

Na przykład, jeśli samochód przyspiesza od 20 m/s do 30 m/s w czasie 5 sekund, kalkulacja przyspieszenia wyglądałaby następująco: (30 m/s – 20 m/s) / 5 s, co daje 2 m/s².

Takie obliczenia są niezwykle przydatne do analizy ruchu, czy to jednostajnie przyspieszonego, czy opóźnionego. Dodatkowo w praktyce często korzysta się z bardziej złożonych równań ruchu, które umożliwiają dokładniejsze śledzenie zmian prędkości w czasie.

Zmiana prędkości – od prędkości początkowej do końcowej

Zmiana prędkości, znana jako (ΔV), to różnica pomiędzy prędkością końcową (V_k) a prędkością początkową (V_p). Można to ująć w prostym równaniu: ΔV = V_k – V_p. Ta wartość odgrywa istotną rolę w obliczeniach związanych z średnim przyspieszeniem.

Warto zauważyć, że zmiana prędkości dotyczy zarówno wartości, jak i kierunku wektora prędkości, co w znaczący sposób wpływa na dynamikę ruchu obiektu. Na przykład, gdy obiekt zmienia kierunek, jego ruch staje się bardziej złożony. Dodatkowo, uwzględniając zarówno prędkość początkową, jak i końcową, możemy precyzyjniej określić:

• jak szybko zachodzi zmiana prędkości,
• w jaki sposób zmienia się ruch,
• jakie czynniki wpływają na te zmiany.

Jakie są rodzaje przyspieszenia?

Przyspieszenie można podzielić na kilka podstawowych typów, które przedstawiają różne aspekty zmiany prędkości w ruchu.

• Przyspieszenie średnie odnosi się do zmiany prędkości na jednostkę czasu w określonym przedziale,
• Przyspieszenie chwilowe to momentalne odzwierciedlenie przyspieszenia średniego, gdy czas dąży do zera,
• przyspieszenie chwilowe informuje nas o tym, jak szybko zmienia się prędkość w danym ułamku sekundy.

W kontekście ruchu krzywoliniowego możemy wyróżnić dwa główne typy przyspieszenia:

• Przyspieszenie styczne wpływa bezpośrednio na wartość prędkości, co pozwala na przyspieszenie lub spowolnienie ruchu,
• Przyspieszenie normalne, często nazywane dośrodkowym, zmienia kierunek prędkości,
• umożliwia to ciału podążanie po zakrzywionej ścieżce, jak w przypadku ruchu po okręgu.

W ruchu obrotowym mamy do czynienia z przyspieszeniem kątowym, które określa, jak zmienia się prędkość kątowa obiektu. Ta miara wskazuje tempo, w jakim przekształca się kąt obrotu w czasie.

Zrozumienie tych różnorodnych rodzajów przyspieszenia jest niezbędne do analizy ruchu, zarówno w kinematyce, jak i dynamice.

Przyspieszenie średnie

Przyspieszenie średnie to wskaźnik, który określa, jak bardzo zmienia się prędkość (ΔV) w odniesieniu do czasu, w którym ta zmiana następuje (Δt). Oblicza się je według wzoru: a = ΔV / Δt. Ta wartość przedstawia ogólne przyspieszenie w określonym przedziale czasowym, co umożliwia analizę zmian prędkości w ruchu, który nie jest stały.

Warto jednak pamiętać, że przyspieszenie średnie nie uwzględnia szczegółowych fluktuacji prędkości, które mogą wystąpić w krótszych okresach. Zamiast tego dostarcza tylko wartość uśrednioną dla całego badanego czasu. To jest kluczowe, ponieważ pozwala na wyliczenie przyspieszenia chwilowego, które opisuje sytuację w konkretnym momencie.

Na przykład, przyspieszenie średnie jest niezwykle istotne w sytuacjach, gdy prędkość rośnie stopniowo, jak w przypadku ruchu jednostajnie przyspieszonego. Ponadto zrozumienie tego terminu sprawia, że łatwiej analizujemy różne zjawiska ruchu w fisyce.

Przyspieszenie chwilowe

Przyspieszenie chwilowe można zdefiniować jako granicę średniego przyspieszenia w momencie, gdy interwał czasowy Δt dąży do zera. Można je traktować jako pochodną prędkości względem czasu, co oznacza, że wskazuje, w jakim tempie prędkość zmienia się w danej chwili.

Na wykresie, gdzie prędkość jest przedstawiona w odniesieniu do czasu, przyspieszenie chwilowe odpowiada nachyleniu stycznej do krzywej prędkości. Dzięki temu narzędziu możemy precyzyjnie zobaczyć, jak zmienia się prędkość w wybranym punkcie czasowym. Zrozumienie tego zjawiska odgrywa kluczową rolę w analizie ruchu.

Przyspieszenie styczne i normalne

Przyspieszenie styczne to ta część przyspieszenia, która działa równolegle do toru ruchu, a więc to ono odpowiada za zmiany prędkości obiektu poruszającego się po krzywej. Przyspieszenie normalne, nazywane także przyspieszeniem dośrodkowym, działa w kierunku prostopadłym do toru, zmieniając kierunek prędkości.

W kontekście ruchu krzywoliniowego, całkowite przyspieszenie ciała można zobrazować jako wektor, wynikający z sumy przyspieszenia stycznego i normalnego. Przyspieszenie dośrodkowe stanowi szczególny przypadek przyspieszenia normalnego, zawsze skierowane w stronę środka krzywizny toru.

Te dwa elementy są niezwykle istotne dla zrozumienia dynamiki ruchu po zakręcie. Co więcej, mają one znaczący wpływ na różne aspekty zmiany prędkości podczas ruchu po krzywej.

Przyspieszenie dośrodkowe

Przyspieszenie dośrodkowe, znane również jako przyspieszenie normalne, to szczególny rodzaj przyspieszenia, które działa prostopadle do kierunku, w którym porusza się obiekt. Można je zaobserwować podczas ruchu po okręgu lub innej krzywej, ponieważ odpowiada za zmianę kierunku prędkości, nie wpływając jednocześnie na jej wartość.

To przyspieszenie zawsze zmierza w stronę środka zakrzywionej trasy, co powoduje, że ścieżka ruchu nieustannie „zakrzywia” się. Dzięki temu obiekt przemieszczający się po okręgu pozostaje na krzywoliniowej trajektorii, nawet gdy jego prędkość pozostaje niezmieniona.

Wszystko to sprawia, że przyspieszenie dośrodkowe odgrywa istotną rolę w analizie ruchu po okręgu. Bez tej czynności, obiekt nie miałby możliwości utrzymania się na tej właśnie ścieżce.

Przyspieszenie kątowe

Przyspieszenie kątowe to wskaźnik, który określa, jak szybko zmienia się prędkość kątowa obiektu obracającego się wokół osi. Jest to wektor, potocznie nazywany pseudowektorem, a jego kierunek można ustalić, stosując regułę prawej śruby. Jednostką przyspieszenia kątowego są radiany na sekundę do kwadratu (rad/s²).

Działa ono na zasadzie analogicznej do przyspieszenia liniowego, ale dotyczy ruchu obrotowego. Innymi słowy, przyspieszenie kątowe mówi nam, jak szybko dochodzi do zmiany prędkości kątowej danego obiektu.

Jakie są jednostki przyspieszenia?

Jednostką przyspieszenia w układzie SI jest metr na sekundę do kwadratu, czyli m/s². Ta jednostka opisuje, w jaki sposób prędkość zmienia się, osiągając wzrost o 1 metr na sekundę w każdej sekundzie. Metry na sekundę kwadrat to powszechnie stosowana jednostka w dziedzinach takich jak fizyka i inżynieria.

Choć można spotkać inne jednostki przyspieszenia, są one rzadziej używane i zazwyczaj trzeba je przeliczać na jednostki SI. Takie przeliczenia zapewniają:

• spójność w pomiarach,
• spójność w obliczeniach,
• uproszenie opisu tempa zmiany prędkości w różnych kontekstach.

Przykłady kontekstów to analiza ruchu prostoliniowego oraz dynamika obiektów.

Jednostka SI: metr na sekundę kwadrat (m/s²)

Metr na sekundę kwadrat (m/s²) to standardowa jednostka miary przyspieszenia w systemie SI. W praktyce oznacza to, że prędkość obiektu zmienia się o 1 metr na sekundę w każdej upływającej sekundzie. Ta miara ukazuje, jak szybko prędkość obiektu reaguje na upływ czasu. Znajduje zastosowanie zarówno w przypadku ruchu prostoliniowego, jak i w dynamicznych zjawiskach obrotowych.

W świecie fizyki oraz inżynierii, jednostka m/s² jest niezwykle użyteczna, umożliwiając analizę ruchu obiektów i sił działających na nie. Dzięki pomiarom wyrażonym w metrach na sekundę do kwadratu można precyzyjnie określić, w jakim tempie obiekty przyspieszają lub zwalniają, co jest kluczowe w wielu zastosowaniach praktycznych.

Inne jednostki i przeliczanie

Wśród różnych jednostek przyspieszenia, obok metra na sekundę kwadrat (m/s²), znajdziemy również stopę na sekundę kwadrat (ft/s²), która należy do systemu imperialnego. Żeby przeliczyć te jednostki na siebie, musimy zastosować odpowiednie współczynniki konwersji. Na przykład, jeden ft/s² przekłada się na około 0,3048 m/s².

Mimo to, najczęściej używaną oraz zalecaną jednostką pozostaje m/s². Jej popularność wynika z wszechstronności i powszechnego zastosowania w dziedzinach nauki oraz techniki. Dokładne przeliczanie jednostek przyspieszenia ma kluczowe znaczenie, zwłaszcza w kontekście analizy ruchu i obliczeń inżynieryjnych.

Jakie znaczenie ma przyspieszenie w kinematyce i dynamice?

Przyspieszenie to fundamentalny koncept zarówno w kinematyce, jak i dynamice. W kinematyce umożliwia nam opisanie, w jaki sposób prędkość obiektów ulega zmianie, dzięki czemu możemy dogłębnie analizować różnorodne aspekty ruchu. Przyspieszenie informuje nas o szybkości oraz kierunku, w jakim następują te zmiany prędkości.

Z kolei w dynamice przyspieszenie jest ściśle związane z działającymi na ciało siłami. Zgodnie z drugą zasadą dynamiki Newtona, która można zapisać jako a = F/m, przyspieszenie ciała jest proporcjonalne do siły działającej na nie i odwrotnie proporcjonalne do jego masy.

Dzięki temu równaniu mamy możliwość prognozowania ruchu obiektów, gdy tylko znamy ich masy oraz działające na nie siły. To jest kluczowy element analizy dynamicznej w fizyce. Można powiedzieć, że przyspieszenie splata ze sobą siły i zmiany ruchu, co pozwala na skuteczne modelowanie oraz zrozumienie mechaniki ruchu.

Druga zasada dynamiki Newtona: a = F/m

Druga zasada dynamiki Newtona opisuje zależność między siłą a przyspieszeniem ciała. Sformułowanie a = F/m wskazuje, że przyspieszenie (a) można obliczyć, dzieląc całkowitą siłę (F) działającą na dany obiekt przez jego masę (m).

Oznacza to, że:

• jeśli na obiekt z określoną masą działa większa siła, przyspieszenie wzrośnie,
• samochód o stałej masie przyspieszy mocniej, gdy zastosujemy na niego większą siłę,
• im większa masa ciała, tym wolniejsze będzie jego przyspieszenie, gdy zastosujemy tę samą siłę.

Ta zasada jest fundamentalna w dziedzinie dynamiki, gdyż umożliwia prognozowanie ruchu obiektów pod wpływem różnych sił. Dzięki niej możemy obliczyć przyspieszenie, mając informacje o sile oraz masie. Jest to narzędzie, które pozwala lepiej zrozumieć, w jaki sposób różnorodne siły wpływają na ruch w naszym codziennym życiu.

Związek siły, masy i przyspieszenia

Związek między siłą, masą a przyspieszeniem jest kluczowym elementem drugiej zasady dynamiki Newtona, wyrażonej równaniem F = ma. Siła (F), która działa na ciało o określonej masie (m), wpływa na jego przyspieszenie (a). Przyspieszenie to jest wprost proporcjonalne do aplikowanej siły, natomiast odwrotnie proporcjonalne do masy obiektu.

Innymi słowy, im większa siła jest wywierana na dany obiekt, tym wyższe będzie osiągane przyspieszenie. Z drugiej jednak strony, większa masa danego ciała prowadzi do mniejszego przyspieszenia w przypadku tej samej siły.

Zrozumienie tego fundamentalnego związku jest niezwykle istotne, ponieważ pozwala nam analizować ruch różnych przedmiotów. Dzięki tej wiedzy jesteśmy w stanie przewidywać, jak zmienia się ich prędkość i kierunek ruchu pod wpływem różnych sił działających na nie.

Czym różni się przyspieszenie dodatnie od opóźnienia?

Przyspieszenie dodatnie to sytuacja, w której prędkość obiektu zwiększa się w określonym kierunku, co oznacza, że porusza się on coraz szybciej. Opóźnienie, które jest formą ujemnego przyspieszenia, wskazuje na redukcję prędkości — czyli spowolnienie ruchu.

Choć oba zjawiska są typami przyspieszenia, różnią się one swoim znakiem. Dodatnie przyspieszenie ma miejsce, gdy obiekt przyspiesza, natomiast opóźnienie występuje, gdy następuje hamowanie lub zwalnianie. W przypadku ruchu przyspieszonego prędkość rośnie, natomiast w ruchu opóźnionym maleje.

Jak przyspieszenie występuje w ruchu po linii prostej i po okręgu?

W ruchu prostoliniowym przyspieszenie działa wzdłuż ścieżki, co prowadzi do zmiany prędkości, ale nie wpływa na jej kierunek ani zwrot. Krótko mówiąc, przyspieszenie styczne sprawia, że obiekt poruszający się po linii prostej może albo zwiększać swoją prędkość, albo zwalniać.

Z kolei w ruchu po okręgu przyspieszenie składa się z dwóch elementów:

• przyspieszenie styczne, które zmienia wartość prędkości – może ją zarówno podnosić, jak i obniżać,
• przyspieszenie dośrodkowe, działające pod kątem do kierunku prędkości i skierowane w stronę środka okręgu.

Ta forma przyspieszenia jest odpowiedzialna za zmianę kierunku prędkości, co umożliwia obiektowi poruszanie się po krzywej zamiast po prostej linii.

Przyspieszenie dośrodkowe odgrywa kluczową rolę w utrzymaniu obiektu na torze okręgu. Można je obliczyć za pomocą wzoru a = v²/r, gdzie v oznacza prędkość, a r to promień okręgu. Dzięki współdziałaniu przyspieszenia stycznego i dośrodkowego, obiekt zyskuje możliwość zmiany zarówno swojej szybkości, jak i kierunku ruchu podczas podróży po okrągłej trasie.

Jak przyspieszenie ilustruje ruch jednostajnie przyspieszony i opóźniony?

Ruch jednostajnie przyspieszony to zjawisko, w którym przyspieszenie pozostaje na stałym poziomie, co prowadzi do systematycznego wzrostu prędkości obiektu. Aby obliczyć prędkość końcową \(v_k\) w takim ruchu, możemy zastosować wzór:

\[v_k = v_0 + at\]

Tutaj:

• v_0 oznacza prędkość początkową,
• a to wartość przyspieszenia,
• t to czas trwania ruchu.

Ruch jednostajnie opóźniony charakteryzuje się stałym, ale ujemnym przyspieszeniem, co skutkuje stopniowym malejącym tempem obiektu aż do momentu całkowitego zatrzymania.

Obie te formy ruchu pokazują, w jaki sposób przyspieszenie oddziałuje na prędkość w czasie. Dzięki tym zjawiskom możemy precyzyjnie obliczyć położenie oraz prędkość obiektu w funkcji czasu, wykorzystując odpowiednie równania ruchu jednostajnie przyspieszonego.

Równania ruchu jednostajnie przyspieszonego

Równania ruchu jednostajnie przyspieszonego pomagają zrozumieć, jak zmieniają się prędkość oraz droga obiektu poruszającego się z stałym przyspieszeniem. Kluczowym wzorem opisującym prędkość końcową jest: v = v0 + at. W tym równaniu v0 reprezentuje prędkość początkową, natomiast a to stałe przyspieszenie.

Droga, jaką przebywa ciało w danym czasie t, określa się za pomocą wzoru: s = v0 t + 0,5 a t². Gdy chcemy obliczyć przyspieszenie, korzystamy z formuły: a = Δv/Δt, co oznacza zmianę prędkości w określonym okresie.

Dzięki tym równaniom możemy precyzyjnie analizować różne aspekty ruchu jednostajnie przyspieszonego, takie jak:

• prędkość w konkretnym momencie,
• przebyta droga.

Owe wzory są nieocenione w kinematyce i służą do opisywania ruchów pojazdów, swobodnych spadków czy innych sytuacji, gdzie prędkość zmienia się liniowo w funkcji czasu.

Jak mierzyć przyspieszenie?

Pomiar przyspieszenia zazwyczaj dokonuje się przy użyciu akcelerometrów — specjalistycznych urządzeń, które przetwarzają zmiany w przyspieszeniu. Te narzędzia rejestrują zmiany prędkości w czasie, co skutkuje precyzyjnym odczytem przyspieszenia, niezależnie od tego, czy mamy do czynienia z warunkami statycznymi, czy dynamicznymi.

Innym sposobem na określenie przyspieszenia jest analiza wykresów prędkości. Tutaj, zmiany prędkości w czasie pozwalają na wyliczenie wartości przyspieszenia, korzystając z kinematycznych wzorów, takich jak a = Δv/Δt. Dzięki tym równaniom można łatwo ustalić przyspieszenie, analizując prędkości początkową i końcową, a także czas, w którym te zmiany zachodziły.

Akcelerometry są szeroko wykorzystywane w różnych dziedzinach, takich jak:

• przemysł motoryzacyjny, gdzie odgrywają kluczową rolę w mierzeniu przyspieszenia pojazdów,
• elektronika użytkowa, na przykład w smartfonach,
• badania naukowe, gdzie ich precyzja i szybkość pomiarów są nieocenione.

Dzięki akcelerometrom możemy dokładnie badać ruch ciał, co otwiera nowe możliwości w różnych dziedzinach.

Akcelerometr i metody pomiaru

Akcelerometr to urządzenie, które służy do pomiaru przyspieszenia obiektów. Jego działanie opiera się na wykrywaniu sił bezwładności, które oddziałują na wewnętrzne komponenty. Po zarejestrowaniu tych sił, przekształcają je w impulsy elektryczne, które można potem analizować w celu określenia wartości przyspieszenia.

Inna metoda pomiaru przyspieszenia korzysta z obliczeń matematycznych, posługując się równaniem a = Δv/Δt. To proste wyrażenie określa, jak zmienia się prędkość w określonym czasie. Również analiza wykresów prędkości może dostarczyć istotnych informacji — nachylenie krzywej na wykresie jednoznacznie wskazuje, jak szybko następuje przyspieszenie.

Akcelerometry znajdują zastosowanie w wielu dziedzinach:

• na nawigacji,
• w badaniach ruchu,
• w systemach bezpieczeństwa,
• zastosowanie w urzędzeniach mobilnych,
• w grach komputerowych.

Co więcej, ich rozwój przyczynia się do rewolucji technologicznej w różnych branżach.

Czym jest przyspieszenie grawitacyjne i przyspieszenie ziemskie?

Przyspieszenie grawitacyjne to siła, jaką grawitacja działa na obiekty. Kiedy mówimy o powierzchni Ziemi, zjawisko to określamy jako przyspieszenie ziemskie, które wynosi około 9,81 m/s². To istotny parametr, gdy analizujemy ruch swobodnego spadku, w którym obiekt porusza się wyłącznie dzięki grawitacji, bez oddziaływania oporu powietrza.

Choć na różnych szerokościach geograficznych wartość ta może się nieznacznie różnić, w przyjętej średniej wynosi ona 9,81 m/s². Dlatego właśnie te parametry odgrywają kluczową rolę w fizyce i inżynierii, szczególnie w kontekście obliczeń dotyczących ruchu ciał w polu grawitacyjnym.

Jakie są zastosowania wzoru na przyspieszenie w codziennym życiu?

Wzór na przyspieszenie a = Δv/Δt ma praktyczne zastosowanie w wielu aspektach codziennego życia. Na przykład, w przypadku pojazdów, takich jak samochody, umożliwia obliczanie, jak szybko zmienia się ich prędkość podczas przyspieszania lub hamowania. To z kolei wpływa na bezpieczeństwo na drodze oraz na reakcje kierowców w różnych sytuacjach.

W dziedzinie inżynierii ruchu drogowego wykorzystuje się ten wzór do:

• projektowania skutecznych systemów hamowania,
• monitorowania prędkości,
• oceny jakości dróg,
• analizy zachowań kierowców,
• planowania nowych rozwiązań transportowych.

Oprócz tego, jest on istotny w badaniach dotyczących swobodnego spadku ciał, gdyż opisuje przyspieszenie ziemskie wynoszące około 9,81 m/s².

Dzięki tym danym można oszacować czas, jaki zajmuje obiektom opadnięcie oraz ich końcową prędkość. Tego rodzaju wiedza jest niezbędna zarówno w nauce, jak i w wielu zastosowaniach technicznych. W ten sposób wzór na przyspieszenie odgrywa kluczową rolę w:

• zapewnieniu bezpieczeństwa,
• planowaniu ruchu,
• zrozumieniu fizycznych fenomenów występujących w naszym otoczeniu.

Samochód i ruch pojazdów

Przyspieszenie pojazdu to kluczowy wskaźnik, który określa, jak szybko zmienia się jego prędkość, gdy rozpędza się lub zwalnia. Można je wyliczyć za pomocą prostego wzoru a = Δv/Δt, gdzie Δv oznacza różnicę prędkości, a Δt to czas, w którym ta zmiana następuje. Dzięki tym obliczeniom uzyskujemy cenny wgląd w dynamikę pojazdu, np. analizując przyspieszenie z 0 do 100 km/h. To informacje, które są nieocenione, gdy mowa o bezpieczeństwie jazdy oraz wydajności silnika.

W praktyce wyróżniamy dwa rodzaje przyspieszenia:

• średnie, które mierzymy na określonym fragmencie czasu,
• chwilowe, odnoszące się do konkretnego momentu ruchu.

Zrozumienie pojęcia przyspieszenia jest nie tylko ważne podczas projektowania samochodów, ale również w rozwijaniu umiejętności prowadzenia pojazdu. Co więcej, znajomość tego aspektu może znacząco przyczynić się do zwiększenia bezpieczeństwa na drogach.

Swobodny spadek

Swobodny spadek to zjawisko, które polega na ruchu obiektu, wywołanym przez przyspieszenie grawitacyjne. Dzieje się tak, gdy nie ma żadnego oporu ze strony powietrza. Przyspieszenie w tym przypadku wynosi około 9,81 m/s², co odpowiada przyciąganiu ziemskiemu.

Aby lepiej zrozumieć swobodny spadek, korzystamy z równań opisujących ruch jednostajnie przyspieszony. Dzięki tym matematycznym zależnościom możemy obliczyć zarówno:

• prędkość,
• drogę,
• czas spadania,
• siłę grawitacji,
• wpływ masy na ruch.

Ten rodzaj ruchu wyraźnie ilustruje działanie siły grawitacji na każdy spadający przedmiot.