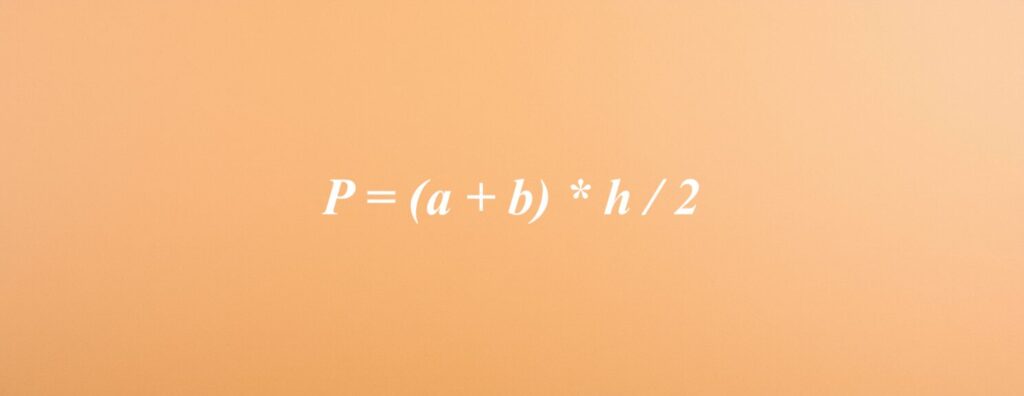Trapez równoramienny: definicja i własności
Trapez równoramienny to wyjątkowy rodzaj trapezu, charakteryzujący się kilkoma unikalnymi właściwościami. Jego szczególną cechą są dwie równoległe podstawy oraz boki o tej samej długości, co odróżnia go od innych typów trapezów. Kąty przy tych podstawach są sobie równe, co nadaje mu symetrię i wpływa na estetyczny wygląd figury.
Kolejnym interesującym aspektem trapezu równoramiennego jest fakt, że jego przekątne mają identyczną długość. Oznacza to, że linie łączące przeciwległe wierzchołki są równe. Co więcej, suma kątów przy różnych podstawach wynosi zawsze 180 stopni.
Wysokość tego rodzaju trapezu jest prostopadła do jego podstaw i łatwa do wyznaczenia dzięki harmonijnemu układowi boków oraz kątów. Linia środkowa pełni istotną rolę – jej długość odpowiada połowie sumy obu podstaw. Dzięki tym właściwościom trapez równoramienny jest często analizowany w geometrii oraz stosowany praktycznie, na przykład w projektowaniu konstrukcji architektonicznych.
Wzór na pole trapezu równoramiennego
Aby obliczyć pole trapezu równoramiennego, można skorzystać z formuły: P = (a + b) * h / 2. W tym przypadku a i b to długości podstaw, natomiast h oznacza wysokość, czyli odległość dzielącą te podstawy. Alternatywnie, dla trapezu równoramiennego dostępny jest jeszcze inny sposób: P = 1/2 * e^2 * sin(β). Tutaj e to długość ramion, a β symbolizuje kąt przy jednej z podstaw. Obie metody umożliwiają precyzyjne wyznaczenie pola tego rodzaju trapezu.
Jak obliczyć pole trapezu równoramiennego?
Aby obliczyć pole trapezu równoramiennego, możemy zastosować następujące wzory:
- P = (a + b) * h / 2, gdzie a i b oznaczają długości podstaw, a h jest wysokością,
- w przypadku, gdy dysponujemy długościami ramion e oraz kątem β przy podstawie, dostępny jest wzór P = 1/2 * e^2 * sin(β).
Kluczowe jest precyzyjne określenie potrzebnych wartości przed rozpoczęciem obliczeń, aby wynik był wyrażony w odpowiednich jednostkach kwadratowych.
Podstawy trapezu i ich suma długości
Podstawy trapezu równoramiennego to dwa boki, które są do siebie równoległe i oznaczamy je jako a i b. Ich suma odgrywa kluczową rolę przy wyliczaniu pola tej figury.
Aby obliczyć pole trapezu równoramiennego, używamy wzoru: P = 1/2 * (a + b) * h. Suma długości tych podstaw jest istotna, ponieważ mnożymy ją przez wysokość h, a wynik dzielimy przez 2, by uzyskać pole trapezu.
W ten sposób dostrzegamy znaczenie podstaw w geometrii trapezu oraz ich wpływ na wynik obliczeń powierzchni tej figury geometrycznej.
Kąty przy podstawie i ich wpływ na pole
Kąty przy podstawie trapezu równoramiennego mają identyczne miary, co przyczynia się do symetrii tej figury, choć bezpośrednio nie wpływa na obliczanie pola. Pole trapezu zależy głównie od długości jego podstaw i wysokości. Mimo to te kąty mogą okazać się istotne w innych obliczeniach, jak określanie długości ramion czy wysokości. Na przykład, wartość tych kątów może mieć wpływ na orientację oraz geometrię trapezu. Znajomość miar kątów umożliwia dokładniejsze określenie właściwości trapezu w kontekście specyficznych zadań geometrycznych.
Wysokość trapezu: jak ją znaleźć?
Wysokość trapezu można określić na wiele sposobów, korzystając z dostępnych danych. Do najczęściej wykorzystywanych metod należą modyfikacja wzoru na pole oraz zastosowanie twierdzenia Pitagorasa.
- kiedy dysponujesz informacjami o polu trapezu i długościach jego podstaw, wysokość obliczysz, przekształcając wzór na pole,
- dla pola P i sumy długości podstaw S stosujemy formułę: \( h = \frac{2P}{S} \),
- przykładowo, gdy pole wynosi 24 cm², a suma podstaw to 12 cm, wtedy wysokość będzie równa \( h = \frac{48}{12} = 4 \) cm.
Alternatywnie można skorzystać z twierdzenia Pitagorasa. Znając długości ramion i jednej z podstaw, wysokość wyznacza się za pomocą równań geometrycznych w trójkątach prostokątnych utworzonych przez tę wysokość. W przypadku trapezów równoramiennych dodatkowe informacje o kątach przy podstawach mogą być również przydatne do wykorzystania funkcji trygonometrycznych w celu ustalenia brakującej wysokości.
Przykłady obliczeń pola trapezu równoramiennego
Przykładowe zadania z obliczaniem powierzchni trapezu równoramiennego pokazują, jak używać odpowiednich wzorów w praktyce. Załóżmy, że długości podstaw wynoszą: a = 6 cm i b = 4 cm, podczas gdy wysokość to 5 cm. Pole tego trapezu można znaleźć za pomocą wzoru: P = 1/2 * (6 + 4) * 5, co daje nam wynik 25 cm².
W innym scenariuszu, gdzie a równa się 8 cm, b to 6 cm, a wysokość to zaledwie 3 cm, obliczamy pole jako P = 1/2 * (8 + 6) * 3 i otrzymujemy wartość 21 cm².
Istnieją również inne zadania do rozwiązania, takie jak sytuacja z znanym tangensem kąta ostrego oraz długościami podstawy i ramienia. Jeśli przykładowo podstawy mają długości a = 5 oraz b = 13, a tangens kąta ostrego wynosi tan(θ) = 2, trygonometria może pomóc w określeniu wysokości i dalszym wyznaczeniu pola.
Te przykłady ukazują różne podejścia do rozwiązywania problemów związanych z trapezem równoramiennym i demonstrują praktyczne wykorzystanie wzorów matematycznych w geometrii.