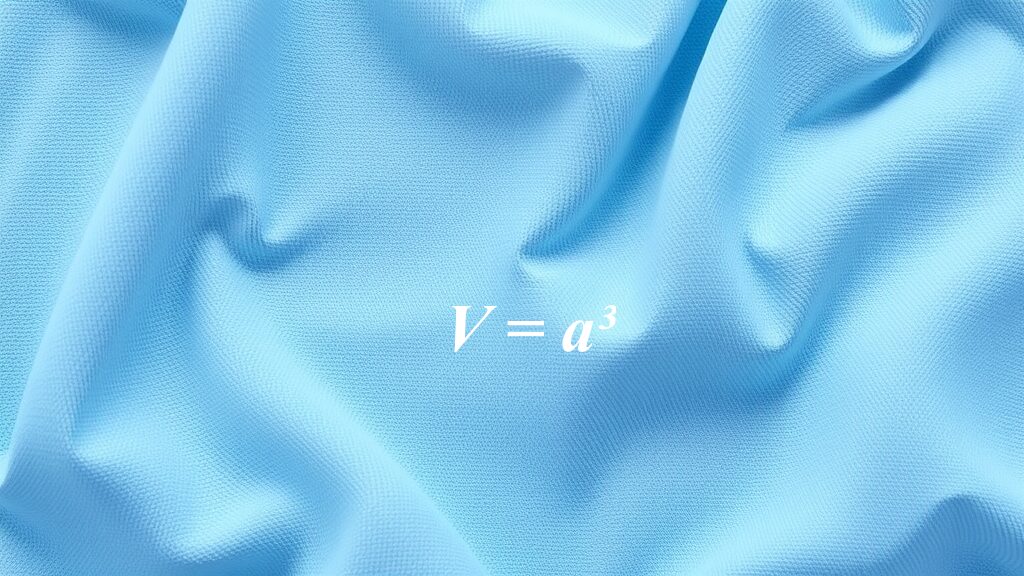Wzór na objętość sześcianu

Sześcian to trójwymiarowa figura geometryczna, która ma istotne znaczenie w geometrii oraz stereometrii. Stanowi on szczególny typ prostopadłościanu oraz graniastosłupa, składając się z sześciu identycznych ścian w formie kwadratów. Co interesujące, długości wszystkich krawędzi sześcianu są równe, co nadaje mu charakterystyczną symetrię i regularność.

Figurę tę cechuje wiele interesujących właściwości:

dwanaście krawędzi,
osiem wierzchołków,
sześć ścian.

Warto także zaznaczyć, że znajduje on zastosowanie w różnych dziedzinach, w tym matematyce, inżynierii oraz architekturze. Jego prostota oraz regularność są niezwykle cenne w tych obszarach.

Sześcian można spotkać w różnych kontekstach – od edukacyjnych zabawek po bardziej złożone modele architektoniczne. Dzięki swoim unikalnym cechom jest nie tylko ciekawym obiektem badań w naukach o przestrzeni, ale także funkcjonalnym elementem w projektowaniu różnorodnych konstrukcji.

Jakie cechy posiada sześcian?

Sześcian to figura geometryczna o niezwykłych cechach. Każdy z jego boków ma tę samą długość, co oznacza, że krawędzie sześcianu są równe. Wszystkie sześć ścian ma formę kwadratów o identycznych wymiarach, co nadaje sześcianowi imponującą symetrię i regularność.

Dodatkowo, sześcian składa się z:

12 krawędzi,
8 wierzchołków.

Te cechy sprawiają, że analiza sześcianu w kontekście obliczeń geometrycznych jest znacznie łatwiejsza. Dzięki swojej regularności, wszystkie krawędzie są identyczne, co upraszcza wszelkie obliczenia. Te unikalne właściwości czynią sześcian istotnym elementem w dziedzinach takich jak matematyka, inżynieria czy architektura.

Ile ścian, krawędzi i wierzchołków ma sześcian?

Sześcian to niezwykle ważna bryła przestrzenna, którą można łatwo zidentyfikować dzięki jej unikalnym cechom. Posiada:

sześć identycznych ścian w kształcie kwadratów,
dwanaście krawędzi, z których każda ma identyczną długość,
osiem wierzchołków, w których łączą się krawędzie.

Te charakterystyki sprawiają, że sześcian jest nie tylko rozpoznawalny, ale również często wykorzystywany w geometrii i matematyce.

Krawędzie sześcianu odgrywają kluczową rolę w obliczeniach dotyczących jego objętości oraz powierzchni. Łączna długość wszystkich krawędzi wynosi dwanaście razy długość jednej z nich. Wiedza na temat liczby ścian, krawędzi i wierzchołków jest niezbędna w różnych obliczeniach matematycznych, a także staje się istotna w zastosowaniach architektonicznych i inżynieryjnych.

Jak wygląda wzór na objętość sześcianu?

Wzór na obliczenie objętości sześcianu to V = a³, gdzie „a” to długość jego krawędzi. Aby znaleźć objętość, wystarczy potęgować długość boku, co oznacza, że mnożymy długość każdej krawędzi przez siebie trzy razy. W ten sposób uzyskujemy objętość wewnętrzną tej bryły.

Objętość sześcianu, podawana w jednostkach sześciennych, informuje nas o całkowitej przestrzeni, jaką zajmuje. Formuła V = a³ jest nie tylko praktyczna, ale również łatwa do zapamiętania, co sprawia, że obliczenia związane z sześcianem są przystępne dla uczniów i studentów. Kluczowym etapem jest potęgowanie długości krawędzi, ponieważ sześcian to szczególny przypadek prostopadłościanu, w którym wszystkie krawędzie mają tę samą długość.

Zastosowanie tego wzoru jest niezwykle istotne zarówno w matematyce, jak i w różnych dziedzinach inżynieryjnych. Gdy dokładne obliczenia objętości mają ogromne znaczenie, umiejętność posługiwania się tym wzorem okazuje się nieoceniona. Zrozumienie sposobu, w jaki działa ta formuła oraz jej zastosowań, pozwala lepiej pojąć trójwymiarowe bryły i ich rolę w praktycznych sytuacjach.

Dlaczego stosuje się wzór V = a³?

Wzór V = a³ jest wykorzystywany z uwagi na charakterystykę sześcianu. W tym kształcie wszystkie krawędzie mają identyczną długość, co upraszcza proces obliczania objętości. Aby obliczyć objętość sześcianu, wystarczy podnieść długość jednej z krawędzi do potęgi trzeciej. Dzięki temu unikamy skomplikowanego mnożenia różnych wymiarów, co ma miejsce w przypadku prostopadłościanów.

Kiedy korzystamy z wzoru V = a³, szybko zyskujemy pożądane rezultaty. Takie ułatwienie ma duże znaczenie zarówno w edukacji, jak i w zastosowaniach inżynieryjnych czy architektonicznych. Dzięki niemu można błyskawicznie obliczyć objętość oraz przeprowadzić analizy przestrzenne, co jest niezbędne przy projektowaniu budynków, mebli czy innych struktur, gdzie sześciany są powszechnie stosowane.

Korzyści płynące z wykorzystania wzoru V = a³ to:

prosta metoda obliczeń,
szybkie rezultaty,
precyzyjne wyniki,
łatwość w zastosowaniach inżynieryjnych,
praktyczność w edukacji.

Również prowadzą do precyzyjnych wyników, co jest kluczowe w wielu obszarach matematyki i inżynierii.

Jak interpretować wzór na objętość sześcianu?

Wzór na objętość sześcianu, V = a³, stanowi kluczowy element geometrii przestrzennej. Dzięki niemu możemy efektywnie obliczyć, jaką przestrzeń zajmuje sześcian. W równaniu tym „a” oznacza długość krawędzi, podczas gdy „V” reprezentuje objętość, wyrażoną w jednostkach sześciennych, takich jak cm³ czy m³.

Zrozumienie V = a³ jest niezbędne do poprawnego obliczania objętości sześcianów. W praktyce, wystarczy pomnożyć długość krawędzi przez siebie trzy razy. Na przykład, dla sześcianu o krawędzi wynoszącej 2 cm, obliczenia wyglądają następująco:

2 cm × 2 cm × 2 cm,
co daje wynik 8 cm³.

Objętość sześcianu odzwierciedla ilość przestrzeni zamkniętej w jego wnętrzu. Można ją również podać w decymetrach sześciennych (dm³), co znacznie ułatwia porównywanie różnych obiektów oraz przeprowadzanie obliczeń w dziedzinach matematyki czy inżynierii. Zrozumienie i umiejętność stosowania tego wzoru to niezbędna wiedza dla każdego ucznia geometrii oraz osób zajmujących się projektowaniem obiektów przestrzennych.

Jak obliczyć objętość sześcianu krok po kroku?

Aby obliczyć objętość sześcianu, wykonaj kilka prostych kroków.

Zacznij od zmierzenia długości krawędzi sześcianu, oznaczanej literą „a”. To właśnie ten wymiar jest kluczowy dla naszego obliczenia. Załóżmy, że krawędź ma długość 5 cm.

Teraz możesz skorzystać z formuły na objętość sześcianu: V = a³. W naszym przypadku obliczenia będą wyglądać następująco:

V = 5 cm × 5 cm × 5 cm, co można także zapisać jako V = 5³. Po dokonaniu mnożenia otrzymujesz V = 125 cm³.

Uzyskany wynik powinien być wyrażony w jednostkach objętości, takich jak:

centymetry sześcienne (cm³),
metry sześcienne (m³).

Na przykład, dla długości krawędzi równej 1 m, obliczenia będą wyglądały:

V = 1 m³, co odpowiada 1000000 cm³.

W skrócie, aby skutecznie obliczyć objętość sześcianu, najpierw dokładnie zmierz długość krawędzi, a potem zastosuj wzór V = a³, co pozwoli ci szybko uzyskać wynik w odpowiednich jednostkach.

Jak zmierzyć długość krawędzi sześcianu?

Aby zmierzyć długość krawędzi sześcianu, najlepiej skorzystać z linijki lub innego precyzyjnego narzędzia pomiarowego. Pomiar wykonuje się od jednego wierzchołka do drugiego, prowadząc wzdłuż krawędzi. Długość ta, znana również jako długość boku, stanowi kluczowy wymiar! Jest ona niezbędna do dalszych obliczeń, takich jak objętość i pole powierzchni sześcianu.

Wartości długości powinny być podawane w odpowiednich jednostkach, np. centymetrach (cm) lub metrach (m), aby obliczenia były dokładne. Precyzyjne zmierzenie krawędzi jest naprawdę istotne, ponieważ nawet niewielkie błędy w tym pomiarze mogą znacząco wpłynąć na wyniki obliczeń objętości oraz powierzchni.

Jak poprawnie wykonać obliczenie objętości?

Aby obliczyć objętość sześcianu, wystarczy zastosować wzór V = a³, gdzie „a” to długość krawędzi. Oto prosty przewodnik, który poprowadzi Cię przez ten proces:

Zmierz długość krawędzi: Możesz użyć linijki lub innego przyrządu pomiarowego. Pamiętaj, by stosować odpowiednie jednostki – na przykład centymetry (cm) lub metry (m).
Oblicz potęgę trzecią: Weź wartość długości krawędzi i pomnóż ją przez samą siebie trzy razy. Na przykład, jeśli długość krawędzi wynosi 2 cm, obliczenie będzie wyglądać tak: V = 2 cm × 2 cm × 2 cm, co daje 8 cm³.
Jednostki objętości: Upewnij się, że Twój wynik jest wyrażony w odpowiednich jednostkach, jak centymetry sześcienne (cm³) lub metry sześcienne (m³). W przypadku użycia innych jednostek, koniecznie przelicz je, by uzyskać poprawny wynik.

Kiedy zastosujesz te kroki, z łatwością obliczysz objętość sześcianu. Wzór V = a³ upraszcza cały proces obliczeń, co jest niezwykle istotne w matematyce oraz naukach przyrodniczych.

Czym jest a³ i dlaczego jest stosowane?

Wyrażenie a³ oznacza podniesienie długości krawędzi sześcianu „a” do potęgi trzeciej. Można to osiągnąć, mnożąc tę długość przez siebie trzykrotnie. Taki sposób obliczania wynika z definicji objętości sześcianu, która określa przestrzeń zajmowaną przez tę bryłę w trzech wymiarach.

Potęgowanie do trzeciego stopnia odgrywa kluczową rolę przy rozważaniach związanych z sześcianem, ponieważ wskazuje na to, że wszystkie jego wymiary, czyli długości krawędzi, są sobie równe. Dlatego korzystając z wzoru V = a³, można szybko i sprawnie określić objętość sześcianu. Taki sposób obliczeń ma ogromne znaczenie w matematyce, a także w wielu innych dziedzinach, takich jak:

inżynieria,
architektura,
projektowanie przestrzeni.
optymalizacja przestrzeni.
porównywanie objętości różnych sześcianów.

Jednostki objętości używane przy sześcianie

Jednostki objętości odgrywają kluczową rolę w obliczeniach związanych z sześcianem. Istnieją trzy główne jednostki, które warto znać:

metry sześcienne (m³),
decymetry sześcienne (dm³),
centymetry sześcienne (cm³).

Wybór odpowiedniej jednostki zależy od wielkości rozważanego sześcianu. Dla większych obiektów korzystniejsze będą metry sześcienne, podczas gdy centymetry sześcienne idealnie sprawdzą się w odniesieniu do mniejszych elementów.

Weźmy jako przykład sześcian o krawędzi wynoszącej 1 metr – jego objętość wynosi 1 m³. Natomiast sześcian o boku 10 cm ma objętość równą 1 000 cm³. Te ilustracje pokazują, jak ważna jest umiejętność konwertowania jednostek. Zrozumienie tych wartości jest nie tylko istotne w kontekście geometrii, ale również znajduje zastosowanie w takich dziedzinach jak inżynieria, budownictwo czy projektowanie.

Konwersja jednostek objętości opiera się na prostych zasadach:

Aby zamienić decymetry sześcienne na metry sześcienne, wystarczy podzielić przez 1000, ponieważ 1 m³ równa się 1000 dm³,
Natomiast w przypadku centymetrów sześciennych należy podzielić przez 1 000 000, gdyż 1 m³ to 1 000 000 cm³.

Te zasady pozwalają na precyzyjne wyrażanie objętości sześcianu w odpowiednich jednostkach miary.

Jakie są podstawowe jednostki objętości (cm³, m³, dm³)?

Podstawowe jednostki objętości, z którymi możemy się spotkać, to:

centymetry sześcienne (cm³),
decymetry sześcienne (dm³),
metry sześcienne (m³).

Centymetr sześcienny reprezentuje objętość sześcianu o krawędzi wynoszącej 1 cm, co odpowiada 1/1000 litra. Z kolei decymetr sześcienny to objętość sześcianu o krawędzi 1 dm i równa się dokładnie 1 litrowi. Metr sześcienny, w kontekście objętości, to z kolei sześcian o boku 1 m, co daje nam aż 1000 litrów.

Te jednostki znalazły zastosowanie w wielu dziedzinach, takich jak matematyka, fizyka czy inżynieria, umożliwiając precyzyjne pomiary objętości zarówno w życiu codziennym, jak i w różnych zastosowaniach technicznych. Warto pamiętać, że przeliczenia między tymi jednostkami mogą być dość proste. Na przykład:

aby przeliczyć metry sześcienne na decymetry sześcienne, wystarczy pomnożyć przez 1000,
w przypadku przeliczenia centymetrów sześciennych na decymetry sześcienne, proces polega na podzieleniu przez 1000.

Jak przeliczać jednostki objętości?

Przeliczanie objętości to kluczowy element zarówno w matematyce, jak i inżynierii. W przypadku sześcianu najczęściej spotykamy jednostki, takie jak metry sześcienne (m³), decymetry sześcienne (dm³) oraz centymetry sześcienne (cm³). Aby efektywnie dokonywać przeliczeń między tymi jednostkami, warto znać podstawowe przeliczniki.

Oto kilka zasad, które ułatwią konwersje:

Metr sześcienny (m³):
- 1 m³ odpowiada 1000 dm³, aby przeliczyć metry sześcienne na decymetry sześcienne, wystarczy pomnożyć przez 1000,
- na przykład: 2 m³ to 2 × 1000, co daje 2000 dm³.
Decymetr sześcienny (dm³):
- 1 dm³ jest równy 1000 cm³, w przypadku przeliczenia decymetrów sześciennych na centymetry sześcienne również wykorzystujemy mnożnik 1000,
- przykład: 3 dm³ to 3 × 1000, co przekłada się na 3000 cm³.
Centymetr sześcienny (cm³):
- gdy chcemy zamienić centymetry sześcienne na decymetry sześcienne, po prostu dzielimy przez 1000,
- na przykład: 5000 cm³ przeliczymy na dm³ przez 5000 ÷ 1000, co daje 5 dm³.

Zrozumienie tych zasad znacznie upraszcza konwersje jednostek objętości. Ułatwia to wykonywanie obliczeń związanych z różnymi formami geometrycznymi, takimi jak sześcian. Dobra orientacja w przelicznikach jest nie tylko przydatna w nauce, ale również w praktycznych zastosowaniach inżynieryjnych.

Jak przeliczyć pole powierzchni a objętość sześcianu?

Aby zrozumieć, jak obliczać pole powierzchni i objętość sześcianu, warto przyjrzeć się, w jaki sposób te dwa parametry są ze sobą powiązane. Pole powierzchni sześcianu można obliczyć za pomocą prostego wzoru: 6 * a², gdzie „a” reprezentuje długość krawędzi. Dzięki temu równaniu łatwo można zauważyć, jak zmiany długości krawędzi wpływają na całkowite pole powierzchni.

Objętość sześcianu, określana wzorem V = a³, pokazuje, że im dłuższa krawędź, tym większa objętość. Dlatego, znajomość pola powierzchni umożliwia obliczenie długości krawędzi, a następnie wykorzystanie tego wyniku do wyliczenia objętości.

Przykładowo, jeśli całkowite pole powierzchni wynosi 54 cm², to można znaleźć długość krawędzi w następujących krokach:

rozpoczynamy od równania: 6 * a² = 54,
następnie przekształcamy: a² = 9,
a ostatecznie: a = 3 cm.

Kiedy mamy już długość krawędzi, możemy obliczyć objętość:

V = a³ = 3³ = 27 cm³.

Ta wzajemna relacja między polem a objętością sześcianu sprawia, że matematyka związana z geometrią staje się prostsza i bardziej intuicyjna.

Jaki jest wzór na pole powierzchni sześcianu?

Wzór na pole powierzchni sześcianu odgrywa istotną rolę w geometrycznych rozważaniach. Aby go obliczyć, wystarczy zastosować prostą formułę: 6 * a², gdzie „a” reprezentuje długość krawędzi sześcianu. Ten wzór uwzględnia sześć równych ścian, które mają formę kwadratów o boku „a”.

pole jednej z tych ścian wynosi a²,
pole powierzchni bocznej wynosi 4 * a².

Zrozumienie tych relacji jest niezwykle użyteczne w różnych zadaniach geometrycznych, a także w praktycznych dziedzinach, takich jak budownictwo czy projektowanie przestrzennych rozwiązań.

Gdy dobrze pojmiemy związki między polem podstawy, polem bocznym a całkowitym polem powierzchni, ułatwi to przeprowadzanie precyzyjnych analiz przestrzennych.

Czy pole powierzchni ma związek z objętością sześcianu?

Pole powierzchni całkowitej i objętość sześcianu są ze sobą ściśle związane, a ich relacja opiera się na długości krawędzi. Sześcian składa się z sześciu identycznych ścian. Aby obliczyć całkowitą powierzchnię, można użyć prostego wzoru:

P = 6a²,

gdzie P oznacza pole powierzchni, a a to długość krawędzi. Dzięki temu równaniu łatwo można określić długość krawędzi, przekształcając je do formy:

a = √(P/6).

Znajomość długości krawędzi jest kluczowa do obliczenia objętości sześcianu. W tym celu używamy wzoru:

V = a³,

gdzie V symbolizuje objętość. Gdy już mamy obliczone pole powierzchni, wystarczy wyznaczyć długość krawędzi, aby następnie móc obliczyć objętość sześcianu.

To powiązanie między powierzchnią a objętością sześcianu jest niezwykle praktyczne. W geometrii oraz w licznych zastosowaniach w codziennym życiu, te zależności ułatwiają wzajemne określanie wymiarów tej bryły.

Czym różni się objętość sześcianu od objętości prostopadłościanu?

Objętości sześcianu i prostopadłościanu różnią się pod wieloma względami, które warto poznać. Sześcian jest szczególnym przypadkiem prostopadłościanu, w którym wszystkie wymiary – długość, szerokość oraz wysokość – są identyczne. Wystarczy zastosować prosty wzór: V = a³, gdzie a oznacza długość krawędzi, aby obliczyć jego objętość.

Z kolei, w przypadku prostopadłościanu, objętość uzyskuje się poprzez pomnożenie długości, szerokości oraz wysokości. Odpowiedni wzór to V = a * b * c. Tutaj a, b i c mogą przyjmować różne wartości, co sprawia, że obliczenia stają się bardziej złożone i wymagają większej precyzji.

W praktyce:

obliczanie objętości sześcianu jest znacznie szybsze i prostsze,
co czyni ten temat bardziej przystępnym w nauczaniu matematyki,
mniejsza liczba wymiarów ułatwia uczniom zrozumienie tych zagadnień.

Jak obliczyć długość przekątnej sześcianu?

Aby obliczyć długość przekątnej sześcianu, posłużymy się wzorem D = a√3, gdzie „a” oznacza długość krawędzi. Przekątna sześcianu łączy dwa przeciwległe wierzchołki, co sprawia, że jej długość przewyższa długość jakiejkolwiek krawędzi.

Obliczenie tej długości jest proste, wystarczy znać długość krawędzi. Przykładowo, gdy długość krawędzi wynosi 5 cm, używając wzoru, obliczamy D = 5√3, co daje nam około 8,66 cm.

Ten wzór D = a√3 bazuje na twierdzeniu Pitagorasa, które stosuje się w trójwymiarowej przestrzeni. W każdej sześcianie, krawędzie, boki oraz przekątne tworzą prostokątne trójkąty. Znajomość długości przekątnej odgrywa kluczową rolę w geometrii oraz ma praktyczne zastosowania w dziedzinach takich jak inżynieria i architektura.

Gdzie stosuje się wzór na objętość sześcianu?

Wzór na objętość sześcianu, V = a³, znajduje szerokie zastosowanie w wielu dziedzinach życia. Jest szczególnie istotny w edukacji, gdzie stanowi fundament nauki o geometrii przestrzennej. Uczniowie poznają, w jaki sposób obliczać objętość sześcianu, co pozwala im lepiej zrozumieć zasady matematyczne i geometryczne.

W inżynierii i architekturze ten wzór odgrywa kluczową rolę w praktycznych obliczeniach związanych z przestrzenią. Architekci oraz inżynierowie używają go przy projektowaniu budynków, co umożliwia im oszacowanie objętości pomieszczeń oraz materiałów niezbędnych do realizacji projektów. Zastosowanie objętości sześcianu ma także znaczenie w pomiarach oraz wypełnianiu przestrzeni, co jest niezwykle ważne w logistyce i magazynowaniu.

Znajomość wzoru na objętość sześcianu pozwala na szybkie i precyzyjne obliczenia, co jest istotne nie tylko w naukach ścisłych i inżynierii, ale również w codziennym życiu. Na przykład, projektanci mogą skuteczniej planować przestrzeń, co wpływa na efektywność działań inżynieryjnych oraz estetykę projektów architektonicznych. Dzięki temu wzór ten staje się nieocenionym narzędziem w wielu praktycznych sytuacjach.

Rola wzoru na objętość w matematyce i inżynierii

Wzór na objętość sześcianu, czyli V = a³, odgrywa kluczową rolę zarówno w matematyce, jak i inżynierii. Jest to podstawowe narzędzie przy obliczaniu objętości brył, które umożliwia określenie, jaką przestrzeń zajmuje sześcian. Ta wiedza jest niezwykle użyteczna w takich dziedzinach jak geometria czy analiza przestrzenna.

W kontekście inżynieryjnym formuła ta znajduje zastosowanie podczas projektowania różnorodnych konstrukcji oraz modułów przestrzennych. Precyzyjne obliczenie objętości jest niezbędne do oszacowania potrzebnych materiałów oraz kosztów produkcji. Inżynierowie, którzy opanowali wzór V = a³, mogą szybko dokonywać obliczeń objętości różnych struktur, co znacznie podnosi efektywność procesu projektowania.

Na przykład, w branży budowlanej sześciany często pełnią rolę podstawowych elementów. Natomiast w logistyce kluczowe staje się określenie wydolności przestrzeni magazynowej. Generalnie rzecz biorąc, znajomość wzoru na objętość sześcianu wspiera innowacje w wielu dziedzinach, łącząc teoretyczne zasady matematyki z praktycznymi wyzwaniami, które stawia inżynieria.

Znaczenie w architekturze i projektowaniu przestrzennym

W dziedzinie architektury i projektowania przestrzennego wzór na objętość sześcianu ma fundamentalne znaczenie w procesie planowania oraz realizacji projektów. Dzięki temu, architekci mogą dokładnie określić wymiary przestrzeni, co istotnie wpływa na zarówno funkcjonalność, jak i estetykę wnętrz.

Obliczenie objętości sześcianu przy użyciu formuły V = a³ pomaga w oszacowaniu ilości materiałów budowlanych potrzebnych do realizacji konstrukcji. Ta informacja odgrywa kluczową rolę w kontekście efektywności kosztowej projektów. W inżynierii wiedza na temat objętości sześcianu staje się niezastąpiona, zwłaszcza przy projektowaniu różnych struktur, takich jak:

zbiorniki,
prefabrykowane elementy.

Kiedy architekci tworzą wstępne plany uwzględniające wymiary sześcianu, zyskują możliwość lepszego modelowania przestrzeni. Dzięki temu mogą analizować użyteczność i optymalizować estetykę, co prowadzi do powstawania harmonijnych oraz funkcjonalnych budynków. Dobrze przemyślana objętość sprzyja efektywnemu zagospodarowaniu przestrzeni, poprawiając takie aspekty jak:

oświetlenie,
wentylacja.

Warto zatem podkreślić, że wzór na objętość sześcianu stanowi istotne narzędzie w pracy architektów. Znacznie przyczynia się do sukcesu w architekturze oraz podnosi efektywność na etapie projektowania przestrzennego.

Przykłady obliczania objętości sześcianu

Obliczanie objętości sześcianu jest naprawdę łatwe i przyjemne. Wystarczy zastosować prosty wzór V = a³, gdzie „a” oznacza długość krawędzi sześcianu. Przyjrzyjmy się kilku przykładom, aby lepiej zrozumieć to zagadnienie.

Jeśli długość krawędzi wynosi 2 cm, objętość obliczamy w następujący sposób: V = 2³, co daje nam 8 cm³,
Gdy mamy krawędź o długości 5 cm, można obliczyć objętość jako V = 5³, co prowadzi nas do wyniku 125 cm³.

W szkołach nauczyciele często wykorzystują interaktywne ćwiczenia, co znacznie ułatwia uczniom przyswajanie tej tematyki. Przykładowe zadania mogą dotyczyć różnych długości krawędzi, na przykład:

3 cm,
7 cm,
10 cm.

Uczniowie są zobowiązani do podania właściwej objętości. Takie praktyki nie tylko pomagają w nauce wzoru, ale również poszerzają ich zrozumienie pojęcia objętości w kontekście realnych aplikacji.

Cały proces obliczeń objętości sześcianu ukazuje, jak istotne jest zrozumienie wzoru oraz umiejętność wyboru odpowiednich jednostek objętości, takich jak cm³ czy m³. Te umiejętności odgrywają kluczową rolę w matematycznym wykształceniu.

Obliczenia przy różnych długościach krawędzi

Obliczanie objętości sześcianu przy różnych długościach krawędzi odgrywa istotną rolę w matematyce. Umożliwia to zrozumienie związku między długością krawędzi a objętością bryły. Wzór V = a³ ilustruje, że objętość sześcianu pochodzi z podnoszenia długości jego krawędzi do trzeciej potęgi.

Przykładowo:

kiedy krawędź ma długość 2 cm, obliczamy objętość w ten sposób: V = 2³ = 8 cm³,
dzięki długości krawędzi wynoszącej 5 m, obliczenie przedstawia się jako V = 5³ = 125 m³.

Takie elementarne obliczenia są bardzo pomocne dla uczniów, by zrozumieć, jak objętość zmienia się w reakcji na różne wymiary.

Nawet niewielkie zwiększenie długości krawędzi o 1 jednostkę może znacznie wpłynąć na objętość sześcianu. Uwydatnia to znaczenie dokładnych obliczeń. Regularne ćwiczenie takich zadań z różnymi długościami krawędzi nie tylko rozwija umiejętności matematyczne, ale także prowadzi do głębszego zrozumienia cech sześcianu.

Typowe zadania i ćwiczenia szkolne

Typowe zadania i ćwiczenia w szkole często koncentrują się na praktycznym zastosowaniu matematycznych wzorów, szczególnie w geometrii. Weźmy na przykład sześcian. Uczniowie niejednokrotnie obliczają jego objętość, korzystając z wzoru V = a³, gdzie „a” oznacza długość krawędzi. Oto kilka przykładów zadań, które można zrealizować:

obliczanie objętości sześcianu dla różnych wartości „a”, na przykład, dla sześcianu o krawędzi 4 cm uczniowie powinni wyliczyć V = 4³ = 64 cm³,
rozwiązywanie problemów wymagających przekształcania objętości z centymetrów sześciennych na metry sześcienne i odwrotnie,
obliczanie pola powierzchni sześcianu za pomocą wzoru P = 6a², co pozwala lepiej zrozumieć relacje między objętością a polem powierzchni,
wykorzystanie interaktywnych zadań, które angażują uczniów w praktyczne ćwiczenia przy pomocy programów komputerowych lub aplikacji edukacyjnych,
ułatwienie wizualizacji sześcianu i jego właściwości.

Te ćwiczenia nie tylko rozwijają umiejętności obliczeniowe, ale również pomagają w zrozumieniu właściwości geometrycznych, co jest niezbędne w dalszej edukacji matematycznej.

Najczęstsze błędy przy obliczaniu objętości sześcianu

Najbardziej powszechne pomyłki przy obliczaniu objętości sześcianu mają swoje źródło w kilku istotnych kwestiach, które odgrywają kluczową rolę w uzyskaniu prawidłowych wyników.

niewłaściwe mierzenie długości krawędzi,
mylenie potęgowania z mnożeniem,
stosowanie nieodpowiednich jednostek miary,
zaniedbanie konieczności konwersji jednostek objętości,
brak weryfikacji obliczeń.

Dokładność pomiarów ma ogromne znaczenie, ponieważ nawet najmniejsze odstępstwa mogą wpłynąć na ostateczny wynik. Przykładowo, jeśli krawędź będzie zbyt krótka lub zbyt długa, może to prowadzić do znacznych różnic w obliczonej objętości.

Niektórzy uczniowie mają tendencję do błędnego obliczania objętości, mnożąc długość krawędzi, zamiast podnosić ją do potęgi trzeciej. Zgodnie z prawidłowym wzorem V = a³, konieczne jest wyliczenie sześcianu długości krawędzi.

Podczas obliczania objętości sześcianu należy używać spójnych jednostek. Na przykład, jeśli długość krawędzi jest podana w centymetrach, wszystkie obliczenia powinny być wykonane w tej samej jednostce, a wynik objętości będzie w cm³.

Użytkownicy mogą zapominać o niezbędnych przeliczeniach, co prowadzi do pomyłek. Na przykład, przeliczenie litrów na centymetry sześcienne wymaga pomnożenia przez 1000, co czasami umyka ich uwadze.

Aby zminimalizować ryzyko wystąpienia tych błędów, warto przestrzegać ustalonych procedur i regularnie weryfikować swoje obliczenia. Zrozumienie wzoru, precyzja w pomiarach oraz używanie odpowiednich jednostek to istotne elementy, które przyczyniają się do prawidłowego obliczenia objętości sześcianu.