Trójkąt 45 45 90

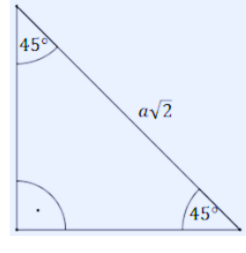
Trójkąt prostokątny 45° 45° 90°

Trójkąt prostokątny 45°-45°-90° to wyjątkowy trójkąt, który tworzy się, gdy dzielimy kwadrat na dwie równe części po przekątnej. Powstają dwa identyczne trójkąty o kątach 45°, 45° i 90°. Każdy z nich jest równoramienny, co oznacza, że oba jego ramiona mają tę samą długość.

W matematyce i geometrii ten typ trójkąta cieszy się dużym zainteresowaniem ze względu na swoje unikalne cechy. Jedną z głównych właściwości jest stosunek długości boków: 1:1:\(\sqrt{2}\). To znaczy, jeśli jedna z przyprostokątnych ma długość \(x\), przeciwprostokątna będzie miała długość \(x\sqrt{2}\). Dzięki tej zależności łatwo można wyliczyć brakujące wymiary w różnych sytuacjach praktycznych.

Ten rodzaj trójkąta pojawia się w wielu obszarach matematyki oraz w edukacji szkolnej. Dzięki swojej symetrii i prostocie ułatwia zrozumienie podstawowych zasad geometrii oraz dobrze ilustruje twierdzenie Pitagorasa.

• funkcje trygonometryczne takie jak sinus,
• cosinus dla kątów 45° wynoszą \(\frac{\sqrt{2}}{2}\),
• co czyni je łatwymi do zapamiętania i użycia podczas obliczeń trygonometrycznych.

Trójkąt prostokątny o kątach 45°-45°-90° nie tylko wspomaga naukę dzięki regularnym proporcjom i kątom, ale również znajduje zastosowanie w zadaniach matematycznych oraz praktycznych przykładach edukacyjnych.

Jak powstaje trójkąt 45° 45° 90°?

Trójkąt 45°-45°-90° powstaje, gdy kwadrat zostaje przecięty wzdłuż swojej przekątnej na dwa identyczne trójkąty prostokątne. Przekątna dzieli kwadrat, tworząc figury o kątach 90°, 45° i 45°. Trójkąty te są równoramienne, co oznacza, że oba przyprostokątne mają taką samą długość. Tego typu konstrukcja jest często wykorzystywana w geometrii do ilustracji rozkładu kątów oraz proporcji boków. Dzięki symetrii i prostocie obliczeń związanych z bokami, ten trójkąt znajduje szerokie zastosowanie w różnych zadaniach matematycznych.

Własności trójkąta 45 45 90

Trójkąt o kątach 45°, 45° i 90° to wyjątkowy rodzaj trójkąta prostokątnego. Wyróżnia się tym, że ma dwa kąty o wartości 45 stopni oraz jeden kąt prosty wynoszący 90 stopni. Charakteryzuje się równością dwóch swoich boków, co sprawia, że jest również trójkątem równoramiennym. Stosunek długości jego boków to 1:1:√2, co oznacza, że przyprostokątne mają identyczną długość, a przeciwprostokątna jest dłuższa o czynnik √2.

W takiej konfiguracji można skorzystać z twierdzenia Pitagorasa. Gdy przyprostokątna wynosi a, wtedy długość przeciwprostokątnej będzie równa a√2. Dzięki symetrii tego trójkąta, obliczenia geometryczne stają się prostsze i bardziej przejrzyste.

Poznanie właściwości trójkąta 45° 45° 90° ułatwia rozwiązywanie wielu problemów matematycznych. Jest on często stosowany w zadaniach z dziedziny trygonometrii czy geometrii analitycznej i odgrywa ważną rolę w nauczaniu tych zagadnień matematycznych.

Kąty w trójkącie 45 45 90

Trójkąt o kątach 45°-45°-90° wyróżnia się wyjątkowym układem kątów. Posiada dwa równe kąty ostre, każdy po 45°, oraz jeden kąt prosty wynoszący 90°. W sumie daje to 180°, co jest zgodne z zasadą dotyczącą sumy kątów w trójkącie. Równość ostrych kątów sprawia, że trójkąt ten jest równoramienny. Taki układ jest charakterystyczny dla trójkątów prostokątnych i pozwala na dalsze badanie jego właściwości, takich jak proporcje boków czy zastosowanie twierdzenia Pitagorasa.

Proporcje boków i ich długości

W trójkącie prostokątnym o kątach 45°, 45° i 90°, proporcje boków odgrywają kluczową rolę. Oba krótsze boki, zwane przyprostokątnymi, są równej długości i możemy je oznaczyć literą „a”. Przeciwprostokątna, natomiast, ma długość „a√2”, co wynika z zastosowania twierdzenia Pitagorasa. Dzięki tym relacjom trójkąt taki jest łatwy do analizy i często znajduje zastosowanie zarówno w zadaniach matematycznych, jak i praktycznych obliczeniach geometrycznych.

Twierdzenie Pitagorasa w trójkącie 45 45 90

Twierdzenie Pitagorasa odgrywa kluczową rolę w geometrii trójkąta o kątach 45°-45°-90°. W takim trójkącie obie przyprostokątne mają równe długości, co czyni go szczególnym przypadkiem trójkąta prostokątnego. Według twierdzenia Pitagorasa, suma kwadratów długości tych przyprostokątnych jest równa kwadratowi przeciwprostokątnej.

Oznacza to, że jeśli długość każdej z przyprostokątnych wynosi a, równanie ma postać: a² + a² = c². Po jego rozwiązaniu otrzymujemy: c = a√2. Ta proporcja boków jest charakterystyczna dla tego typu trójkątów i znacznie ułatwia obliczenia nieznanych wartości w zadaniach matematycznych.

Boki trójkąta 45 45 90

Trójkąt o kątach 45°, 45° i 90° jest wyjątkowym przypadkiem trójkąta prostokątnego. Jego przyprostokątne są zawsze równej długości. Jeśli jedna z nich wynosi a, to druga również ma tę samą wartość. Przeciwprostokątna w takim trójkącie to a√2. Dzięki proporcjom boków 1:1:√2 obliczenia stają się prostsze, gdy znamy długość choćby jednego boku.

W tym typie trójkąta, obie przyprostokątne są sobie równe bez względu na jednostkę miary czy wartość jednej z nich.

Aby określić długość przeciwprostokątnej, wystarczy pomnożyć długość jednej z przyprostokątnych przez pierwiastek z dwóch (√2). Na przykład, jeśli każda przyprostokątna wynosi 5 jednostek, przeciwprostokątna będzie miała 5√2 jednostek.

Przyprostokątne i ich równość

W trójkącie prostokątnym o kątach 45°, 45° i 90°, obie przyprostokątne mają taką samą długość. Jeżeli jedna z nich wynosi a, to druga również będzie miała długość a. Ta równość jest efektem symetrii kątów po 45°. Tym samym, taki trójkąt stanowi szczególny przypadek trójkąta równoramiennego prostokątnego. Stosunek boków w tym typie trójkąta zawsze wynosi 1:1:√2. Wartość √2 odnosi się do długości przeciwprostokątnej, zgodnie z twierdzeniem Pitagorasa. Dzięki stałym proporcjom boków oraz równym przyprostokątnym, trójkąt 45°-45°-90° jest łatwy do analizy i często wykorzystywany w różnorodnych zadaniach matematycznych.

Obliczanie długości przeciwprostokątnej

W trójkącie o kątach 45°, 45° i 90° obliczenie długości przeciwprostokątnej jest łatwe. Wystarczy przemnożyć długość jednej z przyprostokątnych przez pierwiastek kwadratowy z 2. Gdy jedna z przyprostokątnych ma długość „a”, to przeciwprostokątna będzie równa „a√2”. Dzieje się tak, ponieważ w takim trójkącie boki mają stały stosunek: obie przyprostokątne są identyczne, a przeciwprostokątna jest dłuższa o czynnik √2.

Obliczenia związane z trójkątem 45 45 90

Obliczenia związane z trójkątem o kątach 45° 45° 90° są łatwe dzięki jego unikalnym cechom. Pole tego trójkąta można wyznaczyć za pomocą wzoru a²/2, gdzie „a” oznacza długość przyprostokątnej. Na przykład, gdy przyprostokątna mierzy 6 cm, pole wyniesie 18 cm².

Obwód trójkąta to suma dwóch przyprostokątnych oraz przeciwprostokątnej, co możemy zapisać jako: 2a + a√2. Jeśli przyprostokątna ma długość 5 cm, obwód wynosi 5 + 5 + 5√2 ≈ 17,07 cm.

Wysokość w takim trójkącie prostokątnym równoramiennym jest równa długości jednej z jego przyprostokątnych. Zatem dla dowolnej wartości „a”, wysokość również będzie miała tę samą wartość „a”. Dzięki tym formułom możliwe jest szybkie i precyzyjne wykonywanie obliczeń dotyczących tego typu trójkąta.

Jak obliczyć pole trójkąta?

Pole trójkąta prostokątnego o kątach 45°-45°-90° można łatwo obliczyć, korzystając z formuły: P = (a * a) / 2. W tej sytuacji „a” oznacza długość każdej z przyprostokątnych, które w takim trójkącie są sobie równe.

Przykładowo, gdy przyprostokątna mierzy 5 jednostek, pole wynosi:

P = (5 * 5) / 2 = 12,5 jednostek kwadratowych. Ten wzór jest wyjątkowo praktyczny dla tego rodzaju trójkątów ze względu na ich symetryczną budowę i proste stosunki boków.

Jak obliczyć obwód trójkąta?

Aby obliczyć obwód trójkąta prostokątnego o kątach 45°-45°-90°, wystarczy zsumować długości jego boków. W tego typu trójkącie dwa boki są równe i nazywane przyprostokątnymi, oznaczamy je literą „a”. Przeciwprostokątna ma długość równą a√2.

Wzór na obwód wygląda następująco: O = a + a + a√2, co można uprościć do postaci O = 2a + a√2.

Przykładowo, jeśli przyprostokątna mierzy 5 jednostek, to obwód wynosi: O = 2*5 + 5√2 ≈ 19,14 jednostek.

Wysokość trójkąta 45 45 90

W trójkącie prostokątnym o kątach 45°-45°-90°, wysokość równa jest długości jednej z przyprostokątnych. Dzieje się tak, ponieważ dzieli ona przeciwprostokątną na dwie równe części. Co więcej, w takim trójkącie wszystkie przyprostokątne mają identyczną długość, więc wysokość również odpowiada tej samej wartości co przyprostokątna. Dzięki temu obliczenia stają się łatwiejsze i można szybko określić wysokość.

Trygonometria w trójkącie 45 45 90

Trygonometria w trójkącie prostokątnym o kątach 45°-45°-90° odgrywa kluczową rolę w matematycznych obliczeniach. Wartości funkcji trygonometrycznych dla tego trójkąta są stałe i łatwe do zapamiętania:

• sinus kąta 45° to √2/2,
• cosinus kąta 45° to √2/2,
• tangens 45° wynosi 1,
• cotangens 45° również wynosi 1.

Te wartości są niezwykle użyteczne przy ustalaniu długości boków w zadaniach z geometrii. Dzięki funkcjom trygonometrycznym można precyzyjnie określić proporcje między bokami oraz wyznaczyć brakujące długości lub kąty w złożonych zagadnieniach matematycznych. Przykładowo, mając jedną z przyprostokątnych, można bez trudu wyliczyć przeciwprostokątną lub drugą przyprostokątną dzięki niezmiennym wartościom sinusa i cosinusa dla kąta 45°.

Wykorzystanie tych funkcji w takim trójkącie ułatwia rozwiązywanie problemów związanych zarówno z geometrią płaską, jak i analizą przestrzenną. Z uwagi na swoje właściwości ten typ trójkąta często pełni rolę modelowego przykładu podczas nauki matematyki.

Sinus, cosinus, tangens i cotangens

W trójkącie o kątach 45°, 45° i 90°, funkcje trygonometryczne przyjmują unikalne wartości.

• dla kąta 45° zarówno sinus,
• cosinus mają wartość równą √2/2,
• tangens tego kąta jest równy 1,
• iloraz sinusa przez cosinus (√2/2 ÷ √2/2) daje wynik równy jedności,
• cotangens również ma wartość 1, ponieważ jest odwrotnością tangensa.

Te specyficzne wartości są kluczowe w obliczeniach związanych z trójkątami prostokątnymi. Znacznie ułatwiają rozwiązywanie zagadnień geometrycznych i problemów matematycznych dotyczących takich figur. Dodatkowo, te funkcje pozwalają lepiej zrozumieć proporcje boków oraz relacje między nimi w ramach trygonometrii.

Zastosowanie funkcji trygonometrycznych

Funkcje trygonometryczne w trójkącie 45°-45°-90° odgrywają istotną rolę w dokładnych obliczeniach matematycznych. Dzięki symetrii tej figury, sinus oraz cosinus obu kątów wynoszą \(\frac{\sqrt{2}}{2}\), co znacznie upraszcza kalkulacje związane z bokami. Tangens i cotangens dla kąta 45° mają wartość 1, co również ułatwia rachunki.

W praktyce te funkcje pozwalają sprawnie określić długości przeciwprostokątnej i przyprostokątnych, gdy znamy jeden bok. Na przykład, jeśli przyprostokątna ma długość \(x\), to przeciwprostokątna będzie równa \(x\sqrt{2}\).

Dzięki tym właściwościom funkcje trygonometryczne są nieodzowne w naukach ścisłych i inżynierii:

• w inżynierii wykorzystuje się je do projektowania konstrukcji i analizy stabilności,
• w fizyce służą do badania ruchu falowego oraz trajektorii ciał,
• architekci używają ich podczas planowania budowli i zagospodarowania przestrzennego.

Znajomość tych zasad jest niezbędna w edukacji matematycznej. Uczniowie uczą się rozwiązywać zadania geometryczne oraz algebraiczne z zastosowaniem funkcji trygonometrycznych.

Zastosowanie trójkąta 45 45 90 w zadaniach matematycznych

Trójkąt o kątach 45° 45° 90° jest często wykorzystywany w matematyce, zwłaszcza w geometrii oraz trygonometrii. W edukacji pełni rolę w nauce proporcji boków i właściwości kątów. Jego stałe proporcje boków (1:1:√2) upraszczają obliczenia, co jest przydatne na przykład przy wyznaczaniu przekątnych kwadratów.

W praktycznych zastosowaniach trójkąt ten używany jest do mierzenia wysokości budynków czy drzew za pomocą prostych metod trygonometrycznych. W dziedzinie architektury i inżynierii umożliwia szybkie i precyzyjne projektowanie elementów konstrukcyjnych, takich jak dachy lub nachylenia ścian.

Funkcje trygonometryczne tego trójkąta, jak sinus czy cosinus, ułatwiają ustalanie długości boków w przypadku znanego kąta prostego. Na przykład, mając długość jednej z przyprostokątnych, można łatwo obliczyć długość przeciwprostokątnej dzięki relacjom trygonometrycznym.

W nauce matematyki trójkąt ten stanowi narzędzie do rozwiązywania różnorodnych problemów geometrycznych i trygonometrycznych. Dlatego też jest nieodzownym elementem programu nauczania.

Przykładowe zadania i rozwiązania

Rozważmy zadanie: Oblicz długość przeciwprostokątnej w trójkącie o kątach 45°, 45° i 90°, gdy jedna z przyprostokątnych ma długość 5 m. W takim trójkącie, przeciwprostokątna jest równa iloczynowi przyprostokątnej i √2. Stąd wzór: k = a√2, gdzie a to długość przyprostokątnej. Zatem k = 5√2 m.

Innym przykładem może być obliczenie pola tego trójkąta. Pole (P) można znaleźć za pomocą wzoru P = (a²)/2, gdzie a to jedna z przyprostokątnych. Jeśli przyprostokątna ma długość 5 m, pole wynosi P = (5²)/2 = 12,5 m².

Te przykłady pokazują, jak można wykorzystać właściwości geometryczne do rozwiązywania matematycznych problemów związanych z trójkątem o kątach 45°, 45° i 90°.

Praktyczne zastosowania w edukacji matematycznej

Trójkąt 45°-45°-90° odgrywa ważną rolę w matematyce, zwłaszcza w dziedzinach takich jak geometria i trygonometria. Jego symetria oraz proporcje ułatwiają zrozumienie kątów prostych i cech trójkątów równoramiennych. Dzięki niemu uczniowie mogą skutecznie obliczać długości boków kwadratów oraz przekątnych. Przykładowo, podczas pomiaru wysokości budynków, ten rodzaj trójkąta dostarcza precyzyjnych wyników dzięki zastosowaniu funkcji trygonometrycznych takich jak sinus czy cosinus. Jest niezrównany w rozwiązywaniu praktycznych problemów i stanowi fundament wielu zagadnień matematycznych na różnych etapach edukacji.