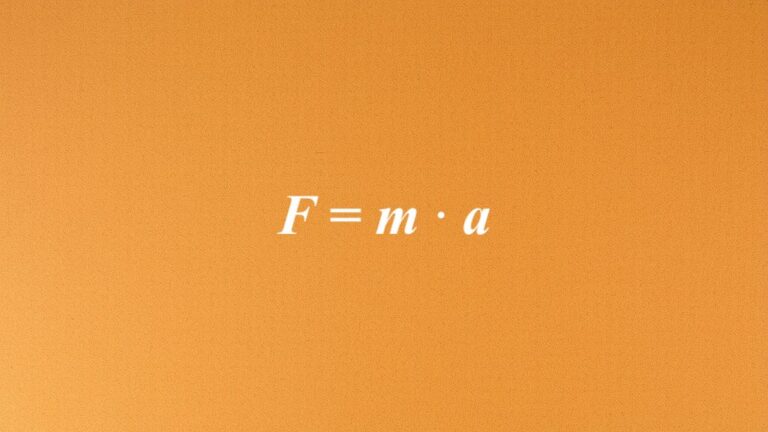Mnożenie macierzy

Mnożenie macierzy to istotna operacja matematyczna, wykorzystywana w wielu dziedzinach, takich jak algebra liniowa, fizyka czy informatyka. Polega ona na połączeniu dwóch macierzy w celu utworzenia nowej. Aby dobrze ją zrozumieć, warto poznać jej definicję i podstawowe zasady.

gdy mnożymy macierz A o wymiarach m×n przez macierz B o wymiarach n×p, wynikiem jest macierz C o wymiarach m×p,
elementy tej nowej macierzy obliczamy jako sumę iloczynów odpowiednich elementów wierszy z A i kolumn z B,
to fundamentalna reguła tej operacji.

W praktyce zastosowanie mnożenia macierzy obejmuje przekształcenia liniowe i rozwiązywanie równań. Trzeba jednak pamiętać o zgodności wymiarów – liczba kolumn pierwszej macierzy musi odpowiadać liczbie wierszy drugiej.

Opanowanie tych podstaw umożliwia zgłębianie bardziej skomplikowanych zagadnień algebry liniowej oraz jej praktycznych zastosowań w nauce i technologii.

Co to jest mnożenie macierzy?

Mnożenie macierzy to ważna operacja matematyczna, która łączy dwie macierze w jedną nową. Przykładowo, gdy mnożymy macierz A o wymiarach m×n przez macierz B o wymiarach n×p, otrzymujemy macierz C o rozmiarach m×p. Każdy element tej nowej macierzy jest wynikiem sumy iloczynów elementów z wierszy pierwszej i kolumn drugiej macierzy. Proces ten odgrywa kluczową rolę w transformacjach liniowych oraz przy rozwiązywaniu układów równań.

Warunki zgodności wymiarów

Aby pomnożyć dwie macierze, trzeba zadbać o zgodność ich wymiarów. Innymi słowy, liczba kolumn w pierwszej macierzy (A) musi odpowiadać liczbie wierszy w drugiej macierzy (B). Na przykład, gdy macierz A ma wymiary m×n, a B n×p, możliwe jest ich pomnożenie. W efekcie otrzymamy macierz C o wymiarach m×p. Zrozumienie tych zasad jest niezbędne do prawidłowego mnożenia macierzy.

Notacja i zapis mnożenia macierzy

W notacji dotyczącej mnożenia macierzy używamy symbolu „×” do oznaczania tej operacji, co zapisujemy jako A × B = C. W tym przypadku A i B to macierze, które poddajemy obliczeniom, a C to wynikowa macierz. Gdy macierz A ma rozmiar m×n, a B rozmiar n×p, ich iloczyn daje nową macierz C o wymiarach m×p. Elementy tej nowej macierzy powstają poprzez sumowanie iloczynów odpowiednich elementów z wiersza pierwszej i kolumny drugiej macierzy. Taki sposób zapisu zapewnia klarowność oraz jednoznaczność w przedstawianiu procesu obliczeniowego i jego rezultatów.

Mnożenie macierzy przez liczbę

Mnożenie macierzy przez liczbę, zwane również mnożeniem przez skalar, polega na przemnożeniu każdego elementu macierzy przez określoną wartość. Mając macierz A i skalar k, wynik zapiszemy jako kA. Istotne jest to, że rozmiary macierzy pozostają niezmienione – nowa macierz zachowuje te same wymiary co pierwotna.

Przykładowo, rozważmy macierz

[[1, 7, 3],
[0, 4, -2]]

oraz skalar o wartości 5. Po pomnożeniu każdego elementu tej macierzy przez 5 otrzymamy

[5 * 1, 5 * 7, 5 * 3], = [5, 35, 15],
[5 * 0, 5 * 4, 5 * -2]] = [0, 20, -10]]

To doskonale ilustruje, jak łatwo można zmienić wszystkie wartości w macierzy poprzez jednolite zwiększenie lub zmniejszenie ich liczbowej wartości.

Ten proces odgrywa istotną rolę w wielu dziedzinach matematyki oraz analizy danych. Pozwala między innymi na skalowanie wektorów czy dostosowanie jednostek miarowych w równaniach liniowych. Dzięki temu operacja ta jest powszechnie wykorzystywana w obliczeniach naukowych i inżynierskich.

Definicja i zasady

Mnożenie macierzy przez skalar polega na przemnożeniu każdego składnika macierzy przez określoną liczbę, co tworzy nową macierz o takich samych rozmiarach. Każdy element tej nowej struktury stanowi wynik iloczynu odpowiedniego elementu oryginalnej macierzy i skalara. Na przykład, gdy mamy macierz A i mnożymy ją przez skalar k, każdy element a_ij w nowej macierzy wynosi a_ij * k. Jest to podstawowa operacja w algebrze liniowej z szerokim zastosowaniem w matematyce i jej różnorodnych dziedzinach.

Przykłady mnożenia przez skalar

Mnożenie macierzy przez skalar polega na przemnożeniu każdego jej elementu przez określoną wartość. Weźmy dla przykładu macierz A = [[1, 2], [3, 4]] oraz skalar k = 2. Proces ten wymaga pomnożenia wszystkich składników macierzy A przez dwójkę. W efekcie otrzymujemy nową macierz:

2A = [[2×1, 2×2],
[2×3, 2×4]],
co daje wynik w postaci [[2, 4], [6, 8]].

To proste działanie ilustruje znaczenie tej operacji w matematyce oraz jej zastosowanie w przekształceniach geometrycznych i skalowaniu danych.

Mnożenie macierzy przez macierz

Mnożenie macierzy przez inną jest fundamentalnym zagadnieniem w algebrze liniowej. Polega na mnożeniu wierszy jednej macierzy przez kolumny drugiej, co pozwala na uzyskanie wartości nowej macierzy. Kluczowe jest, by liczba kolumn pierwszej odpowiadała liczbie wierszy drugiej.

Wynikowe elementy otrzymujemy, sumując iloczyny odpowiednich par elementów z wiersza i kolumny. Na przykład wartość c[i,j] w macierzy C obliczamy, sumując iloczyny wszystkich elementów z odpowiedniego wiersza A i kolumny j z B. Proces ten powtarzamy dla każdej kombinacji wiersza i kolumny, tworząc kompletną nową macierz.

Metoda ta znajduje zastosowanie przy rozwiązywaniu wielu problemów matematycznych oraz naukowych. Od przekształceń liniowych po analizy danych — mnożenie macierzy ma szerokie zastosowanie zarówno teoretyczne, jak i praktyczne, szczególnie w inżynierii i informatyce.

Proces mnożenia wierszy przez kolumny

Mnożenie wierszy przez kolumny stanowi kluczowy etap w procesie mnożenia macierzy. Polega ono na uzyskaniu każdego elementu nowej macierzy poprzez sumowanie iloczynów odpowiadających sobie elementów z wiersza pierwszej macierzy i kolumny drugiej. Aby to było wykonalne, liczba kolumn pierwszej macierzy musi równać się liczbie wierszy drugiej.

Przykładowo, by obliczyć element c[i,j] macierzy C, postępujemy następująco:

wybieramy i-ty wiersz z macierzy A,
wybieramy j-tą kolumnę z B,
mnożymy odpowiednie elementy tych wektorów,
dodajemy wyniki.
Proces ten powtarzamy dla każdej pary wiersz-kolumna, aż uzyskamy wszystkie wartości nowej macierzy.

W praktyce oznacza to, że mając dwie macierze: A o wymiarach m x n oraz B o wymiarach n x p, otrzymana macierz C będzie miała rozmiary m x p. Każdy jej element jest efektem opisanego wyżej procesu dla właściwych par wierszy i kolumn początkowych macierzy.

Iloczyn macierzy i jego wymiary

Iloczyn macierzy A i B prowadzi do powstania nowej macierzy C. Gdy macierz A ma wymiary m×n, a B n×p, to rozmiar C wynosi m×p. Rozmiary tej nowej macierzy wynikają z liczby wierszy w A oraz kolumn w B. Przykładowo, jeśli A składa się z 3 wierszy i 2 kolumn (3×2), a B z 2 wierszy i 4 kolumn (2×4), wtedy otrzymana macierz będzie miała rozmiar 3×4. Warunkiem pomyślnego mnożenia jest jednak zgodność liczby kolumn pierwszej macierzy z liczbą wierszy drugiej.

Przykłady mnożenia macierzy

Mnożenie macierzy można zilustrować, używając przykładowych macierzy A i B. Przyjmijmy, że A = [[1, 2], [3, 4]], a B = [[5, 6], [7, 8]]. Wynikiem tego mnożenia jest nowa macierz C = [[19, 22], [43, 50]]. Elementy macierzy C są wynikiem sumowania iloczynów odpowiednich elementów z wierszy pierwszej macierzy oraz kolumn drugiej.

Dla przykładu pierwszy element C (19) obliczamy jako:

(1×5)
(2×7)
co daje nam łącznie 19.

Takie operacje są fundamentalne w algebrze liniowej i znajdują zastosowanie choćby w przekształceniach liniowych czy rozwiązywaniu układów równań.

Własności mnożenia macierzy

Mnożenie macierzy wyróżnia się kilkoma kluczowymi właściwościami, które mają istotne znaczenie w algebrze liniowej:

nieprzemienność,
łączność,
rozdzielność względem dodawania.

Nieprzemienność oznacza, że dla dowolnych macierzy A i B wynik iloczynu AB może różnić się od BA. Ta charakterystyka jest ważna przy analizie systemów równań i przekształceniach liniowych.

Łączność umożliwia dowolne grupowanie iloczynów bez wpływu na rezultat: (AB)C = A(BC). Dzięki temu można upraszczać wyrażenia i lepiej organizować obliczenia w bardziej złożonych operacjach matematycznych.

Rozdzielność względem dodawania oznacza, że dla dowolnych macierzy A, B i C spełnione są równania: A(B + C) = AB + AC oraz (A + B)C = AC + BC. Rozdzielność ułatwia dzielenie zadań na mniejsze części oraz manipulację wyrażeniami algebraicznymi.

Znajomość tych właściwości jest niezbędna w zaawansowanej matematyce i informatyce, zwłaszcza w takich dziedzinach jak przetwarzanie sygnałów czy analiza danych.

Łączność i rozdzielność

Łączność w mnożeniu macierzy polega na tym, że zmieniając kolejność operacji, nie wpływamy na wynik końcowy. Przykładowo, dla trzech macierzy A, B i C zawsze możemy zapisać: (AB)C = A(BC). Jest to niezwykle użyteczna cecha, gdyż umożliwia swobodne grupowanie działań bez wpływu na ostateczny rezultat.

Z kolei rozdzielność odnosi się do operacji dodawania. Jeśli mamy macierz A oraz sumę B + C, obowiązuje zasada: A(B + C) = AB + AC. Dzięki tej właściwości można rozdzielać mnożenie przez sumę macierzy, co znacznie ułatwia obliczenia i upraszcza wyrażenia algebraiczne.

Obydwie te cechy odgrywają kluczową rolę w analizie algebraicznej i mają szerokie zastosowanie zarówno w matematyce, jak i informatyce.

Nieprzemienność mnożenia macierzy

Nieprzemienność mnożenia macierzy to istotna właściwość, która odróżnia tę operację od zwykłego mnożenia liczb. Oznacza ona, że dla macierzy A i B iloczyn AB nie jest równy BA, co oznacza, że zamiana miejscami tych macierzy zmieni wynik.

Przykładowo:

jeśli A jest macierzą o wymiarach 2×3,
B ma wymiary 3×2,
to produkt AB będzie miało wymiary 2×2.

Z kolei BA przyjmie wymiary 3×3. Ta różnica podkreśla wagę kolejności podczas obliczeń z użyciem mnożenia macierzy.

Warto mieć to na uwadze przy rozwiązywaniu zadań matematycznych oraz w kontekstach inżynieryjnych i naukowych.

Algorytmy mnożenia macierzy

Algorytmy mnożenia macierzy odgrywają istotną rolę zarówno w matematyce, jak i informatyce. Najbardziej podstawowy z nich to algorytm naiwny, który dla macierzy kwadratowych wymaga wykonania O(n^3) operacji. Choć jest łatwy do zrozumienia, przy dużych macierzach staje się niepraktyczny ze względu na wysoką złożoność obliczeniową.

Rok 1969 przyniósł przełom dzięki Volkerowi Strassenowi, który zaprezentował efektywniejszą metodę o złożoności O(n^{2.807}). Jego podejście opiera się na podziale macierzy i redukcji liczby operacji mnożenia w porównaniu do tradycyjnego sposobu. To odkrycie otworzyło drogę do opracowania jeszcze bardziej zaawansowanych algorytmów.

Przykładem może być metoda Coppersmitha-Winograda, która osiąga jeszcze niższą złożoność wynoszącą O(n^{2.376}). Chociaż implementacja tego algorytmu jest skomplikowana, umożliwia znaczne skrócenie czasu przetwarzania dużych zbiorów danych.

Takie algorytmy znajdują zastosowanie w wielu dziedzinach nauki i technologii, gdzie szybkość operacji na obszernych danych jest krytyczna – na przykład:

w grafice komputerowej,
w analizie big data.

Co więcej, nieustanne badania nad optymalizacją obliczeń pozwalają osiągać coraz lepsze rezultaty przy mniejszym zużyciu zasobów.

Podstawowe algorytmy i ich złożoność obliczeniowa

Podstawową metodą mnożenia macierzy jest tradycyjny algorytm, którego złożoność wynosi O(m × n × p). Wartości m, n i p reprezentują wymiary macierzy wejściowych. Polega on na tym, że każdy wiersz jednej macierzy mnoży się przez kolumnę drugiej, co powtarza się dla każdej pary wiersz-kolumna.

Jednakże algorytm Strassena to bardziej zaawansowane rozwiązanie. Redukuje złożoność do O(n^log2(7)), co odpowiada mniej więcej O(n^2.81). Szybsze działanie osiąga dzięki podziałowi dużych macierzy na mniejsze części i rekursywnemu wykonywaniu operacji.

Zrozumienie tych metod jest kluczowe przy pracy z obszernymi zbiorami danych. Są one niezwykle przydatne w takich dziedzinach jak grafika komputerowa czy przetwarzanie naukowych informacji, gdzie wymagane są skomplikowane obliczenia.

Techniki optymalizacji, w tym tiling

Techniki optymalizacji, takie jak tiling, odgrywają istotną rolę w poprawie wydajności mnożenia macierzy. Metoda ta polega na podziale dużych macierzy na mniejsze fragmenty, co umożliwia efektywniejsze wykorzystanie pamięci podręcznej procesora. W rezultacie znacznie maleje liczba operacji związanych z dostępem do pamięci, co jest kluczowe przy obliczeniach. Tiling szczególnie dobrze sprawdza się w przypadku pracy z ogromnymi macierzami, gdzie optymalizacja dostępu do danych potrafi znacząco przyspieszyć działanie algorytmu.

tiling,
równoległe przetwarzanie,
specjalizowane algorytmy opracowane dla konkretnych architektur sprzętowych.

Zastosowania mnożenia macierzy

Mnożenie macierzy odgrywa kluczową rolę w przekształceniach liniowych i rozwiązywaniu układów równań. Macierze umożliwiają reprezentację transformacji przestrzeni, co znacznie ułatwia modelowanie zmian w układach współrzędnych. W grafice komputerowej są one niezbędne do operacji takich jak skalowanie, obracanie czy przesuwanie obiektów w trójwymiarowym środowisku.

W kontekście układów równań liniowych, macierze pozwalają na zapis współczynników i zmiennych w zwięzły sposób. Dzięki temu proces rozwiązywania równań staje się prostszy przy użyciu metod takich jak eliminacja Gaussa czy metoda Cramera, co pozwala na szybkie i precyzyjne uzyskiwanie wyników nawet dla dużych zbiorów danych.

Macierze odgrywają również istotną rolę w sieciach neuronowych, gdzie wspomagają uczenie maszynowe poprzez propagację sygnałów przez różne warstwy sieci. Dlatego właśnie mnożenie macierzy stanowi fundament wielu nowoczesnych algorytmów stosowanych zarówno w informatyce, jak i matematyce stosowanej.

Przekształcenia liniowe i systemy równań

Przekształcenia liniowe to kluczowe zastosowanie mnożenia macierzy, które umożliwiają modelowanie zmian w przestrzeniach wektorowych. Dzięki nim można opisać transformacje, takie jak skalowanie, obrót czy przesunięcie, za pomocą równań liniowych.

W przypadku rozwiązywania systemów równań liniowych, macierze odgrywają istotną rolę w organizacji i manipulacji współczynnikami oraz zmiennymi. Ułatwia to szybkie i skuteczne znalezienie rozwiązań, na przykład poprzez metody takie jak eliminacja Gaussa czy faktoryzacja LU.

Zarówno przekształcenia liniowe, jak i układy równań są ściśle powiązane z teorią macierzową. Z tego względu stanowią one kluczowy element w wielu dziedzinach matematyki stosowanej oraz inżynierii.

Rola w rozkładach macierzy, takich jak LU

Rozkład LU to istotna technika wykorzystująca mnożenie macierzy, która umożliwia rozdzielenie macierzy na dolnotrójkątną (L) oraz górnotrójkątną (U). Dzięki temu metoda ta znacznie ułatwia rozwiązywanie układów równań liniowych. Na przykład, gdy mamy układ Ax = b, najpierw dokonujemy rozkładu LU. Następnie rozwiązujemy równanie Ly = b, co pozwala znaleźć wartości pomocnicze y. Kolejno z równania Ux = y uzyskujemy ostateczne wyniki x.

Dodatkowo, rozkład LU jest niezwykle użyteczny przy obliczaniu wyznaczników macierzy. Wyznacznik można łatwo obliczyć jako iloczyn elementów znajdujących się na diagonali macierzy U. To znacznie upraszcza wszelkie rachunki w algebrze liniowej.