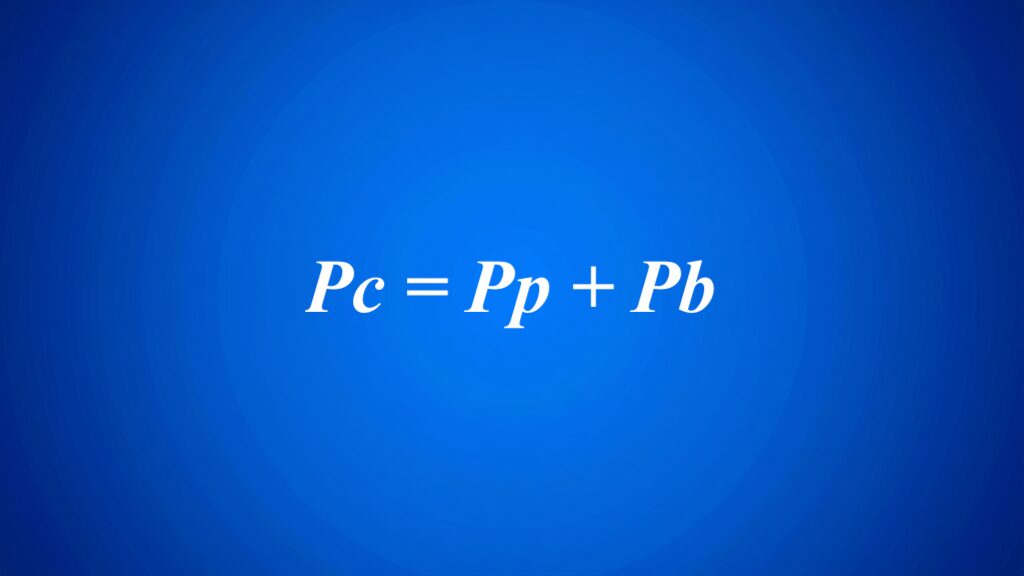Wzór na pole ostrosłupa

Całkowita powierzchnia ostrosłupa to suma pól wszystkich jego ścian, w tym podstawy oraz ścian bocznych. Można to wyrazić wzorem: Pc = Pp + Pb, gdzie Pc oznacza pole całkowite, Pp to powierzchnia podstawy, a Pb reprezentuje pole ścian bocznych.

Wielkość pola podstawy (Pp) jest zależna od jej kształtu — może przybierać formę kwadratu, trójkąta lub innego wielokąta. Natomiast pole powierzchni bocznej (Pb) stanowi sumę pól trójkątów składających się na boki ostrosłupa.

Korzystanie z tego wzoru pozwala precyzyjnie obliczyć całkowitą powierzchnię w różnych zadaniach matematycznych i sytuacjach praktycznych związanych z geometrią przestrzenną.

Co to jest pole powierzchni całkowitej ostrosłupa?

Powierzchnia całkowita ostrosłupa to suma pól wszystkich jego ścian. Składa się z pola podstawy oraz trójkątnych powierzchni bocznych. W matematyce opisuje to wzór: Pc = Pp + Pb, gdzie Pc oznacza pole całkowite, Pp to pole podstawy, a Pb reprezentuje sumę pól ścian bocznych. Obliczanie tej wartości jest kluczowe w geometrii przestrzennej, ponieważ pozwala określić łączną powierzchnię bryły.

Jak obliczyć pole powierzchni całkowitej ostrosłupa?

Aby wyznaczyć całkowite pole powierzchni ostrosłupa, należy podjąć kilka kroków:

określ kształt podstawy i oblicz jej pole (Pp),
jeśli jest to kwadrat lub prostokąt, skorzystaj z odpowiednich wzorów geometrycznych,
przejdź do pola powierzchni bocznej (Pb), które jest sumą pól trójkątnych ścian bocznych bryły,
każda z tych ścian wymaga innego wzoru na pole, zależnie od długości boku podstawy oraz wysokości trójkąta,
ostatecznie, dodaj pole podstawy do pola powierzchni bocznej, aby uzyskać wynik końcowy: Pc = Pp + Pb.

Pole podstawy ostrosłupa

Pole powierzchni podstawy ostrosłupa jest zależne od jej kształtu:

dla kwadratu stosujemy wzór a², gdzie a to długość jego boku,
w przypadku prostokąta używamy formuły a ⋅ b, przy czym a i b oznaczają długości jego boków,
z kolei dla trójkąta równobocznego pole liczymy według wzoru (a² * √3) / 4, gdzie a jest długością boku tego trójkąta.

Kluczowe jest posiadanie dokładnych wymiarów krawędzi podstawy, aby móc zastosować właściwy wzór na obliczenie pola.

Jak obliczyć pole podstawy ostrosłupa?

Aby obliczyć pole podstawy ostrosłupa, najpierw musimy ustalić jej kształt. W przypadku kwadratu korzystamy ze wzoru a², gdzie a to długość boku. Jeżeli mamy do czynienia z prostokątem, używamy formuły a ⋅ b, z a i b jako długościami boków. Dla innych wielokątów należy zastosować odpowiednie metody obliczeniowe. Posiadając dokładne wymiary oraz wiedząc, jaki to rodzaj figury, możemy precyzyjnie wyznaczyć pole podstawy. Pamiętajmy o jednostkach miary i stosujmy je konsekwentnie we wszystkich rachunkach.

Wzory na pole podstawy dla różnych kształtów

Dla różnych kształtów podstawy ostrosłupa stosujemy odpowiednie wzory na pole tej figury.

kiedy mamy do czynienia z kwadratem, gdzie boki są równej długości, pole obliczamy za pomocą wzoru Pp = a²,
w przypadku prostokąta, który ma dwa różne boki, posługujemy się wzorem Pp = a ⋅ b,
natomiast jeśli podstawa to trójkąt, pole liczymy jako Pp = (a ⋅ h) / 2. tutaj „a” oznacza długość podstawy trójkąta, a „h” to wysokość opadająca na tę podstawę.

Każdy z tych wzorów odpowiada specyficznym cechom figury będącej podstawą ostrosłupa.

Pole powierzchni bocznej ostrosłupa

Pole powierzchni bocznej ostrosłupa obliczamy, dodając pola wszystkich jego ścian bocznych. W przypadku ostrosłupa prawidłowego prostego, gdzie każda ze ścian jest identyczna, pole można wyrazić wzorem: Pb = n ⋅ (a ⋅ h) / 2. Tutaj n oznacza liczbę ścian bocznych, a to długość boku podstawy, a h to wysokość ściany.

Jednakże w zależności od kształtu podstawy liczba i wymiary ścian mogą się zmieniać. Dlatego przed przystąpieniem do obliczeń ważne jest dokładne zrozumienie geometrii konkretnego ostrosłupa. Przykładowo, podstawa może być:

kwadratem w ostrosłupie czworokątnym,
trójkątem w wersji trójkątnej.

Pole powierzchni bocznej często pomaga ustalić ilość materiału potrzebnego do pokrycia zewnętrznego ostrosłupa. Dodatkowo znajduje swoje zastosowanie przy projektowaniu konstrukcji architektonicznych opartych na tej formie geometrycznej.

Jak obliczyć pole powierzchni bocznej ostrosłupa?

Aby obliczyć pole powierzchni bocznej ostrosłupa, należy dodać pola wszystkich jego ścian bocznych. W przypadku ostrosłupa prawidłowego prostego, gdzie każda ściana to identyczny trójkąt, można zastosować uproszczony wzór: Pb = n ⋅ (a ⋅ h) / 2. Tutaj n to liczba ścian bocznych, a a i h oznaczają długość boku podstawy oraz wysokość trójkąta.

Jeśli mamy do czynienia z ostrosłupem prawidłowym czworokątnym, każda z czterech ścian jest takim samym trójkątem. Na przykład, przy podstawie o długości 5 cm i wysokości 8 cm, pole jednej ściany wynosi 20 cm². Zsumowanie pól czterech takich trójkątów daje całkowite pole powierzchni bocznej równe 80 cm².

Warto podkreślić, że do wyznaczenia pola niezbędna jest znajomość liczby ścian oraz wymiarów każdej z nich. Ten wzór pozwala szybko obliczyć pole w przypadku regularnych form geometrycznych.

Wzory na pole boczne ostrosłupa

Wzory na obliczanie pola bocznego ostrosłupa zmieniają się w zależności od liczby i kształtu jego ścian. Jeśli podstawą jest prostokąt, pole boczne można wyznaczyć za pomocą wzoru: Pb = a ⋅ h1 + b ⋅ h2. Tutaj „a” i „b” reprezentują długości boków podstawy, natomiast „h1” i „h2” to wysokości odpowiednich trójkątnych ścian. Pole boczne stanowi sumę pól tych trójkątów tworzących powierzchnię ostrosłupa.

Przykłady i ćwiczenia z obliczania pola ostrosłupa

Przykłady oraz ćwiczenia dotyczące obliczania pola ostrosłupa są doskonałym sposobem na utrwalenie wiedzy z matematyki. Zacznijmy od ostrosłupa prawidłowego czworokątnego. Najpierw należy wyznaczyć pole podstawy, które w przypadku kwadratu to \(a^2\). Następnie liczymy pole powierzchni bocznej jako sumę pól wszystkich ścian, z których każda jest trójkątem o podstawie \(a\) i wysokości równej apotemie bocznej.

Przykładowo, rozważmy ostrosłup z kwadratową podstawą, gdzie bok wynosi 4 cm, a wysokość boczna ma 5 cm. Pole podstawy wyniesie wtedy 16 cm². Pole każdej z czterech ścian bocznych to 10 cm², co razem daje 40 cm² dla wszystkich ścian bocznych. Całkowite pole powierzchni stanowi suma pola podstawy i pól ścian bocznych: 56 cm².

W ćwiczeniach praktycznych pojawiają się także zadania z innymi kształtami podstaw jak prostokąty czy trójkąty równoramienne. Kluczowe jest zrozumienie zastosowania wzorów oraz umiejętność dostosowywania się do różnych sytuacji geometrycznych.

Przykład obliczeń dla ostrosłupa prawidłowego czworokątnego

Weźmy pod uwagę ostrosłup prawidłowy czworokątny. Jego podstawa to kwadrat z bokiem o długości 4 cm, a wysokość ścian bocznych wynosi 6 cm. Aby obliczyć całkowitą powierzchnię tego ostrosłupa, zaczynamy od pola podstawy. Pole kwadratu (Pp) wynosi (4 cm)², co daje nam 16 cm².

Kolejny krok to obliczenie powierzchni bocznej. Każda z czterech identycznych ścian bocznych jest trójkątem równoramiennym z podstawą 4 cm i wysokością 6 cm. Pole jednego trójkąta wynosi [(4 cm ⋅ 6 cm) / 2], czyli 12 cm². W związku z tym całkowite pole powierzchni bocznej (Pb) to 4 razy więcej:

Pb = 4 ⋅ 12 cm²
Pb = 48 cm².

Całkowita powierzchnia ostrosłupa to suma pola podstawy i powierzchni bocznej, czyli Pc = Pp + Pb = 16 cm² + 48 cm² = 64 cm². Ten przykład ilustruje krok po kroku sposób obliczeń dla ostrosłupa prawidłowego czworokątnego oraz praktyczne zastosowanie wzorów matematycznych.

Ćwiczenia praktyczne

Ćwiczenie w obliczaniu pola powierzchni ostrosłupa jest kluczowe dla zgłębienia tego tematu. Zacznij od łatwiejszych przykładów, takich jak ostrosłupy z kwadratową podstawą, gdzie znane są długości boków i wysokość ścian bocznych. Następnie spróbuj bardziej skomplikowanych kształtów, na przykład z prostokątnymi lub trójkątnymi podstawami. Istotne jest, aby umieć obliczyć zarówno pole podstawy, jak i powierzchnię boczną. Dzięki temu można lepiej zrozumieć wzór na pole całkowite.

Weźmy na przykład ostrosłup prawidłowy czworokątny o boku podstawy 4 cm i wysokości ściany bocznej wynoszącej 6 cm. Najpierw ustalamy pole podstawy (kwadrat), co daje \(4 \times 4 = 16\) cm². Następnie sumujemy pola trójkątów tworzących ściany boczne. Regularna praktyka z różnorodnymi danymi pozwala lepiej opanować techniki obliczeń oraz przygotowuje do rozwiązywania bardziej zaawansowanych zagadnień matematycznych związanych z geometrią przestrzenną.

Zastosowanie wzoru na pole ostrosłupa w zadaniach matematycznych

Korzystanie ze wzoru na pole ostrosłupa jest bardzo popularne w matematyce, zwłaszcza podczas nauki geometrii. Dzięki niemu można obliczyć całkowitą powierzchnię bryły, co jest niezbędne przy rozwiązywaniu zadań dotyczących różnych kształtów podstawy i wysokości.

typowe zadania obejmują wyznaczanie pola powierzchni dla ostrosłupów z różnymi podstawami, takimi jak kwadrat, prostokąt czy trójkąt,
uczniowie mogą porównywać wyniki dla tych różnych figur oraz analizować wpływ zmian wysokości na całkowitą powierzchnię bryły,
w praktyce wzór ten znajduje zastosowanie również w architekturze i inżynierii,
jest pomocny przy projektowaniu budowli oraz szacowaniu ilości materiałów potrzebnych do stworzenia skomplikowanych struktur przestrzennych,
rozwiązywanie problemów geometrycznych z wykorzystaniem tego wzoru umożliwia głębsze zrozumienie cech przestrzennych brył i rozwija zdolności analityczne.

Jego użyteczność jest szczególnie widoczna tam, gdzie wymagana jest precyzyjna ocena wymiarów i proporcji elementów konstrukcyjnych.

Typowe zadania z wykorzystaniem wzoru na pole ostrosłupa

W matematyce, gdy uczniowie mierzą się z zadaniami dotyczącymi pola ostrosłupa, często muszą obliczać pole całkowite dla różnorodnych kształtów podstaw. Mogą to być na przykład:

kwadraty,
prostokąty,
trójkąty.

Jeśli mamy do czynienia z kwadratową podstawą, dodajemy pole powierzchni bocznej do pola tego kwadratu. W przypadku prostokątnej podstawy uwzględniamy różne długości boków przy dodawaniu pola bocznego. Takie zadania nierzadko wymagają porównywania pól różnych ostrosłupów, co pomaga lepiej zrozumieć, jak kształt i rozmiar podstawy wpływają na pole całkowite. Dodatkowo, praktyczne ćwiczenia wprowadzają wzory w kontekście rozwiązywania rzeczywistych problemów geometrycznych.

Rozwiązywanie problemów z geometrii

Rozwiązywanie problemów związanych z geometrią ostrosłupów wymaga biegłości w stosowaniu różnorodnych wzorów na obliczanie powierzchni. Podstawą jest znajomość wzorów na pole podstawy i pole boczne. Przykładowo, dla ostrosłupa o kwadratowej podstawie, pole podstawy to kwadrat długości jego boku. Pole boczne otrzymujemy, sumując pola wszystkich ścian bocznych, które są trójkątami. Ważne jest również zrozumienie wpływu wysokości ostrosłupa na całkowite pole tej bryły.

Aby efektywnie rozwiązywać zadania matematyczne dotyczące ostrosłupów, uczniowie powinni regularnie ćwiczyć różnorodne problemy geometryczne. Pomocne mogą okazać się praktyczne ćwiczenia oraz przykłady obliczeń dla typowych kształtów podstawy. Dzięki temu można lepiej pojąć zastosowanie teorii w praktyce oraz rozwijać umiejętności analitycznego i logicznego myślenia.

Regularne poznawanie wzorów i metod obliczeniowych umożliwia uczniom skuteczne radzenie sobie z zadaniami dotyczącymi figur geometrycznych takich jak ostrosłupy. To wspiera ich rozwój matematyczny i przygotowuje do bardziej zaawansowanych tematów geometrycznych w przyszłości.