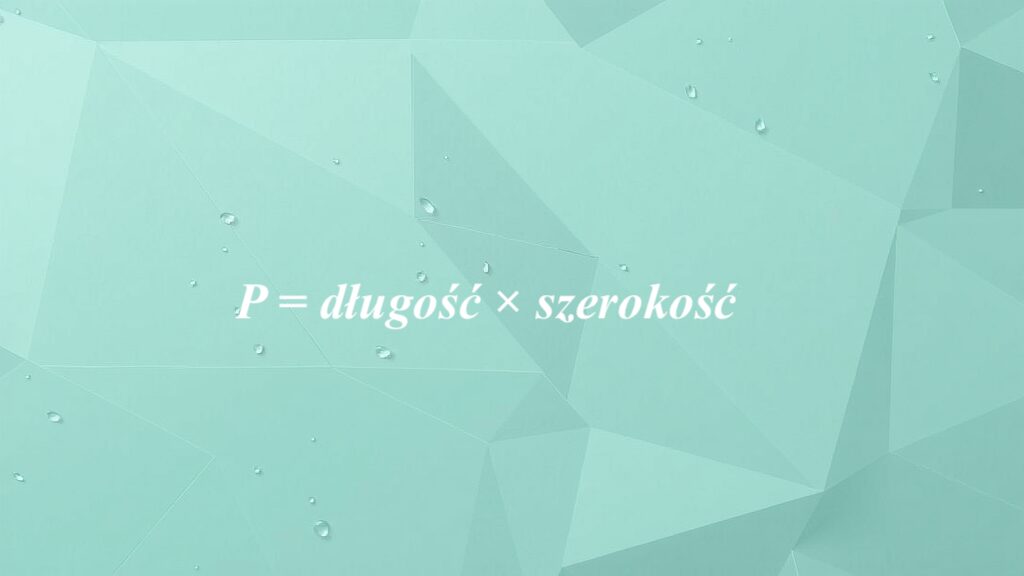Wzór na pole prostokąta
Pole prostokąta można łatwo obliczyć za pomocą wzoru: P = długość × szerokość. Oznacza to, że wystarczy pomnożyć wartości dwóch sąsiadujących boków figury. Zwykle oznaczamy te wymiary jako a i b, gdzie a to długość, a b symbolizuje szerokość. Na przykład dla prostokąta o wymiarach 10 cm na 5 cm pole wynosi 50 cm² (P = 10 cm × 5 cm).
Ten prosty wzór ma wiele praktycznych zastosowań zarówno w życiu codziennym, jak i w nauce. Pozwala szybko oszacować powierzchnię potrzebną do pokrycia określonej przestrzeni czy przy projektowaniu wnętrz. Jest również kluczowy podczas przygotowań do matury z matematyki. Opanowanie podstawowych wzorów geometrycznych jest fundamentem sukcesu każdego ucznia.
Kiedy chcemy użyć przekątnej do wyznaczenia pola prostokąta, warto pamiętać o twierdzeniu Pitagorasa oraz powiązaniu między bokami a przekątną figury. Mimo to, metoda obliczania pola poprzez mnożenie długości i szerokości jest najczęściej stosowana w typowych sytuacjach.
Podstawowy wzór: P = długość · szerokość
Aby obliczyć pole prostokąta, można skorzystać z prostego wzoru: P = długość × szerokość. To podstawowe równanie pozwala określić powierzchnię figury, co jest kluczowe w różnych zadaniach matematycznych. Szybkie mnożenie długości przez szerokość dostarcza nam odpowiedzi.
Na przykład, dla prostokąta o wymiarach 10 cm na 5 cm, pole wyniesie 50 cm² (P = 10 cm × 5 cm). Dzięki temu wzorowi z łatwością ustalisz ilość materiału niezbędną do pokrycia danej powierzchni. Jest to szczególnie przydatne przy takich czynnościach jak:
- układanie płytek,
- malowanie ścian.
Wzór na pole prostokąta z przekątną
Aby wyznaczyć pole prostokąta, znając jego przekątną, możemy skorzystać z twierdzenia Pitagorasa. Przekątna d jest opisana równaniem: d = \(\sqrt{a² + b²}\), gdzie a oraz b to długości boków tego prostokąta. Jeśli mamy informacje o długości przekątnej oraz jednego z boków, możemy łatwo obliczyć drugi bok. Następnie wykorzystujemy wzór na pole: P = a · b, aby uzyskać finalny wynik.
Jak obliczyć pole prostokąta?
Aby wyznaczyć pole prostokąta, wystarczy pomnożyć jego długość przez szerokość. Wzór na pole wygląda następująco: P = długość × szerokość. Na przykład, gdy prostokąt ma wymiary 10 cm na 5 cm, to jego pole wynosi 50 cm².
Jeśli jednak dysponujesz tylko obwodem i jednym z boków, równanie na obwód pomoże znaleźć brakujący wymiar: Obwód = 2 × (długość + szerokość). Pozwala to określić nieznany bok i następnie obliczyć powierzchnię.
Obliczanie pola prostokąta
Aby obliczyć pole prostokąta, musimy znać długości jego boków, oznaczonych jako a oraz b. Metodę tę można wytłumaczyć krok po kroku, co ułatwia jej zrozumienie i zapewnia precyzję.
Na przykład:
- określ długości boków: sprawdź dostępne informacje na temat wymiarów prostokąta,
- jeśli jeden z boków ma 5 metrów, a drugi 3 metry, te liczby będą niezbędne do dalszych obliczeń,
- zastosuj wzór na pole: wykorzystaj podstawową formułę: P = a · b,
- dla naszego przykładu będzie to P = 5 m × 3 m,
- przeprowadź mnożenie: pomnóż długości boków ze sobą,
- otrzymany wynik to P = 15 metrów kwadratowych (m²),
- istotne jest zapisanie wyniku w jednostkach kwadratowych dla zachowania poprawności.
Ćwiczenia praktyczne oraz zadania z rozwiązaniami pozwalają utrwalić tę wiedzę poprzez praktykę różnych przypadków o odmiennych wymiarach i jednostkach miary pola powierzchni. Dodatkowo kalkulatory online stanowią doskonałe narzędzie edukacyjne, umożliwiając szybkie przeliczanie pól prostokątów przy zmianie długości boków czy jednostek miary.
Przykład obliczeń krok po kroku
Aby obliczyć pole prostokąta o wymiarach 15 cm na 25 cm, używamy wzoru P = długość × szerokość. Podstawiając wartości, otrzymujemy: P = 15 cm × 25 cm, co daje nam pole równe 375 cm². Następnie, by znaleźć obwód, stosujemy formułę Obw = 2 × (długość + szerokość). Wprowadzając dane: Obw = 2 × (15 cm + 25 cm) wynosi on 80 cm. Zatem pole wynosi 375 cm², a obwód to 80 cm.
Dla pokoju o wymiarach 5 m na 6 m oraz koszcie położenia posadzki wynoszącym 54 zł za m², najpierw liczymy pole: P = długość × szerokość = 5 m × 6 m = 30 m². Potem mnożymy tę powierzchnię przez cenę za metr kwadratowy: Koszt = P × cena za m² = 30 m² × 54 zł/m². Ostatecznie całkowity koszt będzie równy 1620 zł.
Ćwiczenia interakcyjne i zadania z rozwiązaniami
Ćwiczenia interaktywne i zadania z gotowymi rozwiązaniami odgrywają kluczową rolę w nauce geometrii, szczególnie przy omawianiu pola prostokąta. Umożliwiają one uczniom solidne przygotowanie do matury oraz wszelkich innych egzaminów matematycznych. Dzięki praktycznemu wykorzystaniu wzoru na pole prostokąta, młodzież może nie tylko lepiej zrozumieć materiał, ale również go zapamiętać.
Takie zadania często obejmują różnorodne sytuacje życiowe wymagające zastosowania wzoru P = długość · szerokość lub jego modyfikacji. Rozwiązywanie tych problemów rozwija analityczne myślenie i logiczne rozumowanie, co jest nieocenione podczas egzaminów końcowych.
Interaktywne ćwiczenia dostarczają natychmiastowej informacji zwrotnej, umożliwiając szybkie poprawienie ewentualnych błędów i głębsze zrozumienie tematu. Zadania z rozwiązaniami zawierają szczegółowe przykłady krok po kroku, co bardzo ułatwia samodzielną naukę oraz powtórki przed testami czy egzaminami.
Regularne korzystanie z takich materiałów edukacyjnych jest niezbędne dla efektywnego przyswojenia wiedzy matematycznej i nabrania pewności siebie w obliczaniu pól powierzchni różnych figur geometrycznych.
Praktyczne zastosowania wzoru na pole prostokąta
Wzór na pole prostokąta odgrywa istotną rolę w wielu dziedzinach życia, zarówno zawodowego, jak i osobistego. W architekturze i budownictwie stanowi kluczowy element przy projektowaniu przestrzeni. Architekci posługują się nim do obliczania powierzchni pomieszczeń, co umożliwia precyzyjne określenie ilości potrzebnych materiałów, jak farby czy płytki ceramiczne. Dodatkowo, w projektowaniu wnętrz wzór ten wspiera optymalizację rozmieszczenia mebli oraz innych elementów wyposażenia.
Na co dzień wzór ten okazuje się nieoceniony podczas zakupów związanych z remontem mieszkania. Dzięki niemu można dokładnie określić liczbę paneli podłogowych lub wykładzin koniecznych do pokrycia całego pokoju, minimalizując straty materiału. Podobnie przy nabywaniu tapet lub malowaniu ścian pomaga oszacować niezbędną ilość farby.
- umożliwia precyzyjne określenie ilości potrzebnych materiałów,
- wspiera optymalizację rozmieszczenia mebli oraz innych elementów wyposażenia,
- pomaga dokładnie określić liczbę paneli podłogowych lub wykładzin,
- minimalizuje straty materiału,
- pomaga oszacować niezbędną ilość farby.
Ze względu na swoją prostotę i uniwersalność, wzór ten ma również ogromne znaczenie w edukacji szkolnej. Jego znajomość jest nieodzowna przy rozwiązywaniu zadań matematycznych zarówno na poziomie podstawowym, jak i średniozaawansowanym. Umożliwia rozwijanie zdolności matematycznych uczniów oraz przygotowuje ich do praktycznego wykorzystania wiedzy w dorosłym życiu.
Znajomość zastosowań tego wzoru może zatem znacznie usprawnić codzienne funkcjonowanie oraz efektywne zarządzanie przestrzenią w różnorodnych projektach budowlanych i wnętrzarskich.
W codziennych zadaniach matematycznych
Znajomość wzoru na pole prostokąta okazuje się niezwykle użyteczna w wielu codziennych sytuacjach.
Przykładowo, podczas remontów kluczowe jest obliczanie powierzchni pomieszczeń. Aby określić, ile farby czy tapety potrzebujemy:
- wystarczy zmierzyć długość oraz szerokość ściany,
- zastosować wzór: P = długość · szerokość.
Podobnie przy zakupie materiałów budowlanych, takich jak płytki podłogowe lub panele, znajomość tego wzoru umożliwia dokładne określenie ilości potrzebnego materiału.
- Na przykład pokój o wymiarach 5 na 4 metry ma powierzchnię 20 m²,
- co ułatwia planowanie zarówno kosztów, jak i budżetu.
W życiu codziennym umiejętność obliczania powierzchni wspomaga ocenę efektywności energetycznej budynków oraz projektowanie ogrodów czy tarasów. Takie zdolności pozwalają szybko i skutecznie rozwiązywać wiele praktycznych problemów.
Znaczenie w przygotowaniach do matury
Zrozumienie, jak obliczać pole prostokąta, jest niezwykle ważne podczas przygotowywania się do matury, zwłaszcza w kontekście matematyki i geometrii. Egzamin maturalny często zawiera zadania związane z obliczaniem powierzchni różnych figur geometrycznych. Prostokąt należy do podstawowych kształtów, dlatego uczniowie powinni biegle stosować wzór P = długość × szerokość. Dzięki temu mogą efektywnie rozwiązywać zadania egzaminacyjne. Ta umiejętność okazuje się także przydatna przy bardziej zaawansowanych problemach geometrycznych na maturze.