Wzory na objętość
Obliczanie objętości brył przestrzennych to istotny temat w matematyce i geometrii, umożliwiający precyzyjne określenie, jaką przestrzeń zajmuje dana figura. Dla sześcianu, prostopadłościanu, walca, kuli, stożka oraz ostrosłupa i graniastosłupa istnieją konkretne wzory.
W fizyce objętość określa się jako stosunek masy do gęstości materii. Podobnie w chemii używa się tego pojęcia z oznaczeniem gęstości jako „d”. Zrozumienie tych równań jest niezbędne przy rozwiązywaniu problemów w różnych dziedzinach nauki.
Znajomość wzorów pozwala nie tylko na obliczenia dotyczące objętości różnych brył; pomaga także lepiej pojąć zależności geometryczne i fizyczne rządzące światem materialnym. Ta wiedza jest cenna zarówno w edukacji szkolnej, jak i praktycznych zastosowaniach inżynieryjnych czy architektonicznych.
- sześcian,
- prostopadłościan,
- walec,
- kula,
- stożek,
- ostrosłup,
- graniastosłup.
Dalsze części tekstu szczegółowo omawiają wzory na objętość dla każdej z wymienionych figur geometrycznych.
Wzór na objętość sześcianu
Wzór na objętość sześcianu jest prosty do zapamiętania, co zawdzięczamy jego regularnej strukturze. Sześcian to figura przestrzenna, której każda krawędź ma tę samą długość. Aby znaleźć jego objętość, wystarczy podnieść długość jednej z krawędzi do trzeciej potęgi. Wzór wygląda następująco: V = a³, gdzie „V” oznacza objętość, a „a” długość krawędzi.
Dla przykładu, gdy jedna z krawędzi sześcianu ma 3 cm, obliczamy jego objętość jako 3³ = 27 cm³. Ten wzór jest uniwersalny i można go stosować dla każdego sześcianu, niezależnie od jego wielkości. Sprawdza się zarówno przy dużych przedmiotach, jak i w przypadku niewielkich sześcianów używanych w modelach matematycznych czy fizycznych.
Wzór na objętość prostopadłościanu
Objętość prostopadłościanu obliczamy za pomocą wzoru: V = a * b * h. W tym równaniu:
- a to szerokość,
- b oznacza głębokość,
- h jest wysokością bryły.
Aby znaleźć objętość, wystarczy pomnożyć te trzy wymiary ze sobą. To pozwala nam łatwo określić, jaką przestrzeń zajmuje prostopadłościan. Na przykład, gdy szerokość wynosi 3 m, głębokość to 4 m, a wysokość sięga 5 m, wtedy jego objętość będzie równa 60 m³ (3 * 4 * 5).
Wzór na objętość walca
Aby obliczyć objętość walca, korzystamy ze wzoru V = π * r² * h. Pozwala on określić tę wartość na podstawie pola powierzchni podstawy oraz wysokości bryły. Promień koła (r) jest kluczowy, ponieważ dzięki niemu wyznaczamy pole, które następnie mnożymy przez wysokość (h). W ten sposób otrzymujemy precyzyjny wynik objętości walca, co ma zastosowanie w praktyce i teorii.
Wzór na objętość kuli
Obliczenie objętości kuli jest łatwe dzięki wzorowi:
V = (4/3) * π * r³, gdzie r oznacza promień. Pozwala on precyzyjnie wyznaczyć objętość na podstawie tego parametru.
Przykładowo, jeżeli kula ma średnicę 10 cm, jej promień to 5 cm. Wykorzystując ten wzór:
V = (4/3) * π * 5³, uzyskujemy wynik około 523,6 cm³.
Dzięki temu szybko i bezproblemowo obliczymy objętość dowolnej kuli.
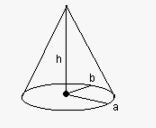
Wzór na objętość stożka
Objętość stożka można wyznaczyć za pomocą wzoru: V = (1/3) * π * r² * h, gdzie r jest promieniem podstawy, a h to wysokość. Dzięki temu równaniu łatwo obliczyć objętość stożka, znając jego wymiary. Jest to niezwykle przydatne w różnych dziedzinach, takich jak inżynieria czy architektura, gdzie dokładne określenie objętości ma istotne znaczenie.
Wzór na objętość ostrosłupa
Wzór na objętość ostrosłupa to V = (1/3) * Pp * h, gdzie Pp oznacza pole podstawy, a h jest wysokością figury. Aby wyznaczyć tę objętość, trzeba znać pole powierzchni podstawy oraz wysokość od wierzchołka do płaszczyzny podstawy. Wzór ten przypomina ten stosowany przy obliczaniu objętości stożka. Pokazuje on, że objętość ostrosłupa o identycznej podstawie i wysokości stanowi jedną trzecią objętości porównywalnego graniastosłupa.
Wzór na objętość graniastosłupa
Aby obliczyć objętość graniastosłupa, posługujemy się wzorem V = Pp * h, co oznacza mnożenie pola podstawy przez wysokość. Pole to zależy od kształtu podstawy, który może być na przykład:
- trójkątny,
- prostokątny.
Wysokość zawsze jest mierzona prostopadle do tej powierzchni. Dzięki tej metodzie możemy dokładnie ustalić objętość dowolnego graniastosłupa, niezależnie od formy jego podstawy.