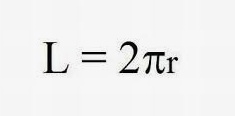Wzór na obwód koła

Wzór na obwód koła

Wzór na obwód koła odgrywa istotną rolę w geometrii i matematyce. Można go przedstawić za pomocą dwóch głównych równań: O = 2 · π · r oraz O = π · d.

• w pierwszym z nich obwód (O) jest uzależniony od promienia (r),
• oznacza to, że wzrost promienia powoduje proporcjonalne zwiększenie się obwodu,
• druga formuła opiera się na średnicy (d),
• średnica jest dwukrotnie większa od promienia,
• jest szczególnie użyteczne, gdy znamy wartość średnicy, upraszczając tym samym nasze obliczenia.

Liczba pi (π), wynosząca około 3,14, to stała matematyczna obecna w obu równaniach. Jest kluczowym elementem wszelkich kalkulacji związanych z kołem. Zrozumienie tych wzorów pozwala na precyzyjne ustalanie długości okręgu w różnych kontekstach praktycznych i teoretycznych.

O = 2 · π · r

Wzór O = 2 · π · r umożliwia wyliczenie obwodu okręgu, gdy znamy jego promień. Promień (r) to odległość między środkiem a brzegiem okręgu. Aby obliczyć obwód, wystarczy pomnożyć tę wartość przez 2 oraz przez liczbę π, która wynosi około 3.14159. Dzięki temu wzorowi łatwo można określić długość linii otaczającej okrąg. Jest on niezwykle ważny w wielu dziedzinach, takich jak inżynieria czy architektura, gdzie dokładność pomiarów jest kluczowa.

O = π · d

Wzór O = π × d umożliwia obliczenie obwodu koła, kiedy znamy jego średnicę. Średnica, oznaczana jako d, to dwukrotność promienia i stanowi linię przechodzącą przez środek okręgu, łączącą dwa przeciwległe punkty na jego obrzeżu. Aby uzyskać obwód (O), wystarczy pomnożyć średnicę przez liczbę pi (\( π \)), której wartość to około 3,14159. Dzięki temu prostemu wzorowi można szybko wyznaczyć całkowitą długość krawędzi okręgu. Jest to niezwykle ważne w wielu dziedzinach matematyki oraz inżynierii.

Zależność między obwodem a promieniem

Zależność między obwodem a promieniem koła jest istotnym elementem geometrii, który można wyrazić za pomocą prostego wzoru: O = 2 · π · r. Wzór ten pokazuje, że obwód (O) rośnie proporcjonalnie do długości promienia (r). Oznacza to, iż zwiększenie promienia powoduje taki sam wzrost obwodu.

Liczba pi (π), wynosząca około 3.14159, jest stałą matematyczną wykorzystywaną do przeliczania promienia na obwód. Dla przykładu, jeśli promień koła wynosi 5 cm, to jego obwód można wyliczyć w następujący sposób:

O = 2 · π · 5 cm ≈ 31.42 cm.

Zrozumienie tej relacji jest istotne zarówno w kontekście rozwiązywania problemów geometrycznych, jak i praktycznych zastosowań codziennych. Wiedza ta przydaje się przy projektowaniu kół czy analizie ruchu okrężnego.

Zależność obwodu od średnicy

W geometrii koła kluczowa jest relacja między obwodem a średnicą. Wzór \( O = π · d \) podkreśla ich proporcjonalność, co oznacza, że podwojenie średnicy prowadzi do dwukrotnego zwiększenia obwodu. Liczba pi (π), wynosząca około 3,14159, pełni rolę stałej matematycznej, która wiąże te dwa parametry. Dzięki tej relacji możemy łatwo obliczyć obwód znając jedynie średnicę, co jest niezwykle przydatne w różnych zastosowaniach geometrycznych i inżynieryjnych.

Jak obliczać obwód okręgu

Aby obliczyć obwód okręgu, mamy do dyspozycji dwa proste wzory, które wybieramy w zależności od dostępnych informacji.

• gdy znamy średnicę, wystarczy pomnożyć ją przez π (około 3,14159), co przedstawia się jako: O = π · d,
• na przykład dla średnicy wynoszącej 10 cm wynik to około 31,4159 cm.
• jeżeli posiadamy wartość promienia, należy go podwoić i pomnożyć przez π,
• wówczas korzystamy ze wzoru: O = 2 · π · r,
• dla przykładu przy promieniu równym 5 cm otrzymujemy obwód około 31,4159 cm.

Obydwa wzory są połączone prostą relacją między promieniem a średnicą: d = 2r. Pozwala to łatwo przechodzić między metodami obliczeń w zależności od tego, jakie dane posiadamy.

Stosowanie tych formuł wymaga jedynie podstawowej znajomości geometrii oraz arytmetyki, a także dostępu do wartości liczby π w dokładności odpowiedniej do konkretnego zadania.

Jak obliczyć obwód ze średnicy: przykład

Aby znaleźć obwód koła, gdy znamy jego średnicę, stosujemy wzór O = π · d. Liczba pi (π) to stała matematyczna o wartości około 3,14159. Przykładowo, dla koła o średnicy 10 cm, mnożymy tę wartość przez π i uzyskujemy O ≈ 31,4159 cm. To proste działanie umożliwia szybkie określenie obwodu koła. Taka metoda okazuje się niezwykle przydatna w wielu dziedzinach nauki i techniki.

Jak znaleźć promień na podstawie obwodu?

Aby wyznaczyć promień na podstawie obwodu okręgu, wystarczy:

• podzielić obwód przez liczbę pi (π ≈ 3,14),
• uzyskać średnicę,
• podzielić średnicę na pół, aby otrzymać promień.

Przykład:

• dla obwodu wynoszącego 44 cm,
• po podzieleniu przez π uzyskujemy około 14 cm jako średnicę,
• dzieląc tę wartość przez 2, otrzymujemy promień równy mniej więcej 7 cm.

Taki sposób obliczeń okazuje się niezwykle przydatny w różnych dziedzinach matematyki i praktycznym zastosowaniu.

Przykłady obliczeń obwodu

Przykłady obliczania obwodu koła pozwalają lepiej zrozumieć, jak w praktyce stosować wzory matematyczne. Przyjrzyjmy się dwóm metodom: wykorzystaniu promienia oraz średnicy.

• kiedy mamy wartość promienia, używamy wzoru \( O = 2 · π · r \),
• przykładowo, jeśli promień wynosi 14 cm, to obwód będzie: \[ O = 2 · π · 14 = 87,9646 \text{ cm} \],
• gdy dysponujemy średnicą, stosujemy formułę \( O = π · d \),
• dla średnicy o długości 28 cm (ponieważ jest to dwa razy większa wartość niż promień), wynik również wynosi: \[ O = π · 28 = 87,9646 \text{ cm} \].

Te przykłady ilustrują zastosowanie liczby pi (π) oraz pokazują relację pomiędzy promieniem a średnicą przy wyznaczaniu obwodu koła.

Jednostki miary obwodu

Jednostki miary obwodu występują zarówno w systemie metrycznym, jak i imperialnym:

• w systemie metrycznym najczęściej spotykamy milimetry (mm), centymetry (cm), metry (m),
• na przykład 1000 mm to 100 cm, co dalej równa się 1 m,
• w systemie imperialnym używa się cali (in), stóp (ft), jardów (yd).

Przykładowo, 12 cali odpowiada jednej stopie, a trzy stopy składają się na jeden jard. Wybór jednostki pomiaru zależy od kontekstu i precyzji, jakiej wymaga dana sytuacja.

Jednostki obwodu i ich konwersja

Zmiana jednostek obwodu jest kluczowa przy pracy z różnorodnymi systemami miar. W metrycznym używamy centymetrów oraz metrów, podczas gdy imperialny opiera się na calach i stopach. Aby skutecznie przeliczać jednostki między tymi dwoma systemami, warto mieć w głowie kilka podstawowych wartości:

• 1 cal odpowiada 2,54 cm,
• stopa to 30,48 cm,
• 1 metr to około 3,281 stopy.

Dzięki temu możemy łatwo zamienić obwód podany w calach lub stopach na centymetry poprzez odpowiednie mnożenie. Taka umiejętność znacząco ułatwia życie inżynierom i projektantom pracującym z danymi pochodzącymi z różnych krajów.

Równie prosta jest odwrotna konwersja – dzieląc długość w centymetrach przez stosowny współczynnik (np. 2,54 dla zamiany na cale), otrzymujemy wynik w mierze imperialnej.

Znajomość tych zależności umożliwia nie tylko poprawne przeliczanie obwodów kół czy innych figur geometrycznych między różnymi miarami. Jest także niezastąpiona przy unikaniu błędów w kalkulacjach związanych z projektowaniem lub produkcją elementów wymagających dokładnych wymiarów.

Jak korzystać z kalkulatora obwodu

Korzystanie z kalkulatora obwodu to proces prosty i intuicyjny. Wystarczy, że wprowadzisz promień lub średnicę okręgu w odpowiednie miejsce. Urządzenie automatycznie obliczy te wartości, prezentując dokładne wyniki dla obwodu oraz pola figury. Możesz również zmieniać jednostki miary zgodnie z własnymi potrzebami, co czyni narzędzie niezwykle wszechstronnym w różnych sytuacjach. Dzięki temu błyskawicznie uzyskasz rezultaty bez konieczności samodzielnego wykonywania obliczeń. Na przykład, gdy wpiszesz średnicę 10 cm, natychmiast otrzymasz informacje:

• obwód wynosi 31,4159 cm,
• pole to 78,5398 cm².