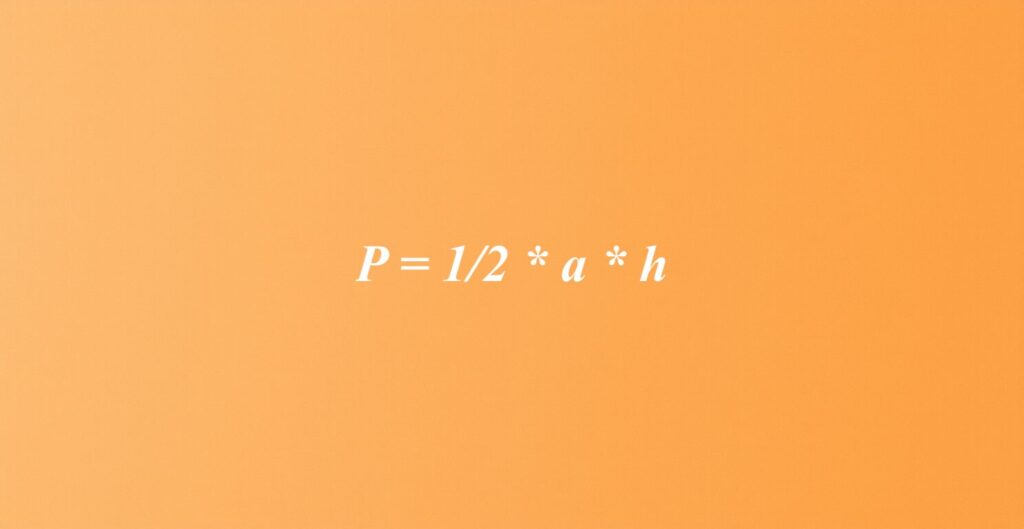Wzór na wysokość trójkąta

Wysokość trójkąta to najkrótsza linia łącząca wierzchołek z przeciwległym bokiem, który określamy mianem podstawy. Ta linia zawsze tworzy kąt prosty z podstawą, co sprawia, że jest prostopadła. Każdy trójkąt dysponuje trzema wysokościami – po jednej z każdego z jego wierzchołków. Te wysokości odgrywają istotną rolę w geometrii, ponieważ są niezbędne do obliczania pola i rozwiązywania różnorodnych problemów związanych z figurami geometrycznymi. Dlatego wysokość trójkąta stanowi kluczowy element w jego analizie i badaniu właściwości.

Jak oznaczamy wysokość w trójkącie?

W trójkącie wysokość zazwyczaj oznaczamy literą h, co stało się standardem w matematyce. Aby precyzyjnie zaznaczyć, do której podstawy jest ta wysokość, dodajemy odpowiedni indeks. Na przykład, h_a to wysokość opuszczona na bok a. Takie oznaczenia upraszczają zapisywanie wzorów oraz rozwiązywanie problemów związanych z trójkątami.

dzięki tym symbolom z łatwością możemy zidentyfikować, która wysokość jest brana pod uwagę,
ułatwiają one zrozumienie, do jakiego boku odnosi się nasze obliczenie,
to znacząco przyspiesza naszą pracę,
zwiększa efektywność obliczeń,
ułatwia naukę i zapamiętywanie wzorów.

Jakie są cechy wysokości w trójkącie?

Wysokość trójkąta to linia prostopadła do podstawy, która łączy wierzchołek z bokiem przeciwnym. Każdy trójkąt dysponuje trzema wysokościami, które zbiegają się w jednym punkcie, określanym jako ortocentrum. Miejsce, w którym wysokość przecina bok, to spodek wysokości.

W przypadku trójkątów równoramiennych oraz równobocznych wysokość dzieli podstawę na dwie identyczne części. Wysokości różnią się jednak w zależności od rodzaju trójkąta. Na przykład:

w trójkącie prostokątnym jedna z wysokości pokrywa się z jedną z przyprostokątnych,
w ostrokątnym trójkącie wszystkie wysokości zbiegają się wewnątrz figury,
w trójkącie rozwartokątnym ortocentrum znajduje się na zewnątrz.

Te różnice w wysokościach wpływają na właściwości geometryczne i obliczenia związane z trójkątami.

Jakie są wzory na wysokość trójkąta?

Wzór z pola trójkąta: h = (2P)/a

Wzór h = (2P)/a umożliwia obliczenie wysokości trójkąta, gdy dysponujemy informacjami o jego polu (P) oraz długości podstawy (a). To jest przekształcenie znanego równania na pole trójkąta, które brzmi P = 1/2 * a * h. Co ważne, to uniwersalne równanie sprawdza się w przypadku każdego trójkąta, niezależnie od jego kształtu.

Aby szybko znaleźć wysokość, wystarczy podstawić wartości pola oraz długości podstawy. Na przykład:

jeśli najpierw obliczymy pole trójkąta korzystając z wzoru Herona,
później możemy użyć wzoru na wysokość, by precyzyjnie określić wartość h.

Zastosowanie tego równania jest niezwykle istotne w sytuacjach, gdy posiadamy długość jednego boku oraz pole figury. Dzięki temu narzędziu obliczanie wysokości trójkąta staje się prostsze i bardziej efektywne.

Wzór trygonometryczny: h = b · sin(α)

Wzór trygonometryczny h = b · sin(α) służy do obliczenia wysokości trójkąta. Dysponując długością jednego z boków, oznaczonego jako b, oraz kątem α, możemy z łatwością określić wysokość, która leży pomiędzy tym bokiem a podstawą.

Funkcja sinus jest tutaj niezbędna, ponieważ pozwala nam na precyzyjne wyliczenie wysokości bez konieczności jej bezpośredniego mierzenia. Tego rodzaju podejście okazało się niezwykle cenne w zadaniach matematycznych, w których posiadamy informacje o kątach oraz długościach boków trójkąta.

Dzięki zastosowaniu wzoru h = b · sin(α) możemy szybko i sprawnie ustalić wysokość, co znacznie przyspiesza obliczenia pola i innych właściwości trójkąta. To wyrażenie znalazło szerokie zastosowanie w trygonometrii, szczególnie podczas analizy kształtów i wymiarów różnych trójkątów.

Obliczanie wysokości przy użyciu wzoru Herona

Wzór Herona to doskonałe narzędzie do obliczania wysokości trójkąta, gdy znamy długości jego trzech boków. Cały proces rozpoczynamy od wyznaczenia pola powierzchni trójkąta. Służy do tego równanie: P = √[p(p − a)(p − b)(p − c)], gdzie p oznacza połowę obwodu, obliczaną jako p = (a + b + c)/2.

Po ustaleniu wartości P, możemy przejść do obliczenia wysokości h względem boku a. W tym celu wykorzystujemy formułę: h = (2P)/a. Ta metoda jest szczególnie użyteczna w sytuacjach, gdy brakuje nam danych o wysokości czy miarach kątów, a jedynie dysponujemy długościami boków. Dzięki temu jesteśmy w stanie dokładnie określić wysokość, bazując wyłącznie na pomiarach boków naszego trójkąta.

Wykorzystanie twierdzenia Pitagorasa do obliczania wysokości

Twierdzenie Pitagorasa jest niezwykle pomocne w obliczeniach wysokości trójkątów prostokątnych i równoramiennych. W przypadku trójkąta prostokątnego wysokość h do przeciwprostokątnej można ustalić według wzoru:

h = \(\frac{(a * b)}{c}\),

gdzie a i b reprezentują przyprostokątne, a c to długość przeciwprostokątnej.

Z drugiej strony, aby wyznaczyć wysokość h w trójkącie równoramiennym, używamy innego wzoru:

h = \(\sqrt{(b² – (\frac{a}{2})²)}\),

tutaj b oznacza długość ramienia, natomiast a to długość podstawy.

Ta metoda umożliwia dokładne obliczenie wysokości, nawet gdy nie możemy jej zmierzyć bezpośrednio. Kiedy prowadzi się wysokość z wierzchołka kąta rozwartym, tworzy się trójkąt prostokątny, co otwiera możliwość zastosowania twierdzenia Pitagorasa do obliczenia poszukiwanej wysokości. Przykładowo, wysokość odgrywa kluczową rolę w obliczaniu pola różnych figur.

Wykorzystanie tego wzoru, opartego na twierdzeniu Pitagorasa, jest efektywne i precyzyjne. Doskonale sprawdza się przy obliczaniu wysokości zarówno w trójkątach prostokątnych, jak i równoramiennych.

Jak obliczyć wysokość w różnych rodzajach trójkątów?

W trójkącie równobocznym wysokość można obliczyć, korzystając z równania: h = (a * √3) / 2, gdzie „a” to długość każdego boku.

W trójkącie równoramiennym wysokość oblicza się przy użyciu wzoru: h = √(b² – (a/2)², gdzie „b” oznacza długość ramienia, a „a” to długość podstawy.

W trójkącie prostokątnym wysokość opadająca na przeciwprostokątną jest określona równaniem: h = (a * b) / c, gdzie „a” i „b” to długości przyprostokątnych, a „c” to długość przeciwprostokątnej.

W trójkątach ostrokątnych i rozwartokątnych ortocentrum, punkt, w którym przecinają się wysokości, może się znajdować zarówno wewnątrz, jak i na zewnątrz figury. Taki układ wpływa na proces obliczania wysokości.

W każdym przypadku wybór odpowiedniego wzoru oraz metoda obliczeń zależą od rodzaju trójkąta i informacji zawartych w zadaniu.

Wysokość w trójkącie równobocznym

W trójkącie równobocznym wysokość można wyliczyć za pomocą prostego wzoru: h = (a · √3) / 2. W tym przypadku „a” oznacza długość boku trójkąta. Ta wysokość:

dzieli podstawę na dwa równe fragmenty,
pełni funkcje dwusiecznej kąta,
pełni funkcje środkowej,
pełni funkcje symetralnej.

Co ciekawe, we wszystkich trójkątach równobocznych wysokości mają taką samą długość. Miejsce, w którym się one spotykają, nosi nazwę ortocentrum. Fascynujące jest to, że ortocentrum zbiegają się z innymi istotnymi punktami trójkąta, co stanowi unikalną cechę tego typu figur geometrycznych.

Dzięki prostocie wzorów, możemy szybko obliczyć wartość wysokości, znając długość boku, co czyni cały proces niezwykle wydajnym.

Wysokość w trójkącie równoramiennym

W trójkącie równoramiennym wysokość opada prosto na podstawę, dzieląc ją na równą pół. Aby obliczyć tę wysokość, możemy skorzystać z następującego wzoru:

h = √(b² – (a/2)²)

W tym równaniu b oznacza długość ramienia trójkąta, a a to długość podstawy. Wykorzystujemy tutaj twierdzenie Pitagorasa, gdyż wysokość, połowa podstawy oraz ramię tworzą trójkąt prostokątny.

Interesującym aspektem trójkątów równoramiennych jest to, że:

wysokości prowadzone do ramion mają tę samą długość,
to jest ich wyróżniająca cecha,
dzięki wzorowi na wysokość możemy dokładnie ustalić jej długość.

Pod warunkiem, że mamy informacje na temat długości boków trójkąta.

Wysokość w trójkącie prostokątnym

W trójkącie prostokątnym, dwa boki, które tworzą kąt prosty, pełnią jednocześnie rolę wysokości. W praktyce oznacza to, że te wysokości pokrywają się z przyprostokątnymi. Aby obliczyć wysokość opadającą na przeciwprostokątną, możemy skorzystać z prostego wzoru: h = (a · b) / c. W tej formule a oraz b oznaczają długości przyprostokątnych, natomiast c to długość przeciwprostokątnej.

Co ciekawe, ortocentrum w trójkącie prostokątnym znajduje się w wierzchołku kąta prostego. Dzieje się tak dlatego, że wspomniane wysokości pokrywają się z przyprostokątnymi. Wzór dotyczący wysokości trójkąta prostokątnego jest niezwykle pomocny, gdyż umożliwia szybkie obliczenie długości wysokości w odniesieniu do przeciwprostokątnej. To narzędzie ma swoje zastosowanie w rozwiązywaniu różnorodnych zadań z zakresu geometrii i trygonometrii.

Co to jest spodek wysokości?

Spodek wysokości to punkt, w którym wysokość trójkąta łączy się z jego podstawą lub jej przedłużeniem. W geometrii trójkąta jest to kluczowy element, ponieważ w tym miejscu wysokość pozwala na precyzyjne określenie odległości oraz umożliwia konstrukcję ortocentrum.

Zrozumienie spodu wysokości jest również istotne w kontekście rozwiązywania problemów związanych z wysokościami trójkąta i analizowaniem jego właściwości. Posiadanie wiedzy na ten temat znacznie ułatwia radzenie sobie z różnorodnymi zagadnieniami geometrycznymi, a także pozwala na odkrywanie bardziej złożonych kwestii związanych z trójkątami.

W jaki sposób wysokości przecinają się w trójkącie?

Wysokości trójkąta, a także ich przedłużenia, łączą się w jednym punkcie, który nazywamy ortocentrum. Jego lokalizacja różni się w zależności od typu trójkąta.

W przypadku trójkąta ostrokątnego ortocentrum znajduje się wewnątrz figury. W trójkącie prostokątnym ten szczególny punkt pokrywa się z wierzchołkiem kąta prostego. Natomiast w trójkącie rozwartokątnym ortocentrum ulokowane jest na zewnątrz trójkąta.

Ortocentrum odgrywa istotną rolę jako punkt charakterystyczny w geometrii, ukazując różnorodność właściwości trójkątów.

Jak długości boków i kąty wpływają na wysokości trójkąta?

Długości boków i kąty w trójkącie mają znaczący wpływ na jego wysokość. Wzór trygonometryczny h = b · sin(α) wskazuje, że wysokość (h) jest uzależniona od długości boku (b) oraz wartości sinusa kąta (α) utworzonego z tym bokiem i podstawą. Zauważ, że im większy jest kąt, tym wyższy stanie się trójkąt przy tej samej długości boku.

Dodatkowo, formuły dotyczące pola trójkąta, takie jak h = (2P)/a, ukazują, w jaki sposób wysokość wyrasta z długości podstawy (a) oraz powierzchni (P). W przypadku trójkątów:

równobocznych,
równoramiennych,
gdzie boki są tej samej długości,
wysokości pozostają identyczne
i są ułożone symetrycznie.

To zjawisko wynika z jednolitości kątów i boków.

Każda zmiana długości boku lub kąta przekłada się na wartość wysokości. Dlatego tak ważne jest, aby znać długości boków oraz miary kątów, co pozwala na precyzyjne obliczenia wysokości trójkąta przy użyciu wzorów trygonometrycznych i geometrycznych.

Jak obliczać wysokość trójkąta w zadaniach matematycznych?

W matematyce, obliczanie wysokości trójkąta opiera się na kilku kluczowych wzorach, które dobieramy w zależności od posiadanych danych. Najbardziej popularny to ten związany z polem trójkąta:

h = (2P)/a,

gdzie P oznacza pole, a a to długość podstawy. Gdy mamy informacje o długościach boków oraz kątach, sięgamy po trygonometrię, korzystając z wzoru:

h = b · sin(α),

z b jako długością boku, oraz α jako kątem przyległym do podstawy. W sytuacji, gdy nie dysponujemy polem, możemy wykorzystać wzór Herona. Najpierw obliczamy pole, korzystając z długości wszystkich boków, a następnie wyznaczamy wysokość.

w trójkątach prostokątnych i równoramiennych często korzystamy z twierdzenia Pitagorasa,
co znacząco upraszcza nasze obliczenia.
Zrozumienie tych wzorów i metod znacząco wspiera efektywność w obliczaniu wysokości w geometrii.

Na czym polegają środkowe w trójkącie i czym różnią się od wysokości?

Środkowa trójkąta to segment, który łączy wierzchołek z punktem położonym na przeciwległym boku – jego środkiem. Co istotne, wszystkie środkowe krzyżują się w punkcie określanym jako środek ciężkości, który dzieli każdą z tych linii w proporcji 2:1 od wierzchołka.

Natomiast wysokości trójkąta mają nieco inne właściwości. Są to odcinki, które zawsze zachowują prostokątne połączenie z podstawą, łącząc wierzchołek z tą dolną linią. W przeciwieństwie do środkowych, które łączą wierzchołek z dokładnym środkiem boku, nie wymagają więc tworzenia kątów prostych.

Dodatkowo, środkowe odgrywają kluczową rolę w określaniu równowagi oraz środka ciężkości całej figury. Z kolei wysokości są nieodzowne do obliczania pola trójkąta i realizacji różnych wyliczeń geometrycznych związanych z kątem prostym. Choć obie te cechy mają różne zastosowania, każda z nich jest istotna w dziedzinie geometrii.

Jakie są praktyczne zastosowania wzoru na wysokość trójkąta?

Wzór na wysokość trójkąta znajduje szerokie zastosowanie zarówno w matematyce, jak i geometrii, ponieważ pozwala na precyzyjne wyliczenie wysokości, gdy znane są pole oraz długość podstawy. To w znaczący sposób upraszcza obliczenia związane z polem trójkąta w różnorodnych zadaniach matematycznych.

W dziedzinie inżynierii oraz budownictwa ta formuła odgrywa kluczową rolę w określaniu rozmiarów oraz analizie kształtów. Ma to istotne znaczenie w procesie projektowania i produkcji elementów o trójkątnym przekroju. Co więcej, wzór umożliwia badanie:

obwodu trójkąta,
symetrycznych właściwości,
zasad geometrycznych,
zastosowań w geometrii analitycznej,
aspektów planowania przestrzennego.

W edukacji, korzystając z tego wzoru, uczniowie mogą szybko rozwiązywać różne problemy geometryczne. To pozwala im lepiej zrozumieć związki pomiędzy bokami i kątami trójkąta, co z kolei w znaczący sposób poprawia ich umiejętności w obszarze matematyki i geometrii.