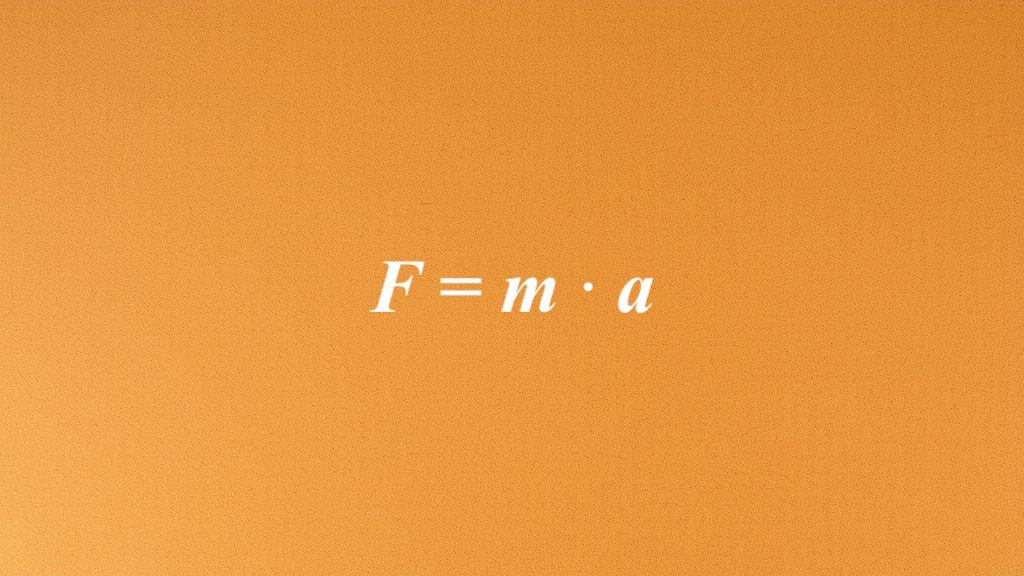Wzór na siłę

Siła to wektor, który ilustruje sposób, w jaki różne obiekty oddziałują na siebie, zarówno w ruchu, jak i w spoczynku. Aby obliczyć wartość siły, posługujemy się równaniem F = m ⋅ a, opartym na drugiej zasadzie dynamiki Newtona. Oznacza to, że siła, która działa na dany obiekt, jest wynikiem pomnożenia jego masy przez przyspieszenie, które ten obiekt osiąga w wyniku działania tej siły. Masa obiektu z kolei odzwierciedla jego bezwładność, a przyspieszenie wskazuje, jak zmienia się jego prędkość w czasie.

Siłę mierzy się w niutonach (N). Na przykład:

1 niuton to taka siła, która nadaje ciału o masie 1 kilograma przyspieszenie 1 metra na sekundę kwadratową,
to równanie jest fundamentalne w dynamice, umożliwiając analizę ruchu oraz przewidywanie zachowań obiektów pod wpływem różnych sił,
możemy rozwiązywać rozmaite problemy mechaniczne,
wspierać projektowanie różnorodnych urządzeń inżynieryjnych.

Jak brzmi wzór na siłę?

Wzór na siłę zapisuje się jako F = m ⋅ a. W tej formułce F reprezentuje siłę, m to masa obiektu, a a oznacza przyspieszenie, które ta masa osiąga. Zasada ta wywodzi się z drugiej reguły dynamiki Newtona i pozwala na obliczenie wartości siły oddziałującej na dany obiekt.

W praktyce siła jest ściśle związana z masą ciała oraz przyspieszeniem, które to powoduje. Wzór na siłę wypadkową wykorzystuje się do określenia łącznej siły działającej na dany obiekt, co jest równoważne sumie wszystkich działających na niego sił.

Znajomość tego wzoru jest niezwykle cenna w różnych dziedzinach, takich jak:

fizyka,
inżynieria,
sport.

Dokładne obliczenia siły umożliwiają nie tylko analizę ruchu, ale także ocenę wpływu różnych sił na obiekty.

Znaczenie symboli F, m, a w równaniu siły

Symbol F w równaniu F = m ⋅ a oznacza siłę, która jest wektorową wielkością fizyczną opisującą interakcje między różnymi ciałami. Symbol m reprezentuje masę, będącą skalarem, który mierzy ilość materii w danym obiekcie. Jest to wartość, która pozostaje stała. Z kolei symbol a odnosi się do przyspieszenia, definiowanego jako wektorowa zmiana prędkości obiektu w jednostce czasu.

Wzór na siłę ukazuje, że siła to produkt masy i przyspieszenia. To oznacza, że:

wzrost masy skutkuje powstaniem większej siły,
zwiększenie przyspieszenia również prowadzi do większej siły,
przy podnoszeniu ciężkiego przedmiotu wymagana jest znacznie większa siła,
w sytuacji gwałtownego przyspieszania potrzeba więcej siły,
wszystkie te czynniki mają wpływ na interakcje z obiektami.

Jednostka siły: czym jest niuton?

Niuton (N) stanowi jednostkę siły w systemie SI. Wyraża on siłę potrzebną do przyspieszenia obiektu o masie 1 kilograma o 1 metr na sekundę kwadrat (1 N = 1 kg · m/s²). Ta jednostka jest niezwykle ważna w dziedzinach takich jak fizyka i inżynieria, gdzie precyzyjne określenie wartości sił ma kluczowe znaczenie. Aby zmierzyć siłę w niutonach, wykorzystuje się siłomierz, który wskazuje, jaka siła działa na dany obiekt.

Jak II zasada dynamiki Newtona opisuje siłę?

II zasada dynamiki Newtona opisuje siłę jako iloczyn masy obiektu oraz przyspieszenia, które ten obiekt doświadcza. Możemy to ująć w prosty wzór: F = m ⋅ a, gdzie F oznacza siłę. Siła wprowadza zmiany w ruchu danego ciała, co z kolei prowadzi do jego przyspieszenia (a). Gdy pragniemy zwiększyć przyspieszenie obiektu o danej masie, konieczne jest zastosowanie większej siły.

Ważne punkty dotyczące zasady dynamiki:

siła jest iloczynem masy i przyspieszenia,
wzrost masy wymaga większej siły dla tego samego przyspieszenia,
jest kluczowa w analizie ruchu,
ma zastosowanie w obliczeniach sił w różnych układach fizycznych.

Ta podstawowa zasada dynamiki jest niezwykle istotna w analizie ruchu oraz w obliczeniach sił działających w różnych układach fizycznych.

Zależność między masą, przyspieszeniem a siłą

Związek między masą, przyspieszeniem a siłą można wykazać za pomocą prostego równania: F = m ⋅ a. To oznacza, że siła działająca na obiekt wynika z mnożenia jego masy przez przyspieszenie.

Masa, jako miara bezwładności, wskazuje na opór, jaki ciało stawia wobec zmian w swoim ruchu. Z kolei przyspieszenie definiuje, jak szybko zmienia się prędkość w określonym czasie. Im większa masa lub przyspieszenie, tym silniejsza siła jest wymagana, aby rozpocząć ruch ciała lub go zmienić.

Zrozumienie tej relacji jest istotne dla analizy sił i ruchu w fizyce. Daje to możliwość lepszego pojmowania, w jaki sposób siły oddziałują na przedmioty w naszym otoczeniu.

Jak przekształcać wzór na siłę?

Wzór na siłę, czyli F = m ⋅ a, można modyfikować, aby uzyskać inne wielkości fizyczne, gdy znamy przynajmniej dwie z nich. Na przykład, aby obliczyć przyspieszenie, wystarczy podzielić siłę przez masę: a = F / m. Z kolei, aby dowiedzieć się, jaką masę ma dany obiekt, wystarczy podzielić siłę przez przyspieszenie: m = F / a.

Te przekształcenia znacznie upraszczają szybkie określanie brakujących parametrów. Odgrywają one istotną rolę w analizie ruchu ciał oraz w rozwiązywaniu zadań z zakresu dynamiki. Dzięki tym umiejętnościom, można na przykład określić siłę działającą na obiekt lub masę na podstawie znanych wartości siły i przyspieszenia.

Owa wiedza jest nieoceniona w naukach ścisłych oraz inżynierii, gdzie precyzyjne obliczenia mają kluczowe znaczenie.

Siła wypadkowa i jej wzór

Siła wypadkowa to łączny wpływ wszystkich sił, które oddziałują na dane ciało. Można ją rozumieć jako sumę wektorów tych sił. To właśnie siła wypadkowa determinuje przyspieszenie oraz ewentualne zmiany w ruchu obiektu. Zgodnie z drugą zasadą dynamiki Newtona, wyraża się ona poprzez wzór F_w = ΣF, gdzie F_w oznacza siłę wypadkową, a ΣF to suma wszystkich działających na ciało sił.

Analizując to równanie, jesteśmy w stanie określić zarówno:

wartość siły,
kierunek całkowitej siły,
wpływ na obiekt w danym układzie.

Rozumienie siły wypadkowej jest niezbędne do tego, aby uchwycić zasady dynamiki ruchu. Co więcej, pozwala to na przewidywanie, jak obiekty zareagują na różnorodne zewnętrzne interakcje.

Definicja siły wypadkowej i suma wektorowa sił

Siła wypadkowa to nic innego jak wektorowa suma wszystkich oddziałujących na ciało sił. Zawiera zarówno ich wartości, jak i kierunki oraz zwroty. Innymi słowy, definicja siły wypadkowej podkreśla, że efekt działania wszystkich tych sił można zredukować do jednej, która wywołałaby identyczny wpływ na ruch obiektu.

Aby obliczyć siłę wypadkową, musimy dodać wektory sił. Kiedy te siły działają w kącie prostym do siebie, możemy skorzystać z twierdzenia Pitagorasa, by określić wielkość siły wynikowej. Znajomość tej zasady jest niezwykle istotna w fizyce, ponieważ umożliwia dokładną analizę ruchu różnych obiektów.

Jak określić kierunek i zwrot siły?

Kierunek oraz zwrot siły można zdefiniować za pomocą wektora siły, który przedstawia ją jako strzałkę. Ta strzałka jednoznacznie pokazuje, gdzie i w jakim kierunku działa siła. Jej kierunek wskazuje na linię działania, podczas gdy zwrot wyjaśnia, w którą stronę siła jest skierowana na tej linii.

Zrozumienie tych parametrów ma kluczowe znaczenie dla prawidłowego sumowania sił oraz analizy ruchu obiektów. Istnieje wiele metod, które mogą pomóc w precyzyjnym określeniu kierunku i zwrotu wektora siły, w tym:

techniki geometryczne, takie jak rysowanie wektorów,
podejścia analityczne, obejmujące rozkład siły na jej składowe,
wizualizacje używające narzędzi graficznych.

Dzięki tym różnorodnym metodom uzyskujemy dokładny obraz działania siły w danym układzie.

Metoda równoległoboku w analizie sił

Metoda równoległoboku to skuteczny sposób na graficzne określenie siły wypadkowej, gdy mamy do czynienia z dwiema siłami działającymi pod pewnym kątem. Aby to zobrazować, konstruujemy równoległobok, którego boki odpowiadają długościom tych wektorów. Przekątna równoległoboku z kolei wskazuje na wartość, kierunek i zwrot wynikowej siły.

Dzięki tej metodzie możemy łączyć zarówno wartości sił, jak i ich wzajemne ustawienie, co znacznie ułatwia analizę ruchu obiektów pod wpływem różnych sił. Równoległobok staje się szczególnie użyteczny, gdy siły nie są skierowane w tym samym kierunku, umożliwiając dokładne i graficzne obliczenie sumy wektorowej sił.

Siła ciężkości i przyspieszenie ziemskie

Siła ciężkości to naturalna moc, dzięki której Ziemia przyciąga wszystko, co ma masę. Możemy ją wyliczyć korzystając z równania Fg = m · g, gdzie „g” oznacza przyspieszenie ziemskie, wynoszące mniej więcej 9,81 m/s². Ta wartość jest stałą fizyczną, która definiuje intensywność pola grawitacyjnego naszej planety.

Siła ciężkości działa pionowo w dół, zmierzając ku środkowi Ziemi. Jest kluczowym elementem w analizie ruchu obiektów w grawitacyjnym środowisku. Zrozumienie tego zjawiska umożliwia nam precyzyjne określenie ciężaru różnych przedmiotów. Co więcej, jest ona niezwykle istotna w wielu dziedzinach, takich jak:

fizyka,
inżynieria,
budownictwo.

Jak obliczyć siłę ciężkości: Fg = m · g

Siła ciężkości może być obliczona za pomocą prostego wzoru: Fg = m · g. W tym równaniu:

m reprezentuje masę obiektu w kilogramach,
g to przyspieszenie ziemskie wynoszące około 9,81 m/s².

Aby określić wartość siły ciężkości, wystarczy pomnożyć masę przez przyspieszenie. Otrzymany wynik wyrażamy w niutonach (N).

Ten wzór stanowi fundamentalne narzędzie w fizyce, pomagając zrozumieć, jak Ziemia przyciąga różne masy. W kontekście dynamiki oraz w analizie ruchu ciał, kluczową rolę odgrywa wpływ grawitacji. Innymi słowy, pojęcie siły ciężkości jest niezbędne do podejmowania skutecznych badań nad ruchem obiektów na naszej planecie.

Czym jest ciężar i jak się go wyznacza?

Ciężar to siła, z jaką obiekt oddziałuje z podłożem lub zawieszeniem, a jego źródłem jest siła ciężkości. Możemy go obliczyć za pomocą wzoru Fg = m ⋅ g, gdzie:

m symbolizuje masę ciała,
g to przyspieszenie ziemskie, wynoszące około 9,81 m/s².

Jednostką ciężaru są niutony (N), ponieważ jest to siła. W przeciwieństwie do masy, która pozostaje stała i niezmienna w różnych warunkach, ciężar zmienia się w zależności od przyspieszenia ziemskiego. To sprawia, że jego wartość może różnić się w zależności od miejsca, na przykład na różnych planetach.

Najważniejsze rodzaje sił i ich wzory

W fizyce rozróżniamy kilka istotnych rodzajów sił, które odgrywają kluczową rolę w opisie ruchu oraz interakcji różnych obiektów. Na przykład, siła tarcia działa w przeciwnym kierunku do ruchu ciała. Jej wartość jest uzależniona od współczynnika tarcia oraz siły, z jaką obie powierzchnie na siebie oddziałują. Możemy to przedstawić za pomocą równania: F_t = μ ⋅ N, gdzie μ reprezentuje współczynnik tarcia, a N to siła nacisku.

Innym ważnym typem siły jest siła sprężystości, która posługuje się prawem Hooke’a. Ta siła może być opisana równaniem: F_s = -k ⋅ x, gdzie k to stała sprężystości, natomiast x odnosi się do odkształcenia sprężyny lub innego ciała sprężystego.

Gdy ciało porusza się po torze okręgu, mamy do czynienia z siłą dośrodkową. Możemy ją obliczyć, stosując wzór: F_c = m ⋅ v² / r. Tu m to masa ciała, v to jego prędkość liniowa, a r oznacza promień okręgu. Właściwością tej siły jest to, że zawsze kieruje się ku środkowi okręgu, co pozwala utrzymać ciało na zakrzywionym torze.

Kolejnym interesującym przypadkiem jest siła bezwładności. To siła pozorna, która występuje w układach nieinercjalnych i jest powiązana z przyspieszeniem danego układu odniesienia. Jej działanie sprawia, że ciała przeciwdziałają zmianom swojego ruchu.

Na zakończenie, siły elektromagnetyczne obejmują interakcje pomiędzy ładunkami elektrycznymi oraz magnetycznymi. Temat ten jest fundamentalny w fizyce i wymaga znajomości praw elektromagnetyzmu, aby je właściwie zrozumieć i opisać. Wszystkie wspomniane siły mają swoje odpowiednie równania, które pozwalają na precyzyjne obliczenia oraz analizę zjawisk fizycznych w różnych kontekstach.

Siła tarcia i wpływ współczynnika tarcia

Siła tarcia to zjawisko, które działa przeciwko ruchowi dwóch stykających się powierzchni. Można ją obliczyć, stosując wzór F_t = μ ⋅ N, gdzie μ oznacza współczynnik tarcia, a N to siła nacisku, która działa prostopadle do tych powierzchni.

Wartość współczynnika tarcia jest bezwymiarowa i zmienia się w zależności od rodzaju materiałów oraz ich powierzchni. Dla przykładu, wyższa wartość μ wskazuje na większe tarcie, co w praktyce utrudnia przesuwanie obiektów.

Siła tarcia odgrywa niezwykle istotną rolę w zachowaniu stabilności różnych mechanizmów oraz w zapewnieniu bezpieczeństwa urządzeń. Ma wpływ nie tylko na hamowanie, ale także na kontrolowanie ruchu. Dzięki obliczeniom opartym na współczynniku μ można dokładnie prognozować, jak będą się zachowywać ciała w kontakcie ze sobą.

Siła sprężystości (prawo Hooke’a)

Siła sprężystości działa w przeciwnym kierunku do odkształcenia ciała, które jest sprężyste. Zgodnie z prawem Hooke’a, można ją opisać za pomocą wzoru: F_s = -k ⋅ x. W tym równaniu:

F_s odnosi się do siły sprężystości,
k to stała sprężystości,
x symbolizuje przemieszczenie obiektu względem jego stanu równowagi.

Stała sprężystości, wyrażana w niutonach na metr (N/m), stanowi miarę sztywności materiału. Wyższa wartość k oznacza, że ciało stawia większy opór w obliczu odkształcenia.

Siła sprężystości odgrywa istotną rolę w mechanice ciał stałych. Jest niezwykle ważna, gdy analizujemy odkształcenia sprężyste, a także przy projektowaniu elementów, takich jak amortyzatory czy sprężyny.

Siła dośrodkowa przy ruchu po okręgu

Siła dośrodkowa występuje w przypadku obiektów poruszających się po okręgu, a jej kierunek zawsze prowadzi ku środkowi tego okręgu. Można ją obliczyć, stosując wzór: F_c = m ⋅ v² / r. W tej formule „m” oznacza masę obiektu, „v” to jego prędkość liniowa, a „r” to promień okręgu.

Bez siły dośrodkowej niemożliwe byłoby utrzymanie ciała na krzywym torze, ponieważ powoduje ona przyspieszenie dośrodkowe, które zmienia wyłącznie kierunek prędkości, nie wpływając na jej wielkość. Gdyby ta siła nie istniała, obiekt poruszałby się po linii prostej. Dlatego tak istotne jest uwzględnienie trzech podstawowych czynników:

masy,
prędkości,
promienia.

by precyzyjnie określić wartość siły dośrodkowej.

Siła bezwładności i jej rola w ruchu

Siła bezwładności to specyficzny fenomen, który ujawnia się w układach nieinercjalnych. Gdy obiekt przyspiesza, zaczyna odczuwać tę siłę, co jest bezpośrednio związane z jego bezwładnością – oporem masy na zmiany w ruchu.

To, jak masa ciała wpływa na jego bezwładność, jest niezwykle istotne. Zauważ, że:

większa masa wiąże się z większym oporem przy próbie przyspieszenia,
siła bezwładności odgrywa kluczową rolę w analizie ruchu obiektów w warunkach przyspieszonych,
pozwala lepiej wyjaśnić, jak zachowują się ciała w takich sytuacjach.

Warto jednak podkreślić, że siła bezwładności to nie siła w sensie fizycznym; to narzędzie wykorzystujące matematykę, które upraszcza opisywanie procesów w niestacjonarnych układach.

Oddziaływania elektromagnetyczne

Siły elektromagnetyczne stanowią fundamentalne oddziaływania, które zachodzą pomiędzy ładunkami elektrycznymi oraz polami magnetycznymi. Te siły oddziałują na naładowane cząstki, wpływając na ich ruch oraz zachowanie, niezależnie od tego, czy mówimy o atomach, czy o zjawiskach w skali makroskopowej.

W klasycznej fizyce prawo Coulomba precyzyjnie określa, jaką siłę odczuwają dwa punktowe ładunki elektryczne.

W nowoczesnym ujęciu elektromagnetyzmu, pola elektryczne i magnetyczne są ze sobą nierozerwalnie powiązane. To wyjątkowe połączenie jest kluczowe dla zrozumienia wielu zjawisk, takich jak:

prąd elektryczny,
indukcja magnetyczna,
fale elektromagnetyczne.

Dodatkowo, siły elekromagnetyczne należą do czterech podstawowych oddziaływań w przyrodzie, kształtując rozwój technologii, elektroniki oraz dziedziny fizyki jądrowej.

Moment siły i zmiana pędu

Moment siły to istotny parametr, który określa, jak siła oddziałuje na obrót obiektu wokół określonej osi. Można go zdefiniować jako iloczyn wektora siły oraz długości ramienia, które stanowi odległość między osią obrotu a punktem, w którym ta siła działa.

Pojęcie zmiany pędu, która powstaje jako wynik iloczynu masy i prędkości obiektu, jest bezpośrednio związane z działaniem siły. Zgodnie z zasadą dynamiki Newtona, siła jest równa pochodnej pędu w odniesieniu do czasu. Stąd wynika, że siła nie tylko wpływa na zmianę pędu, ale również na ruch liniowy oraz obrotowy obiektów.

Badanie momentu siły i zmian pędu jest kluczowe w dziedzinie mechaniki. Pomaga to zrozumieć zarówno przemieszczenia, jak i obroty, które są rezultatem działania różnorodnych sił.

Co to jest moment siły?

Moment siły to zdolność siły do powodowania obrotu wokół określonej osi lub punktu. Można go obliczyć poprzez pomnożenie wartości siły przez ramię siły, które jest prostopadłą odległością między działającą siłą a osią obrotu. To właśnie moment siły decyduje o tym, jak zmienia się ruch obrotowy obiektu. Co więcej, jest on niezwykle istotny w badaniach mechaniki ciał sztywnych.

Zależność między siłą a zmianą pędu

Związek między siłą a pędem można zdefiniować za pomocą równania, w którym siła stanowi pochodną pędu w odniesieniu do czasu. Pęd to wartość uzyskiwana przez mnożenie masy ciała i jego prędkości. W skrócie, jakakolwiek zmiana w prędkości, a tym samym w pędzie, wymaga zastosowania siły. Ta zasada leży u podstaw drugiej zasady dynamiki Newtona.

W codziennym zastosowaniu oznacza to, że siła wywierana na obiekt prowadzi do jego przyspieszenia. Zmiany te mogą dotyczyć zarówno wartości, jak i kierunku pędu. Takie podejście pozwala na dokładną analizę ruchu obiektów pod wpływem różnorodnych sił. Dzięki niemu jesteśmy w stanie uwzględnić zmiany prędkości oraz masy w bardziej skomplikowanych sytuacjach.

Obliczanie siły w praktyce

Obliczenia dotyczące siły w praktyce opierają się na równaniu F = m ⋅ a, w którym F oznacza siłę, m jest masą obiektu, a a to przyspieszenie. W kontekście dynamiki istotne jest, aby dokładnie przeanalizować wszystkie siły działające na dany przedmiot oraz obliczyć siłę wypadkową, będącą wektorową sumą tych sił.

Na przykład, aby obliczyć siłę działającą na pojazd o masie 1000 kg przy przyspieszeniu wynoszącym 2 m/s², wystarczy pomnożyć masę przez wartość przyspieszenia. W rezultacie uzyskujemy siłę równą 2000 niutonom (N).

Dzięki znajomości różnych typów sił, takich jak:

tarcie,
ciężkość,
siły sprężyste,
siły elektromagnetyczne,
siły grawitacyjne.

możemy lepiej modelować rzeczywiste scenariusze. W praktyce obliczenia siły mają kluczowe znaczenie w takich dziedzinach, jak projektowanie stabilnych budynków czy optymalizacja metod treningowych w sporcie. Analizując wpływ sił, możemy zwiększać efektywność ruchu i dbać o bezpieczeństwo sportowców.

Poprawne wykorzystanie wzoru na siłę umożliwia przewidywanie reakcji ciał na działające na nie siły. To podejście jest także pomocne w rozwiązywaniu problemów zarówno w fizyce, jak i w inżynierii.

Jak rozwiązać zadania z dynamiki?

Rozwiązywanie problemów z zakresu dynamiki zaczyna się od zidentyfikowania wszystkich sił oddziałujących na dane ciało. Do tych sił zaliczamy często:

siłę ciężkości,
siłę tarcia,
siłę sprężystości.

Następnym krokiem jest obliczenie siły wypadkowej, co można zrobić na kilka sposobów, między innymi poprzez zastosowanie metody równoległoboku lub suma wektorową.

Kiedy już mamy siłę wypadkową, korzystamy z równania F = m ⋅ a. W tym równaniu F to siła wypadkowa, m oznacza masę ciała, a a to jego przyspieszenie. Warto również zwrócić uwagę na kierunek oraz zwrot tych sił, ponieważ jest to kluczowe dla pełnego zrozumienia ruchu obiektu.

Metody graficzne oraz analityczne odgrywają istotną rolę w tym procesie. Oferują one dokładne obliczenia oraz upraszczają analizę ruchu w zadaniach dotyczących dynamiki, co z pewnością ułatwia zrozumienie tego zagadnienia.

Przykłady zastosowania wzoru na siłę w życiu codziennym

Siła ma wiele praktycznych zastosowań w naszym codziennym życiu. Na przykład:

w branży budowlanej, jej znajomość jest niezbędna do projektowania solidnych i bezpiecznych struktur, takich jak budynki i mosty,
w sporcie, zasady dotyczące siły pomagają w lepszej analizie ruchów zawodników,
w kontekście pojazdów i maszyn, zasady siły pozwalają ocenić siły, które na nie działają.

Inżynierowie analizują różne siły, które oddziałują na poszczególne elementy konstrukcji, co pozwala unikać uszkodzeń spowodowanych ciężarem czy wiatrem. Dodatkowo, dzięki tym samym zasadom możliwe jest doskonalenie technik oraz zwiększanie efektywności treningów. To z kolei ma ogromny wpływ na stabilność oraz bezpieczeństwo użytkowania tych urządzeń.

Nie można zapominać, że znajomość wzoru na siłę to fundamentalne narzędzie w wielu dziedzinach praktycznych.

Związek siły z energią mechaniczną

Siła ma bezpośredni wpływ na energię mechaniczną, w szczególności na energię kinetyczną obiektów. Ta ostatnia jest uzależniona od:

masy obiektu,
kwadratu prędkości danego ciała.

Kiedy siła wykonuje pracę, następuje zmiana tej energii. Można to ująć w prosty sposób: praca siły to iloczyn jej wartości, przesunięcia obiektu oraz cosinusa kąta między nimi. Takie działanie prowadzi do wzrostu lub spadku energii kinetycznej.

W odniesieniu do zasady zachowania energii mechanicznej, stwierdza ona, że w zamkniętym układzie całkowita energia mechaniczna, czyli suma energii kinetycznej i potencjalnej, pozostaje stała. Dzięki tej zasadzie jesteśmy w stanie obliczać siły, biorąc pod uwagę zmiany energii podczas ruchu, co jest istotne przy analizie dynamiki w fizyce.

Relacja między siłą a energią mechaniczną umożliwia precyzyjne opisanie ruchu ciała oraz jego interakcji w otaczającym świecie.

Energia kinetyczna a praca wykonana przez siłę

Energia kinetyczna odnosi się do energii, którą posiada obiekt w ruchu. Możemy ją obliczyć, korzystając z prostego wzoru: E_k = ½ m v², gdzie m symbolizuje masę obiektu, a v jego prędkość.

Gdy na ciało działa siła, wykonuje ona pracę, która prowadzi do zmiany jego energii kinetycznej. Pracę, oznaczaną literą W, można obliczyć, mnożąc siłę (F) przez przesunięcie (s) oraz cosinus kąta (θ) między kierunkiem siły a przesunięciem:

W = F · s · cos θ.

Na przykład, jeśli siła działa w tym samym kierunku co ruch obiektu, cała praca przyczyni się do zwiększenia jego energii kinetycznej. To pokazuje, jak ściśle energia kinetyczna jest powiązana z pracą wykonaną przez siłę. Ta zależność odgrywa istotną rolę w badaniu dynamiki ruchu.

Jak zasada zachowania energii odnosi się do obliczania siły?

Zasada zachowania energii umożliwia nam obliczanie siły poprzez badanie zmian energii mechanicznej obiektu. W zamkniętym układzie mechanika energia pozostaje na stałym poziomie. Siła, która wykonuje pracę, prowadzi do modyfikacji energii kinetycznej lub potencjalnej.

Na przykład, gdy znamy wielkość pracy, jaką wykonano, oraz przemieszczenie, możemy łatwo obliczyć siłę, posługując się równaniem:

praca = siła × droga.

Takie obliczenia siły opierają się nie tylko na znanych wzorach z dynamiki, ale także na równowadze energii mechanicznej.

Kiedy stosuje się wzór na siłę?

Wzór na siłę jest przydatnym narzędziem, gdy mamy do czynienia z masą ciała oraz jego przyspieszeniem, a chcemy określić siłę, która na nie działa. To kluczowe zastosowanie wzoru pojawia się w fizyce, zwłaszcza w kontekście analizy ruchu obiektów oraz ich interakcji.

Na przykład, w budownictwie wykorzystanie tego wzoru jest istotne przy projektowaniu konstrukcji. Elementy budowlane muszą bowiem wytrzymać konkretne obciążenia oraz siły oddziałujące na obiekty, takie jak:

budynki,
mosty,
inne konstrukcje.

W sporcie z kolei analiza siły umożliwia doskonalenie techniki ruchu, co przekłada się na zwiększenie efektywności oraz bezpieczeństwa podczas treningów.

Co więcej, wzór na siłę ma charakter uniwersalny. Stosuje się go w różnych dziedzinach nauki i techniki, gdzie istotne jest zrozumienie oraz dokładne obliczenie sił, które oddziałują na obiekty.

Sytuacje praktyczne: fizyka, budownictwo, sport

Wzór na siłę ma wiele praktycznych zastosowań w różnych obszarach. Oto kilka kluczowych dziedzin, w których zastosowanie wzoru przynosi realne korzyści:

w fizyce umożliwia dokładną analizę ruchu ciał i ich wzajemnych oddziaływań, co jest kluczowe w badaniach nad dynamiką,
w budownictwie jego znajomość przydaje się do obliczania obciążeń działających na konstrukcje, co pozwala na projektowanie bezpiecznych i trwałych budynków oraz mostów,
w sporcie wspiera optymalizację techniki, co zwiększa efektywność siły mięśniowej,
w inżynierii wpływa na bezpieczeństwo oraz wydajność maszyn i pojazdów.

Te różne zastosowania pokazują, jak istotny jest wzór na siłę w rozwiązywaniu praktycznych problemów i w poprawie funkcjonowania wielu systemów.