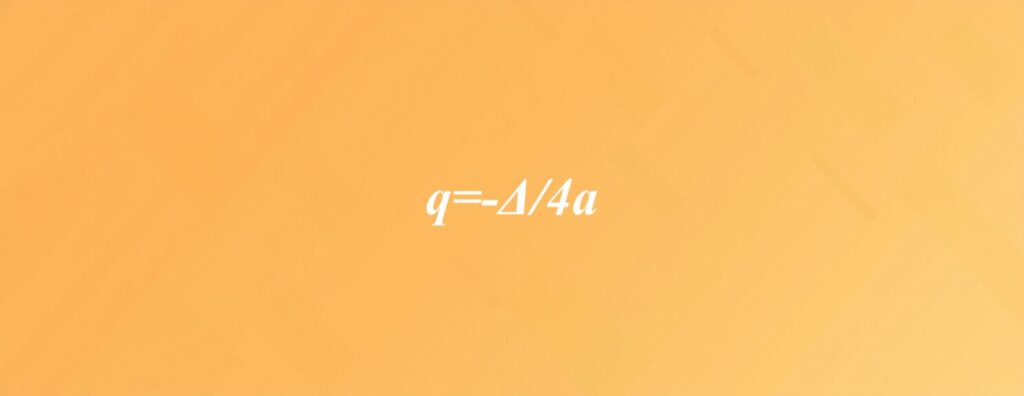Wzór na q

Co to jest wzór na q w funkcji kwadratowej?

Wzór na parametr q w kontekście funkcji kwadratowej stanowi kluczowy element jej analizy, zwłaszcza gdy rozważamy jej postać kanoniczną. Możemy go zapisać jako q = -Δ/(4a), gdzie Δ oznacza wyróżnik, a a to współczynnik przy x². To zrozumienie q pozwala nam określić współrzędną y wierzchołka paraboli, co z kolei pomaga w lepszym uchwyceniu miejsca oraz kształtu wykresu.

W postaci kanonicznej funkcji, przedstawionej jako y = a(x – p)² + q, wartości p i q wyznaczają położenie wierzchołka parabol. Co więcej, q dostarcza informacji o wysokości tego wierzchołka, której kształt jest powiązany z wartością współczynnika a oraz wyróżnika Δ. Zrozumienie tej zależności znacząco upraszcza analizę funkcji oraz pozwala określić, w którą stronę kieruje się parabola – czy ku górze, czy ku dołowi.

Rola wzoru na q wykracza poza obliczenia wysokości wierzchołka i ma istotne znaczenie w szerszej ocenie zachowań funkcji kwadratowych. Dzięki temu wzorowi możemy przewidywać, jakie wartości mogą przyjmować różne funkcje, co jest istotne w różnych dziedzinach matematyki, w tym:

• geometrze analitycznej,
• optymalizacji,
• analizie miejsc zerowych funkcji kwadratowej.

Należy również podkreślić, że wzór na q ułatwia analizowanie miejsc zerowych funkcji kwadratowej, ukazując istotne powiązania między q, Δ i wykresem parabol.

Jakie są postacie funkcji kwadratowej?

Postać ogólna

Ogólna postać funkcji kwadratowej firma się równaniem y = ax² + bx + c, gdzie a, b i c to współczynniki rzeczywiste, przy czym a nie może wynosić zero. Jest to podstawowy model matematyczny, który stanowi punkt wyjścia do analizy funkcji kwadratowych. Wartość współczynnika a ma kluczowe znaczenie dla kształtu paraboli:

• gdy a jest większe od zera, ramiona paraboli kierują się ku górze,
• natomiast kiedy a jest mniejsze od zera, ramiona zwrócone są w dół.

Dzięki ogólnej postaci możemy również obliczyć wyróżnik Δ, co jest niezwykle pomocne w poszukiwaniu miejsc zerowych tej funkcji. Miejsca zerowe, czyli wartości x, dla których y = 0, są istotne w wielu zastosowaniach matematycznych i praktycznych, a ich identyfikacja otwiera drzwi do dalszej analizy.

Zrozumienie ogólnej formy funkcji kwadratowej jest kluczowe dla badania parabol. Umożliwia to ich zastosowanie w rozmaitych dziedzinach, od geometrii po zagadnienia fizyczne. Co więcej, znajomość tych właściwości może być bardzo użyteczna w codziennym życiu, oferując nam narzędzia do lepszego zrozumienia otaczającego nas świata.

Postać kanoniczna z q

Postać kanoniczna funkcji kwadratowej, wyrażona jako y = a(x – p)² + q, odgrywa niezwykle ważną rolę w analizie wykresów parabol. Współrzędne wierzchołka (p, q) dostarczają informacji o położeniu paraboli w układzie współrzędnych. O ile q wskazuje na pionową lokalizację wierzchołka i można ją obliczyć za pomocą wzoru q = -Δ/(4a), gdzie Δ to wyróżnik funkcji kwadratowej.

• zrozumienie kształtu paraboli,
• identyfikacja ekstremalnych punktów,
• analiza zachowania funkcji kwadratowej,
• wizualizacja wykresu,
• zastosowanie w modelowaniu matematycznym.

Analiza graficzna z wykorzystaniem postaci kanonicznej znajduje zastosowanie w różnych obszarach matematyki, w tym w modelowaniu oraz rozwiązywaniu różnorodnych problemów.

Zrozumienie postaci kanonicznej, szczególnie wartości q, stanowi klucz do skutecznej analizy funkcji kwadratowej. Dlatego też, jest to niezastąpione narzędzie zarówno w geometrii, jak i w matematyce stosowanej.

Postać iloczynowa

Postać iloczynowa funkcji kwadratowej przyjmuje formę y = a(x – x₁)(x – x₂). W tym równaniu x₁ i x₂ reprezentują miejsca zerowe funkcji. Taki zapis jest szczególnie użyteczny, gdy wyróżnik Δ jest nie mniejszy od zera, co wskazuje, że funkcja posiada rzeczywiste pierwiastki.

Dzięki postaci iloczynowej z łatwością możemy zidentyfikować punkt, w którym funkcja przecina oś x. To znacząco ułatwia analizę jej zachowań w pobliżu tych miejsc. Na przykład, kiedy pierwiastki x₁ i x₂ wynoszą odpowiednio 2 i 5, możemy przedstawić funkcję w postaci y = a(x – 2)(x – 5).

Z punktu widzenia analizy graficznej, ta forma jest niezwykle użyteczna. Pozwala na szybką identyfikację miejsc zerowych i ustalenie, w którą stronę otwiera się parabola — w górę, gdy a > 0, lub w dół, gdy a < 0. To dobra alternatywa dla postaci ogólnej i kanonicznej, oferując równoważne podejście do problemu.

Jak obliczyć q w funkcji kwadratowej?

Obliczanie współrzędnej q w kontekście funkcji kwadratowej stanowi fundamentalny etap w badaniu parabol. Wartość ta odpowiada y-wierzchołkowi paraboli i można ją uzyskać ze wzoru q = -Δ/(4a), gdzie Δ symbolizuje wyróżnik funkcji kwadratowej, a a to współczynnik przy x².

Aby obliczyć wyróżnik Δ, posługujemy się formułą Δ = b² – 4ac, w której b oraz c to odpowiednio współczynniki przy x oraz wyraz wolny. Wartość Δ ma istotne znaczenie, ponieważ determinuje liczbę miejsc zerowych funkcji kwadratowej, co pomaga w określeniu położenia paraboli w układzie współrzędnych.

Współrzędna q wskazuje, czy funkcja kwadratowa osiąga maksimum, czy minimum. Gdy a > 0, parabola otwiera się ku górze, co oznacza, że q reprezentuje wartość minimalną. Natomiast w przypadku a < 0, parabola zwrócona jest w dół, co sprawia, że q staje się wartością maksymalną.

Obliczenie q jest niezbędne dla zrozumienia kształtu oraz rozmieszczenia paraboli. Dodatkowo, pozwala na analizę wykresu funkcji kwadratowej. Dzięki wzorowi na q, jesteśmy w stanie szybko określić kluczowe parametry funkcji, co stanowi podstawę do kolejnych, głębszych analiz matematycznych.

Wzór q = -Δ/4a

Wzór q = -Δ/(4a) umożliwia obliczenie współrzędnej y wierzchołka parabolicznego dla funkcji kwadratowej. Δ, nazywane wyróżnikiem, obliczamy z pomocą formuły Δ = b² – 4ac. W tej równaniu b to współczynnik przy x, natomiast c to wartość wolna. Parametr a odnosi się do współczynnika stojącego przed x² w danej funkcji kwadratowej.

Zastosowanie wzoru q = -Δ/(4a) jest niezwykle istotne, ponieważ pozwala zrozumieć, jak kształtuje się parabola, a także określić wysokość jej wierzchołka. Ta wartość informuje nas, czy dany punkt jest maksimum czy minimum. Dla funkcji kwadratowej otwierającej się ku górze (a > 0), q wskazuje na najniższy punkt, z kolei dla funkcji otwierającej się w dół (a < 0) oznacza najwyższy punkt.

Przykładowo, analizując funkcję f(x) = 2x² + 4x + 1, najpierw obliczamy wyróżnik: Δ = 4² – 4*2*1 = 4. Następnie możemy wyznaczyć q: q = -4/(4*2) = -0.5. Ostatecznie, wysokość wierzchołka tej funkcji wynosi -0.5, co jest istotne przy badaniu kształtu wykresu.

W praktyce, znajomość wzoru q = -Δ/(4a) stanowi cenną pomoc w rozwiązywaniu problemów związanych z ekstremami funkcji kwadratowej oraz podczas analizy geometrycznej wykresu.

Dlaczego delta ma znaczenie dla q?

Wartość delty (Δ) w kontekście funkcji kwadratowej jest niezwykle istotna, ponieważ pomaga ustalić współrzędną q, która z kolei wpływa na położenie wierzchołka paraboli. Wzór q = -Δ/(4a) pokazuje, w jaki sposób delta, która jest obliczana jako Δ = b² – 4ac, bezpośrednio oddziałuje na wartość y w punkcie wierzchołka.

Gdy wartość Δ jest dodatnia, możemy mówić o:

• dwu miejscach zerowych,
• różnych wartościach q – zarówno wyższych, jak i niższych,
• współzależności z parametrem a.

Kiedy Δ wynosi zero, parabola styka się z osią x, co skutkuje tym, że jej wierzchołek leży dokładnie na tej osi. Natomiast, w przypadku gdy delta jest ujemna, brak miejsc zerowych sprawia, że wierzchołek znajduje się albo powyżej, albo poniżej osi x.

Co więcej, w sytuacji, gdy delta przyjmuje wysokie wartości, zmiany w położeniu wierzchołka stają się bardziej zauważalne, co z kolei wpływa na kształt paraboli. Dlatego zrozumienie roli delty ułatwia interpretację paraboli i umożliwia prowadzenie bardziej zaawansowanych analiz funkcji kwadratowej, które mają zastosowanie nie tylko w matematyce, ale i w wielu innych dziedzinach.

Jaką rolę q odgrywa przy wierzchołku paraboli?

Parametr q w kontekście funkcji kwadratowej pełni niezwykle ważną rolę, ponieważ determinuje wysokość wierzchołka paraboli. Współrzędne wierzchołka, oznaczane jako (p, q), są określone w kanonicznej formie funkcji. Dzięki temu łatwiejsze staje się zrozumienie, jak wygląda wykres. Kiedy funkcję zapiszemy w postaci y = a(x – p)² + q, wartość q reprezentuje funkcję w wierzchołku, który stanowi kluczowy punkt ekstremalny.

Związek między parametrem q a pozycją wierzchołka jest wyraźny:

• kiedy q ma wartość dodatnią, wierzchołek unosi się powyżej osi x, co sugeruje, że w tym miejscu funkcja osiąga swoje minimalne wartości,
• ujemne q sprawia, że wierzchołek znajduje się poniżej osi x, co z kolei wskazuje na maksymalne wartości funkcji wokół tego punktu.

Aby skutecznie analizować maksimum i minimum funkcji kwadratowej, kluczowe jest zrozumienie, jak parameter q wpływa na kształt oraz lokalizację paraboli. Wartości q nie tylko informują nas o wysokości lub niskiej pozycji wierzchołka, lecz także decydują o ogólnym charakterze wykresu i jego graficznej interpretacji.

Współrzędne wierzchołka (p, q)

Współrzędne wierzchołka paraboli odgrywają kluczową rolę w badaniu funkcji kwadratowej. Są one reprezentowane przez punkt (p, q). Obliczenie wartości p oraz q odbywa się za pomocą poniższych wzorów:

• p = -b/(2a),
• q = -Δ/(4a),
• Δ = b² – 4ac.

Wierzchołek leży na osi symetrii paraboli i wyznacza ekstremum funkcji kwadratowej. Wysokość q bezpośrednio wpływa na położenie wierzchołka na osi y, co z kolei determinuje, czy funkcja ma minimum, czy maksimum, w zależności od kierunku otwarcia paraboli.

Zrozumienie współrzędnych (p, q) jest niezwykle istotne, aby móc przekształcić funkcję kwadratową do jej postaci kanonicznej. Ta forma znacząco ułatwia analizę i pozwala na lepszą wizualizację funkcji na wykresie. Dzięki temu możemy dostrzec, jak wartości funkcji zmieniają się w różnych przedziałach x. To zrozumienie ma ogromne znaczenie zarówno w teorii matematycznej, jak i w praktycznych zastosowaniach.

Jak q wpływa na wysokość wierzchołka?

Wartość q w funkcji kwadratowej ma fundamentalne znaczenie dla określenia pozycji wierzchołka paraboli. Możemy ją zdefiniować jako wynik funkcji w określonym punkcie p, co zapisujemy jako q = f(p). Taki zapis oznacza, że wartość q ma bezpośredni wpływ na to, gdzie wierzchołek znajdzie się na osi y.

Gdy współczynnik a jest większy od zera, wartość q osiąga minimum, co oznacza, że wierzchołek paraboli znajduje się w najniższym punkcie. Natomiast kiedy a jest mniejsze od zera, q staje się maksymalna, co sprawia, że wierzchołek znajduje się na górze paraboli.

Zmiany w wartości q mają wpływ na przesunięcie całego wykresu w górę lub w dół, co jest kluczowym elementem analizy graficznej funkcji kwadratowej. Obserwując, jak zmienia się wartość q, jesteśmy w stanie przewidzieć, w jaki sposób wykres będzie się kształtował. W kontekście funkcji kwadratowej zrozumienie położenia wierzchołka jest niezwykle istotne, ponieważ wpływa na ekstremalne wartości funkcji, co ma znaczenie w matematycznej analizie.

Jakie znaczenie ma q dla kształtu i położenia paraboli?

Parametr q w funkcji kwadratowej odgrywa fundamentalną rolę w określaniu położenia oraz kształtu paraboli. Wskazuje on na przesunięcie pionowe wykresu wzdłuż osi y, co pozwala na ustalenie miejsca, gdzie znajduje się wierzchołek paraboli. W rezultacie, ma to decydujący wpływ na to, czy funkcja osiąga wartość minimalną, czy maksymalną.

Przykładowo:

• gdy q jest wartością dodatnią, wierzchołek paraboli ulokowany jest powyżej osi x, co oznacza, że to w tym punkcie znajduje się jej minimalna wartość,
• gdy q jest ujemne, wykres przesuwa się w dół, sugerując tym samym, że funkcja może mieć maksymalną wartość.

Warto pamiętać, że zmiany w parametrze q nie wpływają na kształt ramion paraboli – to zależy od wartości parametru a. Ramiona pozostają niezmienne:

• wznoszą się, gdy a przyjmuje wartość dodatnią,
• opadają, gdy a jest ujemne.

Z tego powodu, pomimo ich stałości, geometrię paraboli warto dokładnie analizować. Zrozumienie wartości q jest zatem kluczowe dla całościowej analizy funkcji kwadratowej.

Analizując parametr q, zyskujemy także lepsze zrozumienie graficznego zachowania wykresu funkcji kwadratowej. Umożliwia to dostrzeganie trzech istotnych cech:

• minimalna wartość,
• maksymalna wartość,
• ogólne położenie wykresu w przestrzeni.

Dlatego uwzględnienie q w każdej analizie funkcji kwadratowej jest niezwykle istotne.

Jak q wpływa na minimalną i maksymalną wartość funkcji?

Wartość q w funkcji kwadratowej odgrywa istotną rolę w określaniu, czy mamy do czynienia z wartością minimalną, czy maksymalną funkcji. Gdy funkcja kwadratowa przyjmuje postać kanoniczną, wierzchołek paraboli znajduje się w punkcie o współrzędnych (p, q), gdzie q oznacza wartość funkcji w tym szczególnym miejscu.

• jeśli współczynnik a jest dodatni, parabola otwiera się w górę, a q staje się minimalną wartością funkcji,
• natomiast w sytuacji, gdy a jest ujemny, kształt paraboli skierowany jest w dół, co powoduje, że q osiąga wartość maksymalną.

Ostatecznie, wartość q definiuje ekstremum funkcji – jest to punkt, w którym wykres paraboliczny dociera do najwyższego lub najniższego poziomu. Zrozumienie, czym jest q, jest kluczowe dla analizy graficznej funkcji kwadratowej. Dzięki tej wiedzy można określić, czy funkcja dysponuje punktem maksimum, czy minimum, co ma istotne znaczenie w kontekście zagadnień optymalizacyjnych.

Co więcej, zmiany w wartości q wpływają na usytuowanie wierzchołka paraboli na płaszczyźnie współrzędnych, co z kolei kształtuje ogólną formę wykresu funkcji kwadratowej. W zastosowaniach matematycznych zrozumienie, jak q oddziałuje na wartości minimalne i maksymalne funkcji, pozwala na bardziej wnikliwą analizę i interpretację uzyskanych wyników.

Wpływ q na analizę graficzną wykresu

Wpływ parametru q na graficzną analizę wykresu funkcji kwadratowej jest niezwykle istotny. Dzięki niemu łatwiej zrozumieć, gdzie dokładnie znajduje się parabola oraz jakie są jej zachowania. Ten parametr przesuwa wykres w pionie, co bezpośrednio oddziałuje na wysokość wierzchołka paraboli, którego współrzędne można określić jako (p, q).

Zmiana wartości q nie wpływa na kształt paraboli, lecz jedynie na jej położenie – może przesuwać ją w górę lub w dół. Jest to ważne podczas tworzenia wykresu, ponieważ pozwala na jasne określenie, czy funkcja osiąga swoje ekstremalne wartości, jak minima czy maksima, w danym przedziale.

W kontekście analizy graficznej zrozumienie parametru q znacznie ułatwia interpretację funkcji oraz jej wartości na różnych odcinkach. Przykładowo, gdy funkcja kwadratowa osiąga minimum, zwiększenie wartości q przesuwa cały wykres w górę, co wpływa na wartość tego minimum. Analogicznie, obniżenie q skutkuje przesunięciem wykresu w dół, co z kolei prowadzi do wzrostu wartości maksymalnej.

Warto zatem podkreślić, że parametr q odgrywa kluczową rolę w analizie graficznej. Umożliwia on określenie, jak oraz gdzie parabola znajduje się na układzie współrzędnych. Tego rodzaju wiedza jest niezbędna do przeprowadzenia dalszych obliczeń oraz interpretacji wykresu funkcji kwadratowej.

Czy wzór na q pomaga znaleźć miejsca zerowe funkcji?

Wzór na q, mimo że nie służy bezpośrednio do odnajdywania miejsc zerowych funkcji kwadratowej, odgrywa kluczową rolę w ich analizie. Przede wszystkim q jest ściśle powiązane z wyróżnikiem Δ, który z kolei określa liczbę oraz rodzaj miejsc zerowych równania kwadratowego.

Miejsca zerowe funkcji kwadratowej można wyznaczyć z równania w postaci ax² + bx + c = 0. Wyniki tego równania, znane jako pierwiastki, są uzależnione od wartości wyróżnika Δ, obliczanego według formuły Δ = b² – 4ac. Kiedy Δ jest większe od zera, funkcja dysponuje:

• dwoma różnymi miejscami zerowymi,
• jednym podwójnym miejscem zerowym, gdy Δ wynosi zero,
• brakiem miejsc zerowych w zbiorze liczb rzeczywistych, gdy Δ jest mniejsze od zera.

Wzory Viete’a tworzą interesującą więź między miejscami zerowymi a współczynnikami równania kwadratowego. Dla miejsc zerowych x₁ i x₂ Viete’a stwierdza, że ich suma to x₁ + x₂ = -b/a, podczas gdy ich iloczyn można wyrazić jako x₁ · x₂ = c/a.

Chociaż wzór na q umożliwia ustalenie położenia wierzchołka paraboli, jego znaczenie wykracza poza tę funkcję. Ksztalt oraz usytuowanie paraboli wpływają na analizę miejsc zerowych. W rezultacie wzór na q może być używany jako narzędzie, które ułatwia zrozumienie, jak kształtuje się charakter wykresu funkcji kwadratowej oraz jak powiązane są z nim miejsca zerowe.

Zależność między q, deltą a miejscami zerowymi

Związek między wartością q, deltǫ a miejscami zerowymi funkcji kwadratowej to istotny aspekt jej analizy. Wartość q, która wskazuje na współrzędną wierzchołka paraboli, jest ściśle powiązana z wyróżnikiem Δ równania kwadratowego. Obliczamy go za pomocą formuły: Δ = b² – 4ac.

Warto również zwrócić uwagę na znaczenie delty w kontekście miejsc zerowych. Gdy Δ jest większe od zera (Δ > 0), funkcja kwadratowa posiada dwa oddzielne miejsca zerowe. Możemy je znaleźć, korzystając z odpowiednich wzorów pierwiastków:

• x₁ = (-b – √Δ) / (2a),
• x₂ = (-b + √Δ) / (2a).

Gdy Δ osiąga wartość zerową (Δ = 0), oznacza to, że parabola styka się z osią x w jednym punkcie, co skutkuje posiadaniem jednego miejsca zerowego. Z kolei, gdy Δ jest ujemne (Δ < 0), funkcja nie dysponuje rzeczywistymi miejscami zerowymi, co wskazuje, że parabola ani nie przecina osi x, ani nie zbliża się do niej.

Równanie q = -Δ/(4a) ilustruje, że wartość q jest uzależniona od delty i współczynnika a. Analizując q, zyskujemy lepsze pojęcie o lokalizacji wierzchołka paraboli względem miejsc zerowych. Ta wiedza jest niezbędna do efektywnej wizualizacji wykresów funkcji kwadratowej, a także do prowadzenia dalszych matematycznych analiz.

Wzory Viete’a a położenie paraboli

Wzory Viete’a odgrywają kluczową rolę w badaniu funkcji kwadratowych, umożliwiając zrozumienie związku między miejscami zerowymi równania a jego współczynnikami. Na mocy tych wzorów:

• suma miejsc zerowych (x₁ + x₂) równa się -b/a,
• iloczyn miejsc zerowych (x₁·x₂) to c/a.

Dzięki tym relacjom łatwiej jest pojąć, w jaki sposób te wartości wpływają na usytuowanie paraboli na osi x oraz na wartość q, co z kolei determinuje wysokość wierzchołka.

Wartość q ma znaczący wpływ na położenie paraboli na osi y. Gdy q ulega zmianie, również wysokość wierzchołka ulega modyfikacjom. Miejsca zerowe, będące rozwiązaniami równania kwadratowego, to dokładnie te punkty, w których parabola interaktywnie styka się z osią x. Zmiany w q kształtują zarówno położenie, jak i formę paraboli, co jest niezwykle istotne podczas analizy wykresu.

Dzięki prostocie wzorów Viete’a, można szybko zrozumieć, jak zmiany miejsc zerowych wpływają na kształt i usytuowanie paraboli. Analiza miejsc zerowych oraz ich związków z wartością q przyczynia się do głębszego poznania funkcji kwadratowej, co znacznie ułatwia interpretację jej wykresu.

Kiedy warto wykorzystać wzór na q w analizie funkcji kwadratowej?

Wzór na q w kontekście analizy funkcji kwadratowej ma ogromne znaczenie. Jest kluczowy dla określenia, gdzie znajduje się wierzchołek paraboli oraz do badania ekstremów tych funkcji. Dzięki znajomości tego wzoru łatwiej przechodzi się między różnymi postaciami funkcji kwadratowej, co z kolei przyczynia się do lepszego zrozumienia ich właściwości.

W szczególności, zastosowanie wzoru na q ma dużą wagę podczas analizy graficznej. Umożliwia szybkie wychwycenie wartości minimalnych i maksymalnych funkcji. Co więcej, daje możliwość określenia, jak zmieniają się kształt oraz położenie paraboli w zależności od parametrów a, b i c.

Na przykład, wzór na q jest przydatny w zadaniach dotyczących geometrii wykresów, gdzie istotne jest dokładne wyznaczenie punktów przecięcia z osią Y. Dodatkowo, w kontekście optymalizacji, ten wzór jest pomocny w ustaleniu warunków sprzyjających osiągnięciu ekstremum. To czyni go niezwykle wartościowym narzędziem w praktycznych zastosowaniach, takich jak zarządzanie produkcją czy ekonomia.

W skrócie, wzór na q to nie tylko sposób na określenie parametrów funkcji kwadratowej, ale również ważne wsparcie dla geometrii wykresów, co czyni go niezastąpionym elementem w analizie funkcji kwadratowych.

Przykłady zastosowania q w zadaniach matematycznych

Parametr q w funkcji kwadratowej odgrywa kluczową rolę w wielu obszarach matematyki, a jego zastosowanie jest niezwykle wszechstronne. Oto kilka sposobów, w które można wykorzystać q:

• Wyznaczanie ekstremów: dzięki wzorowi na q, możemy szybko określić zarówno maksymalne, jak i minimalne wartości funkcji kwadratowej, co czyni go niezastąpionym narzędziem w zadaniach optymalizacyjnych, gdzie tak istotne jest precyzyjne ustalenie wartości skrajnych,
• Analiza kształtu paraboli: parametr q jest istotny przy określaniu przesunięcia w poziomie wierzchołka paraboli, na przykład, gdy chcemy przesunąć funkcję kwadratową w górę lub w dół, obliczenie q pozwala lepiej zrozumieć, jak ta zmiana wpłynie na kształt wykresu,
• Wpływ współczynników na kształt paraboli: w kontekście analizy funkcji kwadratowej, q pomaga dostrzegać, jak modyfikacje w współczynnikach a, b i c wpływają na wygląd paraboli, na przykład, zwiększenie wartości q skutkuje podniesieniem wierzchołka parabol,
• Rozwiązywanie równań kwadratowych: kiedy stajemy przed zadaniem znalezienia miejsc zerowych funkcji kwadratowej, parametr q sprawia, że łatwiej możemy zrozumieć, jak wykres układa się w przestrzeni współrzędnych, co ułatwia ustalenie punktów, w których funkcja przecina oś x.

Przykłady te ilustrują, jak wzór na q w znaczący sposób wspiera rozwiązywanie różnorodnych problemów matematycznych związanych z funkcją kwadratową.

Znaczenie q w geometrii wykresów kwadratowych

W geometrii funkcji kwadratowych parametr q odgrywa kluczową rolę w ustalaniu położenia paraboli na osi y. Dzięki jego wartości możemy precyzyjnie określić lokalizację wierzchołka paraboli, co bezpośrednio wpływa na jej kształt oraz orientację. Na przykład:

• gdy q ma wartość dodatnią, oznacza to, że wierzchołek znajduje się powyżej osi x,
• gdy q jest ujemne, wierzchołek leży poniżej tej osi.

Zrozumienie roli q znacząco usprawnia analizę graficzną funkcji kwadratowej. Umożliwia to łatwiejsze określenie punktów, w których funkcja osiąga swoje minima lub maksima, co jest istotne w wielu dziedzinach, od badań zjawisk fizycznych po projektowanie konstrukcji inżynieryjnych. Dokładne określenie kształtu oraz lokalizacji wykresu może być kluczowe w tych obszarach.

Można stwierdzić, że q stanowi istotny element w geometrii wykresów kwadratowych, mając istotny wpływ na kształt funkcji kwadratowej oraz stanowiąc podstawę do dalszej analizy i interpretacji wyników.