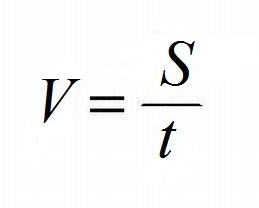Wzór na prędkość

Wzór na prędkość stanowi fundamentalne narzędzie w dziedzinie kinematyki. Pozwala on określić, jak szybko i w jakim kierunku przemieszcza się ciało w odniesieniu do ustalonego układu odniesienia. Dzięki temu można obliczać prędkość, co w praktyce oznacza analizę zmiany położenia obiektu w czasie. Używając tego wzoru, można szczegółowo badać ruch różnych obiektów, niezależnie od tego, czy poruszają się one z równą prędkością, czy też przyspieszają.

W codziennym życiu wzór na prędkość ma zastosowanie przy:

monitorowaniu ruchu pojazdów,
analizie trajektorii,
planowaniu i kontrolowaniu podróży.

W kontekście nauki i technologii odgrywa istotną rolę w badaniach nad dynamiką układów oraz ułatwia rozwiązywanie zadań dotyczących zarówno ruchu prostoliniowego, jak i krzywoliniowego.

Jaki jest podstawowy wzór na prędkość?

Podstawowy wzór na prędkość to V = s / t. W tym równaniu V oznacza średnią prędkość, s to droga przebyta przez obiekt, a t to czas, w którym ta droga została pokonana. Ten matematyczny wyraz ilustruje relację między przebywaną odległością a czasem i ma szerokie zastosowanie w obliczeniach dotyczących ruchu jednostajnego prostoliniowego.

Jednostką prędkości, zgodnie z międzynarodowym systemem jednostek (SI), jest metr na sekundę (m/s), choć w codziennym życiu częściej natrafiamy na kilometry na godzinę (km/h). Dzięki temu wzorowi, jeżeli znamy drogę oraz czas, możemy z łatwością wyliczyć, jak szybko porusza się dany obiekt.

Na przykład, jeżeli obiekt przebywa 100 metrów w ciągu 5 sekund, jego prędkość wynosi 20 m/s. Co więcej, to równanie znajduje zastosowanie w różnych dziedzinach, takich jak:

fizyka,
transport,
sporty.

To sprawia, że wzór jest niezwykle przydatny.

Kiedy stosuje się wzór v = s / t?

Wzór v = s / t jest kluczowy w opisie ruchu jednostajnego prostoliniowego, gdzie prędkość pozostaje niezmienna w czasie. Dzięki niemu możemy łatwo obliczyć średnią prędkość, dzieląc całkowitą drogę (s) przez czas (t) ruchu. Warto jednak zauważyć, że w sytuacjach, w których prędkość ulega zmianie, ten wzór dostarcza jedynie ogólnej wartości, nie uwzględniając chwilowych wahań prędkości. Mimo tego, stanowi on podstawowe narzędzie w fizyce i znajduje wiele praktycznych zastosowań, na przykład przy analizie ruchu:

samochodów,
rowerów,
innych obiektów poruszających się po prostych trasach.

Jak jednostka prędkości jest definiowana i przeliczana?

Jednostką prędkości w układzie SI jest metr na sekundę (m/s), co oznacza, że przemieszczenie danego obiektu o jeden metr zajmuje mu dokładnie jedną sekundę. W życiu codziennym często spotykamy się z prędkością wyrażaną w kilometrach na godzinę (km/h), co jest bardziej intuicyjne w kontekście podróży.

Aby przeliczyć prędkość z m/s na km/h, wystarczy:

pomnożyć przez 3,6,
w przeciwnym kierunku podzielić przez tę wartość.

To dlatego, że 1 m/s jest równy 3,6 km/h. Znajomość tych jednostek oraz umiejętność przeprowadzania konwersji ma ogromne znaczenie. To podstawowy aspekt przy rozwiązywaniu zagadnień dotyczących ruchu. Co więcej, ta wiedza przydaje się w praktyce, na przykład podczas pomiaru prędkości pojazdów lub analizowania danych z różnorodnych urządzeń pomiarowych.

Przykład przeliczenia m/s na km/h

Aby przeliczyć prędkość z metrów na sekundę (m/s) na kilometry na godzinę (km/h), wystarczy pomnożyć wartość w m/s przez 3,6. Na przykład, jeśli mamy prędkość 10 m/s, to przelicza się to na 36 km/h, ponieważ 10 razy 3,6 równa się 36. Taki sposób konwersji jednostek prędkości jest powszechnie stosowany zarówno w nauce, jak i w codziennych sytuacjach, na przykład przy pomiarze prędkości samochodów.

Aby przekonwertować km/h na m/s, wystarczy podzielić wartość przez 3,6. Tego rodzaju przeliczenia znacząco ułatwiają porównywanie wyników, co sprawia, że łatwiej jest zrozumieć dane przedstawione w różnych jednostkach miary.

Jak obliczyć prędkość w ruchu jednostajnym prostoliniowym?

Ruch jednostajny prostoliniowy charakteryzuje się poruszaniem ciała w linii prostej z niezmienną prędkością. Aby obliczyć tę prędkość, możemy skorzystać ze wzoru: V = s / t. W nim V oznacza prędkość, s to droga, jaką przebyło ciało, a t to czas tego ruchu.

W przypadku ruchu jednostajnego prędkość pozostaje stała, zarówno w kontekście średniej, jak i chwilowej. Jej wartość i kierunek nie ulegają zmianom, co sprawia, że wzór na prędkość jest niezwykle użyteczny. Umożliwia on szybkie i dokładne określenie, z jaką szybkością dane ciało się porusza. To szczególnie przydaje się w analizach ruchu oraz w rozwiązywaniu zadań z fizyki.

Dla uzyskania wiarygodnych wyników, kluczowe jest precyzyjne zmierzenie zarówno odległości, jak i czasu. Wzór V = s / t stanowi podstawowe narzędzie do określania prędkości w tego typu ruchu.

Jak wygląda wzór na prędkość w ruchu jednostajnie przyspieszonym prostoliniowym?

W ruchu prostoliniowym z jednostajnym przyspieszeniem prędkość obiektu zmienia się liniowo w miarę upływu czasu. To zjawisko wynika z ciągłego przyspieszenia. Kluczowy wzór opisujący tę zależność to: V = v0 + a·t. W tym równaniu:

V reprezentuje prędkość w danym momencie,
v0 oznacza prędkość początkową,
a to przyspieszenie,
t to czas trwania ruchu.

Dzięki temu równaniu możemy precyzyjnie obliczyć prędkość na każdym etapie ruchu, uwzględniając zmiany prędkości związane z przyspieszeniem. Jest to niezwykle istotne w analizie różnych zjawisk związanych z ruchem, takich jak:

swobodne spadanie,
proces hamowania.

Właściwe zrozumienie tego wzoru pozwala na dokładne określenie, z jaką prędkością porusza się ciało w dowolnym momencie jego ruchu jednostajnie przyspieszonego.

Jak uwzględnić przyspieszenie przy obliczaniu prędkości?

Przy obliczaniu prędkości w ruchu jednostajnie przyspieszonym prostoliniowym posługujemy się wzorem: V = v0 + a·t. Tutaj v0 oznacza prędkość początkową, ’a’ to stałe przyspieszenie, a ’t’ to czas trwania ruchu. Przyspieszenie informuje nas, w jakim tempie zmienia się prędkość w danym okresie.

Ten wzór umożliwia wyznaczenie prędkości chwilowej w dowolnym momencie ruchu. Z kolei klasyczny wzór dla ruchu jednostajnego, czyli v = s / t, nie uwzględnia dynamiki zmiany prędkości. Dlatego tak istotne staje się uwzględnienie przyspieszenia w analizie ruchów, które nie są stałe. Dzięki temu możemy dokładniej określić, jak prędkość zmienia się w czasie.

Czym różni się prędkość chwilowa od prędkości średniej?

Średnia prędkość to wskaźnik, który ilustruje, jak długo obiekt przemieszcza się w stosunku do pokonanej odległości. Oblicza się ją, dzieląc całkowity dystans przez czas, w jakim ten dystans został przemierzony. Warto jednak pamiętać, że jest to średnia, która nie uwzględnia ewentualnych zmian prędkości ani kierunku ruchu.

Z kolei prędkość chwilowa odzwierciedla tempa ruchu w danym momencie. Można ją postrzegać jako wartość graniczną średniej prędkości, obliczaną w bardzo krótkim okresie. W kontekście ruchu zmiennego prędkość chwilowa jest pochodną położenia względem czasu, co pozwala na bardziej szczegółowe określenie, jak szybko porusza się obiekt w danym punkcie czasowym.

Jak wyznaczać prędkość chwilową matematycznie?

Prędkość chwilowa jest obliczana jako pochodna funkcji położenia w odniesieniu do czasu. Możemy zapisać to w formie wzoru: v(t) = dx(t)/dt. W tym równaniu x(t) oznacza położenie obiektu w danym momencie t, a dx(t)/dt reprezentuje granicę ilorazu zmiany położenia względem zmiany czasu w miarę jak ten czas zmierza w kierunku zera.

Metoda ta, rozwinięta w ramach rachunku różniczkowego, pozwala na precyzyjne określenie prędkości w dowolnym momencie ruchu. Jest szczególnie użyteczna w sytuacjach, gdy prędkość nie pozostaje stała. Wykorzystując pochodne, jesteśmy w stanie uwzględnić zmieniające się tempo przemieszczenia, co stanowi kluczową różnicę między prędkością chwilową a średnią.

Jak kierunek i trajektoria wpływają na wartość i wektor prędkości?

Prędkość to wektor, który uwzględnia zarówno kierunek, jak i ścieżkę ruchu. Wskazuje, w którą stronę przemieszcza się obiekt, a tor ruchu określa trasę, po której się porusza. Wektor prędkości łączy ze sobą wartość prędkości oraz kierunek i zwrot.

W przypadku prostoliniowego ruchu kierunek pozostaje stały, co oznacza, że wektor prędkości nie zmienia swojego kierunku. Natomiast gdy mówimy o ruchu po krzywej lub okręgu, ścieżka ulega zmianie, co powoduje nieustanną zmianę kierunku wektora prędkości, nawet jeśli jego wartość pozostaje taka sama.

Dla pełnego zrozumienia ruchu należy brać pod uwagę nie tylko wartość prędkości, ale również jej kierunek oraz trajektorię.

Jak obliczać prędkość w praktycznych sytuacjach codziennych?

Obliczanie prędkości w życiu codziennym opiera się na prostym wzorze: V = s / t. W tym równaniu „s” reprezentuje odległość, którą pokonuje obiekt, a „t” to czas potrzebny na to przemieszczenie. Na przykład, gdy ktoś przejedzie 60 kilometrów w ciągu 2 godzin, jego prędkość wynosi 30 km/h. Umiejętność obliczania prędkości jest niezwykle przydatna podczas planowania podróży oraz szacowania czasu potrzebnego na dojazd.

W praktyce pomiar prędkości najczęściej przeprowadza się za pomocą radarów. Te zaawansowane urządzenia umożliwiają efektywne i dokładne monitorowanie ruchu pojazdów na drogach. Dzięki nim można:

sprawdzać, czy kierowcy przestrzegają ograniczeń prędkości,
wpływać na bezpieczeństwo użytkowników dróg,
poprawiać efektywność jazdy.

Obliczanie prędkości ma także zastosowanie w ocenie tempa poruszania się pieszych, rowerzystów oraz różnych środków transportowych. Posiadanie tej wiedzy ułatwia:

zarządzanie czasem i przestrzenią,
analizę efektywności ruchu.

Dlatego umiejętność obliczania prędkości na podstawie odległości i czasu jest cenną kompetencją, która przydaje się w wielu codziennych sytuacjach.

Obliczanie prędkości na podstawie przebytej drogi i czasu

Obliczenie prędkości wymaga znajomości zarówno odległości, jak i czasu, w którym została pokonana. Umożliwia to prosty wzór: V = s / t. W tym równaniu prędkość (V) stanowi stosunek przebytej drogi do czasu.

Ta technika znajduje zastosowanie w wielu dziedzinach życia, takich jak:

motoryzacja,
sport,
planowanie podróży.

Jej popularność wynika z prostoty i precyzji. Ważne jest jednak, aby odległość i czas były wyrażone w tych samych jednostkach, na przykład metrach oraz sekundach. Tylko wtedy otrzymana prędkość będzie poprawna i użyteczna.

Dlaczego pomiary radarowe są używane do monitorowania prędkości?

Pomiary radarowe to niezwykle skuteczne narzędzie do ścisłego nadzorowania prędkości. Dzięki nim możliwe jest szybkie oraz precyzyjne określenie prędkości obiektów w ruchu. Technologia ta bazuje na falach elektromagnetycznych i zjawisku Dopplera, co umożliwia uzyskiwanie dokładnych rezultatów, nawet w trudnych warunkach drogowych.

Takie systemy przyczyniają się do efektywnej egzekucji ograniczeń prędkości, co znacząco redukuje ryzyko wypadków oraz podnosi bezpieczeństwo na naszych drogach. Co więcej, radar pozwala na bieżące monitorowanie ruchu pojazdów, co znacznie ułatwia analizę zarówno natężenia, jak i dynamiki ruchu.

skuteczność w nadzorowaniu prędkości,
szybkie i precyzyjne określenie prędkości obiektów,
dokładne rezultaty w trudnych warunkach,
redukcja ryzyka wypadków,
poprawa bezpieczeństwa na drogach.

Jakie są zastosowania wzoru na prędkość w nauce i technologii?

Wzór na prędkość odgrywa fundamentalną rolę w nauce oraz technologii. Umożliwia on szczegółową analizę ruchu obiektów w mechanice klasycznej, co pozwala na dokładne określenie trajektorii oraz obliczenie energii kinetycznej, niezbędnych w takich dziedzinach, jak dynamika czy inżynieria.

Na przykład w astronomii ten wzór jest używany do określania prędkości ucieczki, czyli minimalnej prędkości potrzebnej do wydostania się z grawitacyjnego przyciągania ciał niebieskich. Warto zauważyć, że istnieje różnorodność prędkości, takich jak:

prędkość liniowa,
prędkość kątowa,
prędkość obrotowa.
prędkość orbitalna,
prędkość dźwięku.

Te różnice mają istotny wpływ na projektowanie wielu maszyn i urządzeń.

Dodatkowo, wzór na prędkość znajduje zastosowanie w technologii pomiarowej. Przykładowo, pozwala na monitorowanie maksymalnej prędkości pojazdów, co ma ogromne znaczenie w każdym aspekcie transportu. Dzięki temu, wzór na prędkość stanowi nie tylko teoretyczną podstawę, ale także praktyczny fundament dla licznych dziedzin naukowych i technicznych.

Prędkość liniowa, kątowa i obrotowa – wyjaśnienie różnic

Prędkość liniowa odnosi się do tempa, w jakim ciało porusza się wzdłuż okręgu. Można ją obliczyć, mnożąc prędkość kątową przez promień okręgu. Prędkość kątowa określa, jak szybko obiekt obraca się wokół swojej osi i jest wyrażana w radianach na sekundę. Istotnym pojęciem jest również prędkość obrotowa, która opisuje liczbę pełnych obrotów wykonanych przez ciało w określonym czasie, na przykład w obrotach na minutę.

Zrozumienie różnic między tymi pojęciami jest istotne, zwłaszcza gdy analizujemy ruch ciał poruszających się po okręgu. Oto kluczowe różnice:

prędkość liniowa koncentruje się na przesunięciu punktu po łuku,
prędkość kątowa wskazuje, jak szybko zmienia się kąt,
prędkość obrotowa to miara liczby obrotów w danym czasie.

Chociaż te trzy prędkości są wzajemnie powiązane, każda z nich opisuje inny aspekt ruchu obrotowego, co czyni je niezwykle użytecznymi w fizyce.

Jakie są przykłady prędkości szczególnych: dźwięku, światła, ucieczki?

Dźwięk w powietrzu porusza się z prędkością około 343 m/s przy standardowych warunkach,

światło w próżni osiąga imponującą prędkość 299 792 458 m/s, co czyni tę wartość jedną z kluczowych stałych w naukach przyrodniczych.

Jeśli chodzi o ucieczkę z Ziemi, potrzebujemy osiągnąć prędkość wynoszącą około 11,2 km/s, aby w ogóle móc opuścić nasze grawitacyjne pole.

Te różnorodne prędkości znajdują zastosowanie w wielu dziedzinach, takich jak:

fizyka,
astronomia,
nowoczesna technologia.

Jak wzór na prędkość pomaga w analizie ruchu i wyznaczaniu efektywności?

Wzór na prędkość odgrywa kluczową rolę w badaniu ruchu, gdyż umożliwia zrozumienie zarówno tempa, jak i kierunku poruszania się obiektów. Obliczanie prędkości średniej oraz chwilowej pozwala na precyzyjne analizowanie dynamiki ruchu, co ma znaczenie w wielu dziedzinach, takich jak:

transport,
sport,
analiza danych.

Porównując te wartości, można zauważyć istotne zmiany w ruchu, co sprzyja ulepszaniu procesów i osiąganiu lepszych wyników. Dodatkowo, prędkość stanowi fundament obliczeń energii kinetycznej, co przekłada się na możliwość oceny wykonanej pracy przez ciało oraz jego zdolności do realizacji konkretnych zadań.

W ten sposób wzór na prędkość zyskuje nie tylko status narzędzia matematycznego, lecz także staje się praktycznym wskaźnikiem efektywności oraz jakości ruchu w rozmaitych zastosowaniach.

Z jakimi pojęciami fizycznymi powiązana jest prędkość?

Prędkość jest ściśle związana z fundamentalnymi koncepcjami fizycznymi. Wśród nich można wymienić:

przemieszczenie – wektor, który ilustruje, w jaki sposób zmienia się położenie obiektu,
droga – całkowita długość przebytej trasy, będąca niezbędnym składnikiem przy wyliczaniu prędkości średniej,
czas – okres, w którym dany ruch ma miejsce,
układ odniesienia – umożliwia zdefiniowanie prędkości z perspektywy obserwatora,
energia kinetyczna – zależy od masy oraz kwadratu prędkości obiektu.

Przemieszczenie jest niezwykle ważnym elementem w obliczeniach prędkości wektorowej. Natomiast droga odnosi się do całkowitej długości przebytej trasy, co jest niezbędne do wyliczania prędkości średniej.

Układ odniesienia jest kluczowy w różnych kontekstach, umożliwiając zdefiniowanie prędkości z perspektywy obserwatora. Dodatkowo, energia kinetyczna obiektu, która zależy od jego masy oraz kwadratu prędkości, sprawia, że prędkość staje się kluczowym aspektem dynamiki ruchu i zdolności obiektu do wykonywania pracy.

Prędkość łączy się z istotnymi elementami fizyki ruchu, będąc nieodłącznym składnikiem tych rozważań.

Przemieszczenie, czas, dystans, układ odniesienia i energia kinetyczna

Przemieszczenie to wektorowa zmiana położenia obiektu, która wskazuje zarówno kierunek, jak i wartość przesunięcia pomiędzy dwoma punktami. Warto zaznaczyć, że dystans różni się od przemieszczenia – to wartość skalarna, która oznacza całkowitą długość trasy, jaką obiekt przebył, niezależnie od kierunku, w którym się poruszał.

Czas jest kluczowym czynnikiem, który pozwala nam zmierzyć, jak długo trwa ruch. Dzięki niemu możemy obliczać prędkość. Z kolei układ odniesienia to punkt lub system, w którym obserwujemy ruch ciała i dokonujemy jego pomiaru.

Energia kinetyczna, która jest związana z ruchem obiektów, obliczana jest przy użyciu wzoru: Ek = ½ m v². W tym równaniu m oznacza masę, a v prędkość danego obiektu.

Poznanie tych pojęć pozwala na dokładniejszą analizę ruchu oraz na obliczenie jego parametrów, takich jak:

prędkość,
kierunek,
energia związana z ruchem.