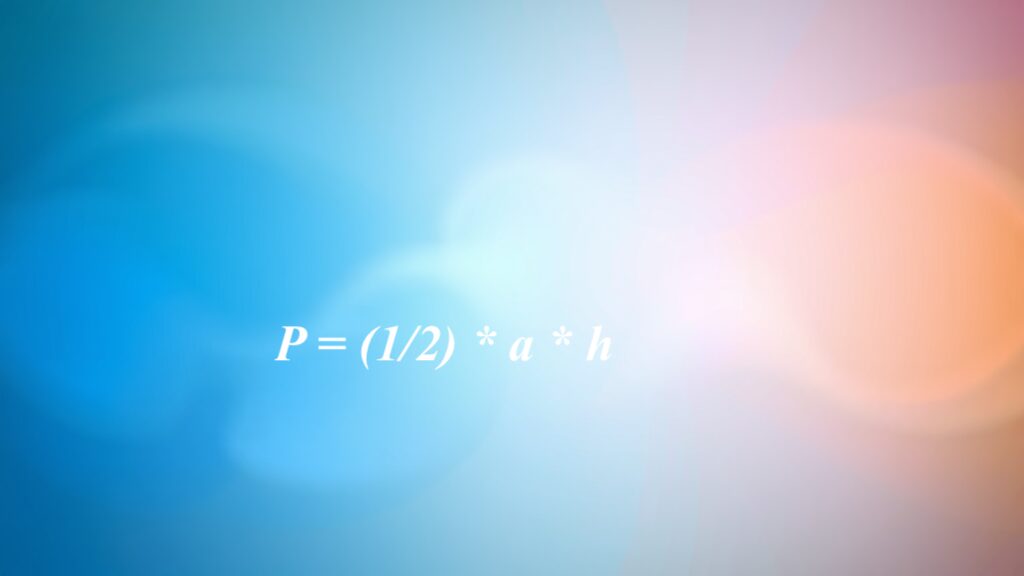Pole trójkąta to powierzchnia, którą zajmuje ten kształt w danej przestrzeni. Możemy je wyliczyć na różne sposoby, w zależności od posiadanych danych. Na przykład, jeśli znamy długości boków, wysokość lub miary kątów, każdy z tych parametrów pozwala zastosować odpowiedni wzór. Do obliczeń można także wykorzystać informacje o okręgach wpisanych lub opisanych na trójkącie. Znajomość tych formuł nie tylko ułatwia obliczenia, ale także pozwala lepiej zrozumieć właściwości trójkąta oraz jego praktyczne zastosowania.
Jak obliczyć pole trójkąta?
Pole trójkąta jest obliczane za pomocą prostego wzoru: pole = (podstawa × wysokość) / 2. Jest to tradycyjna metoda, która opiera się na długości podstawy oraz wysokości, która jest do niej prostopadła. Warto jednak wiedzieć, że istnieje wiele różnych sposobów na wyznaczenie pola trójkąta, a ich zastosowanie zależy od danych, którymi dysponujemy.
Na przykład, gdy mamy długości dwóch boków i kąt, który je łączy, możemy skorzystać z wzoru, który wykorzystuje funkcję sinus. W takim przypadku pole obliczamy w następujący sposób: pole = 0,5 × bok₁ × bok₂ × sin(kąt).
Jeśli dysponujemy długościami wszystkich trzech boków, najlepszym rozwiązaniem może być wzór Herona. Zaczynamy od obliczenia połowy obwodu, czyli s = (a+b+c)/2, a następnie korzystamy z formuły: √[s(s-a)(s-b)(s-c)], aby otrzymać pole.
Ponadto, wzory na pole trójkąta mogą również uwzględniać promień okręgu opisanego i wpisanego, co daje nam dodatkowe możliwości w obliczeniach. Wybór odpowiedniej metody zależy od dostępnych informacji:
- długości boków,
- kąty,
- wysokości,
- promienie okręgów.
Wszystkie te podejścia są ze sobą powiązane i stanowią podstawę precyzyjnych obliczeń geometrycznych, pozwalając na rozwiązanie różnorodnych problemów.
Wzór na pole trójkąta za pomocą podstawy i wysokości
Podstawowy wzór na obliczanie pola trójkąta jest niezwykle prosty do zapamiętania. Mówiąc konkretnie, pole można wyliczyć za pomocą równania P = (a * h) / 2, gdzie „a” to długość podstawy, a „h” wysokość, która jest prostopadła do tej podstawy. Wysokość jest segmentem łączącym wierzchołek trójkąta z przeciwległym bokiem, tworząc przy tym kąt prosty.
Aby uzyskać pole trójkąta, wystarczy wziąć połowę iloczynu długości podstawy z wysokością. Ten prosty wzór jest powszechnie stosowany nie tylko ze względu na łatwość zapamiętania, ale także jego uniwersalność; można go stosować do różnych rodzajów trójkątów, o ile znamy długości podstawy i wysokości.
Wzór na pole trójkąta prostokątnego
Pole trójkąta prostokątnego można łatwo obliczyć, korzystając z prostej formuły: P = (a * b) / 2. W tym równaniu a i b oznaczają długości przyprostokątnych, które to boki sąsiadują ze sobą pod kątem prostym, wynoszącym 90 stopni.
Ciekawostką jest, że wysokość takiego trójkąta odpowiada długości jednej z przyprostokątnych. Oznacza to, że mnożąc długości tych boków, otrzymujemy podwójną wartość pola. Dzięki temu wzór na pole trójkąta prostokątnego stanowi skuteczny i szybki sposób na wyliczenie jego powierzchni.
| Metoda | Wzór | Wymagane dane | Uwagi |
|---|---|---|---|
| Podstawa i wysokość | P = (a × h) / 2 | długość podstawy (a), wysokość (h) prostopadła do podstawy | Metoda podstawowa, uniwersalna dla różnych trójkątów |
| Trójkąt prostokątny | P = (a × b) / 2 | długości przyprostokątnych (a, b) | Wysokość równa jednemu z boków; szybkie obliczenie pola |
| Trygonometryczna (dwa boki i kąt między nimi) | P = 0,5 × a × b × sin(γ) | długości dwóch boków (a, b), kąt między nimi (γ) | Nie wymaga wysokości; wykorzystuje funkcję sinus |
| Wzór Herona | P = √[p(p – a)(p – b)(p – c)] gdzie p = (a + b + c) / 2 | długości trzech boków (a, b, c) | Wylicza pole bez znajomości wysokości lub kątów |
| Z wykorzystaniem promienia okręgu opisanego (R) | P = (a × b × c) / (4 × R) | długości boków (a, b, c), promień okręgu opisanego (R) | Łączy geometrię okręgów i trójkąta |
| Z wykorzystaniem promienia okręgu wpisanego (r) | P = r × p gdzie p = (a + b + c) / 2 | promień okręgu wpisanego (r), połowa obwodu (p) | Proste obliczenie pola z promienia i półobwodu |
Kiedy stosować poszczególne wzory na pole trójkąta?
Wzór na obliczenie pola trójkąta zmienia się w zależności od dostępnych informacji geometrycznych. Możemy skorzystać z następujących metod:
- gdy dysponujemy długością podstawy oraz odpowiadającą jej wysokością, możemy użyć równania: P = (a * h) / 2,
- w przypadku trójkąta prostokątnego, jeśli znamy długości obu przyprostokątnych, pole jest równe połowie ich iloczynu,
- gdy znamy dwa boki i kąt między nimi, pole można obliczyć za pomocą wzoru: P = (1/2) * a * b * sin(γ),
- jeśli dysponujemy długościami wszystkich trzech boków, możemy skorzystać z wzoru Herona, który opiera się na połowie obwodu oraz długościach boków,
- wzory z użyciem promienia okręgu wpisanego czy opisanego mogą być przydatne, gdy mamy promień oraz odpowiednie długości boków lub obwód trójkąta.
Dzięki tym różnorodnym wzorom jesteśmy w stanie dokładnie obliczyć pole trójkąta, stosując adekwatną metodę w zależności od dostępnych danych.
Jak wysokość, podstawa i kąty wpływają na pole trójkąta?
Aby obliczyć pole trójkąta, najprostszym sposobem jest:
- pomnożenie długości podstawy przez odpowiadającą jej wysokość,
- podzielenie wyniku przez dwa.
Wysokość, będąca odcinkiem prostopadłym, prowadzi z wierzchołka do podstawy trójkąta. Im wyższa wysokość przy stałej długości podstawy, tym większe pole uzyskujemy.
Kąty trójkąta również odgrywają kluczową rolę w obliczeniach:
- korzystanie z wzoru, który uwzględnia sinusy,
- możliwość określenia pola jako połowy iloczynu długości dwóch boków oraz sinusa kąta między nimi.
Dzięki tej właściwości znajomość kątów pozwala nam na wyliczenie pola trójkąta bez konieczności ustalania jego wysokości. Zmiana miary kąta wpływa na wartość sinusa, co z kolei oddziałuje na obliczane pole, pod warunkiem, że długości boków pozostają niezmienne.
Wszystkie te czynniki – wysokość, podstawa oraz miary kątów – pozwalają na tworzenie różnych wzorów do obliczania pola trójkąta, co daje nam możliwość dopasowania metody do posiadanych informacji:
- wysokość i podstawa dostarczają klasycznej definicji pola,
- kąty oraz długości boków otwierają nowe perspektywy w obliczeniach trygonometrycznych.
Co to jest połowa obwodu trójkąta i jakie ma znaczenie przy obliczeniach?
Połowa obwodu trójkąta, znana jako p, to istotna wartość, która stanowi połowę sumy długości wszystkich trzech boków tego figury:
p = (a + b + c) / 2. To kluczowy koncept w obliczeniach, zwłaszcza w kontekście wzoru Herona, który umożliwia nam wyliczenie pola, posiadając jedynie długości boków, bez konieczności znajomości wysokości czy kątów.
Wzór Herona jest niezwykle przydatny, ponieważ pole trójkąta można określić bez dodatkowych informacji. Co więcej, połowa obwodu odgrywa rolę w formule na pole trójkąta, wykorzystując promień okręgu wpisanego. W tym przypadku pole jest równe iloczynowi promienia okręgu wpisanego oraz wartości p.
Dzięki temu pojęcie połowy obwodu staje się użytecznym narzędziem w geometrii trójkątów, ułatwiając skuteczne obliczenia w różnych sytuacjach.
Jak promień okręgu wpisanego i opisanego wpływa na pole trójkąta?
Promień okręgu opisanego (R) oraz promień okręgu wpisanego (r) odgrywają istotną rolę w obliczeniach pola trójkąta, ponieważ umożliwiają wykorzystanie różnych formuł.
Można obliczyć pole trójkąta, posługując się promieniem okręgu opisanego za pomocą wzoru:
P = (a * b * c) / (4 * R).
W tej formule a, b i c oznaczają długości boków trójkąta. Dzięki temu podejściu możemy powiązać długości boków z promieniem okręgu opisanego, co pozwala obliczyć pole bez konieczności ustalania wysokości.
Natomiast promień okręgu wpisanego (r) wykorzystuje półobwód trójkąta (p) zgodnie z równaniem:
P = r * p,
gdzie p = (a + b + c) / 2.
Ta formuła opiera się na właściwościach okręgu wpisanego i pozwala na szybkie obliczenie pola, dysponując jedynie promieniem i półobwodem.
W ten sposób oba promienie, R i r, stają się kluczowymi składnikami łączącymi geometrię okręgów z geometrią trójkąta, co ułatwia obliczenia pól trójkątów w różnych sytuacjach.
Jak zastosować trygonometrię do obliczania pola trójkąta?
Trygonometria umożliwia obliczenie pola trójkąta, gdy mamy do dyspozycji długości dwóch boków oraz kąt, który znajduje się między nimi. Wykorzystujemy do tego wzór P = (1/2) * a * b * sin(γ), gdzie a i b oznaczają długości boków, a γ to kąt pomiędzy nimi.
Sinus kąta γ jest przydatny przy określaniu wysokości trójkąta w odniesieniu do jego podstawy. Co istotne, nie ma potrzeby bezpośredniego mierzenia tej wysokości. Takie podejście sprawdza się doskonale, zwłaszcza w sytuacjach, gdy pomiar może być trudny lub niemożliwy do zrealizowania.
Dodatkowo, zasady sinusów oraz cosinusów wspierają nasze działania, pozwalając na odnalezienie brakujących długości lub kątów, które są niezbędne do stosowania wcześniej wspomnianego wzoru. Dzięki tym metodom trygonometria staje się niezwykle użytecznym narzędziem do obliczania pola trójkątów o przeróżnych kształtach, zapewniając dokładne wyniki, nawet w sytuacjach, gdzie nie dysponujemy wszystkimi wymiarami.
Jakie są najczęstsze błędy podczas obliczania pola trójkąta?
Najczęściej popełniane błędy przy obliczaniu pola trójkąta wynikają głównie z:
- mylenia podstawy z innymi bokami, co skutkuje niewłaściwym ustaleniem jej długości,
- bieżnych problemów z błędnym określeniem wysokości, złe pomiary lub wybór niewłaściwego punktu odniesienia mogą znacząco utrudnić obliczenia,
- pomyłek podczas stosowania wzorów, szczególnie tych z funkcjami trygonometrycznymi,
- niepoprawnego podstawienia kątów w takich wzorach, co prowadzi do nietrafnych wyników,
- błędnych obliczeń semiperimetru, czyli połowy obwodu w ramach wzoru Herona,
- mylenia promieni okręgu wpisanego i opisanego.
Kluczowe jest, aby stosować jednolite jednostki miar, ponieważ ich niespójność może wprowadzać zamieszanie oraz prowadzić do fałszywych wyników. Dogłębne zrozumienie geometrii trójkąta oraz staranne sprawdzanie danych to skuteczne metody na zminimalizowanie tych typowych błędów.
Jak obliczyć pole trójkąta na podstawie ćwiczeń i przykładów?
Obliczanie powierzchni trójkąta wiąże się z praktycznym zastosowaniem różnych wzorów i technik. Na początku nauki korzystamy z podstawowego wzoru, który uwzględnia długość podstawy i wysokość. W przypadku trójkąta prostokątnego proces ten jest szczególnie prosty, ponieważ możemy wykorzystać dwie przyprostokątne jako podstawę oraz wysokość.
Kolejnym przydatnym narzędziem jest wzór Herona, który pozwala na wyznaczenie pól, gdy znamy długości wszystkich trzech boków. Takie ćwiczenia pomagają zrozumieć, jak obliczać półobwód i wartości pod pierwiastkiem. Innym sposobem są zadania oparte na wzorach z kątami i sinusami, które pozwalają obliczyć pole, gdy dysponujemy miarami kątów oraz długościami dwóch boków.
Warto również zwrócić uwagę na zadania związane z promieniami okręgów wpisanego lub opisanego, co wymaga zrozumienia ich wpływu na pole trójkąta. Często można spotkać animacje oraz wizualizacje, które znacząco ułatwiają uchwycenie związku między podstawą, wysokością, kątami i obliczaniem powierzchni.
Regularne ćwiczenie z różnorodnymi typami trójkątów pozwala nie tylko na lepszy dobór wzorów, ale także na precyzyjniejsze wykonywanie obliczeń dotyczących pól.
Dlaczego pole trójkąta jest istotne w matematyce i geometrii?
Pole trójkąta to istotne pojęcie w świecie matematyki i geometrii, które pozwala na precyzyjne określenie powierzchni tej kluczowej figury płaskiej. Jego zrozumienie jest niezbędne do rozwiązywania różnych problemów geometrycznych. Co więcej, ma także wiele praktycznych zastosowań w takich dziedzinach jak:
- architektura,
- inżynieria,
- fizyka,
- grafika komputerowa.
To, co wyróżnia pole trójkąta, to jego rola w kształtowaniu wzorów dotyczących bardziej złożonych figur. Stanowi ono narzędzie, które umożliwia analizę kształtów oraz odwzorowanie zależności przestrzennych. Dzięki swojej uniwersalności, to pojęcie jest jednym z podstawowych elementów nauk ścisłych, dając możliwość modelowania i projektowania obiektów w rozmaitych obszarach.
Jak wizualizować obliczanie pola trójkąta za pomocą animacji?
Animacja skutecznie ułatwia zrozumienie, jak obliczyć pole trójkąta. Dzięki niej możemy zobaczyć cały proces krok po kroku, co czyni naukę bardziej intuicyjną. Ilustruje, jak prawidłowo znaleźć wysokość spadającą na podstawę, a także jak obliczyć iloczyn długości podstawy i wysokości.
Co więcej, animacja pokazuje różnice między trójkątami o różnych kształtach i kątach, co znacznie upraszcza zgłębianie geometrii. Za pomocą dynamicznych elementów, takich jak:
- ruszające się boki,
- zmieniające się kąty,
- możliwość wizualizacji zmian,
- obliczanie pola w kontekście kształtu,
- intuicyjna nauka wzorów.
Taki sposób prezentacji sprawia, że przyswajanie wzorów i zasad związanych z polem trójkąta staje się znacznie łatwiejsze i bardziej zrozumiałe.