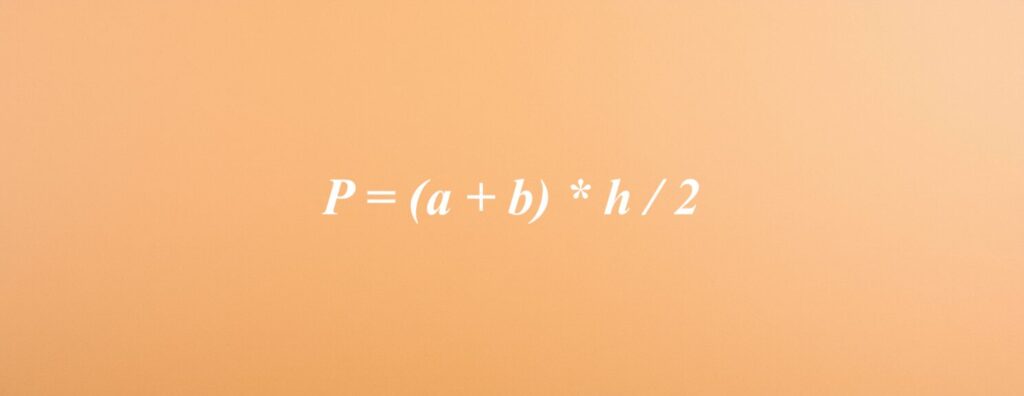Wzór na pole trapezu równoramiennego

Trapez równoramienny to fascynująca figura geometryczna, którą zaliczamy do czworokątów. Cechuje się on posiadaniem dwóch równoległych podstaw oraz ramion o tej samej długości, co nadaje mu harmonijny wygląd. Najbardziej charakterystyczną cechą tego trapezu jest jego symetria, wyrażająca się poprzez oś symetrii biegnącą przez środkowe punkty obu podstaw. Dzięki temu kąty przylegające do podstaw są równe, a długości jego przekątnych również się ze sobą zgadzają.

Definicja trapezu obejmuje czworokąty, które mają przynajmniej jedną parę boków równoległych, jednak trapez równoramienny jest specyficznym przypadkiem, gdzie dodatkowo ramiona są równorzędne. Przykładowo, jeżeli jedna podstawa ma długość 6 cm, a druga 4 cm, ramiona również będą miały tę samą miarę. Taki układ znacznie ułatwia rozwiązywanie zadań matematycznych związanych z tego typu trapezem.

Oprócz cech geometrycznych, trapez równoramienny jest doceniany także w różnych dziedzinach, takich jak architektura czy sztuka. Jego unikalne proporcje i estetyka często inspirują projektantów do wykorzystania w różnorodnych realizacjach.

Jakie są własności trapezu równoramiennego?

Trapez równoramienny charakteryzuje się kilkoma interesującymi właściwościami geometrycznymi:

jego ramiona mają jednakową długość,
podstawy trapezu są równoległe,
kąty przy podstawach są równe,
suma kątów wewnętrznych wynosi 360 stopni,
przeciwległe kąty łączą się w 180 stopni.

Te cechy są niezbędne w rozwiązywaniu zadań geometrycznych związanych z trapezami.

Przekątne trapezu równoramiennego mają identyczną długość, co sprawia, że trapez dysponuje osią symetrii, która biegnie przez środki obu podstaw, dzieląc go na dwie równe części. Ta oś jest niezwykle przydatna w badaniach nad właściwościami geometrycznymi oraz w obliczeniach dotyczących pola i obwodu trapezu.

Znajomość tych cech trapezu równoramiennego jest kluczowa dla zrozumienia jego zastosowań w geometrii oraz w praktycznych zagadnieniach inżynieryjnych czy architektonicznych.

Podstawy i ramiona trapezu

Podstawy trapezu równoramiennego składają się z dwóch równoległych boków, z których dłuższy zazwyczaj oznaczamy literą „a”, a krótszy „b”. Długości tych trzech boków są kluczowe nie tylko w obliczeniach pola, ale również w określaniu obwodu trapezu. Ważną rolę odgrywają tu ramiona, które są oznaczane jako „c”; w tym typie trapezu mają one jednakową długość. Taki układ wpływa zarówno na symetrię całej figury, jak i na jej wysokość.

Suma długości podstaw, czyli a + b, jest niezbędna w wielu zadaniach geometrycznych związanych z obliczaniem pola. Ramiona oddziałują na właściwości trapezu, wpływając między innymi na:

kąty przy podstawach,
wysokość,
symetrię figury.

Wiele zadań dotyczących trapezów równoramiennych wymaga starannych pomiarów zarówno podstaw, jak i ramion, co znacząco upraszcza całe rozwiązywanie problemów.

Kąty przy podstawach i suma kątów

Kąty u podstaw trapezu równoramiennego odgrywają kluczową rolę w jego geometrze. W tej figurze kąty te tworzą pary równych miar, co jest efektem jej symetrycznej budowy. Oznacza to, że jeśli jeden z kątów ma wartość α, to drugi także przyjmuje tę samą miarę. Natomiast kąty przeciwległych podstaw sumują się do 180 stopni, co jest równie ważne w kontekście geometrii.

Właściwości tych kątów mają konkretne zastosowania w dziedzinie trygonometrii, umożliwiając skuteczne obliczenie wysokości oraz pola trapezu. Zrozumienie ich relacji ułatwia także analizę boków figury, co pozwala na świadome stosowanie różnych wzorów, szczególnie w skomplikowanych problemach geometrycznych związanych z trapezami.

Zrozumienie tych kątów jest niezbędne dla pojęcia symetrii trapezu oraz jego unikalnych cech. Jest to szczególnie istotne podczas rozwiązywania różnorodnych zadań. Dodatkowo, znajomość sumy miar kątów przydaje się w przewidywaniu, jak figura będzie się zachowywać w bardziej złożonych rysunkach czy obliczeniach.

Przekątne i oś symetrii

Przekątne trapezu równoramiennego łączą przeciwległe wierzchołki i mają tę samą długość, co stanowi istotny element tej figury. Długość przekątnych można obliczyć, znając rozmiary podstaw oraz ramion trapezu. Te linie odgrywają ważną rolę w wielu problemach geometrycznych, które wymagają zrozumienia relacji przestrzennych między wierzchołkami.

Oś symetrii trapezu równoramiennego przebiega przez środki podstaw, dzieląc go na dwie identyczne połowy. Kąty przy podstawach są równe, co dodatkowo podkreśla symetrię kształtu. Oś symetrii jest kluczowym elementem w szkicach pomocniczych oraz zadaniach dotyczących trapezów, ponieważ ułatwia obliczenia oraz zwiększa jasność w analizie figury.

Przekątne trapezu równoramiennego, będące równej długości przez symetrię, w połączeniu z osią symetrii, znacznie upraszczają rysowanie i analizowanie tej figury. Te cechy są nieocenione w trakcie różnych obliczeń oraz pomagają lepiej zrozumieć budowę trapezu równoramiennego.

Wzór na pole trapezu równoramiennego

Wzór na pole trapezu równoramiennego można opisać jako P = (a + b) * h / 2, gdzie a i b oznaczają długości jego podstaw, a h to wysokość. Ta zwięzła formuła sprawia, że obliczanie pola trapezu równoramiennego staje się naprawdę intuicyjne i proste.

Warto podkreślić, że elastyczność tego wzoru pozwala na jego zastosowanie w różnych kontekstach. Na przykład, kiedy posiadamy długości ramion trapezu oraz kąt przy jednej z podstaw, możemy sięgnąć po inny wzór: P = 1/2 * e^2 * sin(β), gdzie e to długość ramion, a β to wspomniany kąt.

Dzięki takim równaniom z łatwością wyliczymy pole trapezu równoramiennego, co jest niezwykle przydatne w zadaniach z geometrii. Zrozumienie wzoru na pole trapezu otwiera drzwi do szerszego pojmowania bardziej zaawansowanych konceptów geometrycznych.

Co oznaczają poszczególne elementy wzoru?

Wzór na pole trapezu równoramiennego jest wyrażony jako P = (a + b) * h / 2. Przyjrzyjmy się, co oznaczają poszczególne składniki:

a i b: to długości podstaw trapezu, które są równoległe. Ich suma, czyli a + b, odgrywa kluczową rolę przy obliczaniu powierzchni,
h: wysokość trapezu, to w rzeczywistości odległość prostopadła między jego podstawami. To bardzo istotny wymiar, ponieważ określa, jak „wysoki” jest trapez, co w efekcie wpływa na jego całkowite pole.

Obliczenia polegają na pomnożeniu sumy długości podstaw przez wysokość i podzieleniu wyniku przez dwa. To efektywnie ilustruje zasady kalkulacji pola w trapezach.

Istnieje również alternatywna forma wzoru na pole trapezu równoramiennego, która wygląda następująco: P = 1/2 * e^2 * sin(β). W tym ujęciu:

e: to długość ramion trapezu, co jest szczególnie przydatne, gdy ciężko zmierzyć długości podstaw,
β: kąt przy podstawie, którego znaczność uwzględnia funkcja sinus. Umożliwia to dokładniejsze obliczenia, biorąc pod uwagę kąt między ramionami.

Te różne elementy wzoru pozwalają na precyzyjne ustalenie pola trapezu, dostosowując się do dostępnych danych.

Kiedy stosować alternatywne wzory?

Alternatywny sposób obliczania pola trapezu równoramiennego, wyrażony jako P = 1/2 * e² * sin(β), okazuje się niezwykle przydatny w sytuacjach, gdy dysponujemy długościami ramion trapezu oraz kątem przy podstawie, ale brakuje nam informacji na temat wysokości. Dzięki temu wzorowi możemy efektywnie wykorzystać funkcje trygonometryczne do znalezienia pola. Takie podejście jest szczególnie wartościowe w zadaniach, gdzie znane są zarówno kąty, jak i długości ramion.

Stosowanie alternatywnych wzorów ma istotne znaczenie w praktyce, zwłaszcza w kontekście skomplikowanych obliczeń, które wymagają bardziej zaawansowanych metod. Eliminując konieczność ustalania wysokości trapezu, możemy z łatwością przejść do obliczeń pola. Taki sposób znacznie przyspiesza proces rozwiązywania problemów. Warto z niego korzystać zwłaszcza wtedy, gdy precyzyjne wyniki są kluczowe; dostępne dane dotyczące kątów i długości ramion w zupełności wystarczą do dalszych analiz.

Jak wyprowadzić wzór na pole trapezu równoramiennego?

Wzór na pole trapezu równoramiennego można wyprowadzić, biorąc pod uwagę długości jego podstaw, wysokość oraz symetrię. Klasyczna metoda polega na podziale trapezu na prostokąt oraz dwa trójkąty prostokątne. W przypadku trapezu równoramiennego długości obu podstaw są identyczne, a ramiona mają tę samą długość, co znacząco upraszcza nasze obliczenia.

Zacznijmy od oznaczenia długości podstaw. Przyjmijmy, że górna podstawa to a, a dolna to b, natomiast wysokość wynosi h. Aby obliczyć wysokość trapezu, możemy zastosować twierdzenie Pitagorasa. Po podziale trapezu uzyskujemy prostokąt o podstawach a i b oraz dwa trójkąty prostokątne. Wysokość tych trójkątów to h, a podstawy można obliczyć jako różnicę (b – a)/2. Następnie stosujemy wzór na pole trapezu:

Pole = (a + b) * h / 2.

Oprócz tej metody, istnieje również alternatywna, której zastosowanie jest równie skuteczne. Możemy skorzystać z funkcji trygonometrycznych, szczególnie jeśli znamy długości ramion oraz kąt przy podstawie. W takim przypadku posługujemy się wzorem:

Pole = 1/2 * (a + b) * (ramię * sin(α)),

gdzie α oznacza kąt przy podstawie. Oba podejścia bazują na unikalnych właściwościach trapezu równoramiennego, co pozwala nam uzyskać odpowiedni wzór na pole.

Wartości uzyskane w wyniku tych obliczeń są zgodne z zasadami geometrii i odgrywają kluczową rolę w rozwiązywaniu problemów związanych z trapezami w zadaniach matematycznych.

Wyprowadzenie wzoru klasycznego

Aby obliczyć powierzchnię trapezu równoramiennego, możemy skorzystać z tradycyjnych metod. Rozpoczynamy, dzieląc trapez na prostokąt oraz dwa trójkąty prostokątne.

Mamy trapez, w którym długości podstaw wynoszą a i b, a ramiona mają długość c. Zakładamy, że długości podstaw są różne, ale ramiona pozostają jednakowe. Wysokość trapezu, oznaczana symbolem h, można wyznaczyć przy pomocy twierdzenia Pitagorasa. Wzór na jej obliczenie przedstawia się następująco:

h = √(c² – ((a – b)² / 4)).

W tym równaniu ((a – b)² / 4) reprezentuje połowę różnicy długości podstaw. To ważny krok, ponieważ pozwala utworzyć trójkąty prostokątne.

Kiedy uda nam się obliczyć wysokość h, możemy przejść do obliczenia powierzchni trapezu P, używając formuły:

P = (a + b) * h / 2.

Ten wzór łączy kluczowe elementy, takie jak długości podstaw oraz wysokość. Dlatego jest on nieocenionym narzędziem w geometrii.

Zastosowanie funkcji trygonometrycznych

Funkcje trygonometryczne odgrywają kluczową rolę w geometrii, zwłaszcza w kontekście obliczania pól trapezów równoramiennych. Na przykład, możemy wykorzystać sinus kąta przy podstawie trapezu, co pozwala na alternatywne wyprowadzenie wzoru na jego pole.

Aby obliczyć pole trapezu równoramiennego, wystarczy znać długość ramienia „e” oraz kąt „β”, co umożliwia skorzystanie z następującego wzoru:

P = 1/2 * e^2 * sin(β).

To podejście jest niezwykle użyteczne, gdy nie mamy dostępu do wysokości trapezu, ale dysponujemy informacjami na temat kątów i długości ramion. Dzięki tej metodzie możliwe jest uzyskiwanie precyzyjnych wyników. W ten sposób funkcje trygonometryczne stają się nie tylko narzędziem geometrii, ale również istotnym wsparciem w zadaniach dotyczących trapezów. Co więcej, ich zastosowanie poprawia dokładność obliczeń oraz pozwala na lepsze zrozumienie zależności między kątami a bokami trapezu.

Jak obliczyć wysokość trapezu równoramiennego?

Wysokość trapezu równoramiennego to ważny element geometrii, który możemy obliczyć, korzystając z twierdzenia Pitagorasa. Oznaczana jako h, wysokość ta mierzy odległość prostopadłą między dwiema podstawami trapezu. Aby ustalić jej wartość, konieczne są długości podstaw (a i b) oraz długość ramienia (c).

Wzór na obliczenie wysokości trapezu równoramiennego wygląda następująco:

h = √(c² – ((a – b)² / 4))

W tym równaniu (a – b) / 4 odzwierciedla różnicę długości podstaw, podczas gdy c² reprezentuje kwadrat długości ramienia. Dzielimy różnicę przez 4, ponieważ wysokość jest prostopadła do podstaw, co tworzy po obu stronach trapezu dwa identyczne trójkąty prostokątne.

Obliczenie wysokości jest niezwykle istotne. Ta wartość odgrywa kluczową rolę w dalszych kalkulacjach, takich jak wyznaczanie pola trapezu równoramiennego. Dzięki podanemu wzorowi możemy szybko i sprawnie obliczyć wysokość, co znacznie ułatwia rozwiązywanie różnych problemów geometrze związanych z trapezami.

Wzór wykorzystujący twierdzenie Pitagorasa

Wzór na wysokość trapezu równoramiennego, oparty na swoistym twierdzeniu Pitagorasa, umożliwia dokładne obliczenia, nawet gdy wysokość nie jest znana. Możemy określić wysokość trapezu (h) przy użyciu następującego wzoru:

h = √(c² – ((a – b)² / 4))

W tym równaniu:

c oznacza długość ramienia trapezu,
a oraz b to długości jego podstaw.

Aby wyprowadzić ten wzór, należy najpierw skonstruować trójkąt prostokątny. Można to zrobić, opuszczając wysokość na jedną z podstaw trapezu. W takim trójkącie:

ramię ma długość c,
wysokość to h,
podstawa trójkąta odpowiada połowie różnicy długości podstaw trapezu, co zapisujemy jako (a – b)/2.

Dzięki zastosowaniu twierdzenia Pitagorasa możemy obliczyć wysokość trapezu, co jest niezbędne do dalszych obliczeń, takich jak pole czy obwód tej figury.

Wysokość a długości podstaw i ramienia

Wysokość trapezu równoramiennego odgrywa kluczową rolę w obliczeniach geometrycznych. Jej wartość ma bezpośredni wpływ na pole tej figury, co czyni ją niezwykle istotnym wymiarem. Długości podstaw, oznaczane jako a i b, a także długość ramienia, c, są niezbędne do precyzyjnego określenia wysokości.

Aby obliczyć wysokość h trapezu równoramiennego, stosuje się wzór: h = √(c² – ((a – b)² / 4)). Interesujące jest to, że różnica pomiędzy długościami podstaw (a i b) istotnie wpływa na wysokość. Zasada jest prosta: im większa różnica, tym wyższa wysokość. To ma kluczowe znaczenie podczas obliczania pola trapezu, ponieważ wysokość zawsze jest prostopadła do podstaw.

Długości ramion trapezu, oznaczane jako c, również nie są bez znaczenia. Przyczyniają się do precyzyjnego obliczenia wysokości oraz wpływają na stabilność całej figury. Zrozumienie, jak długości podstaw i ramion trapezu współdziałają, jest fundamentem nie tylko w geometrii, ale także przy rozwiązywaniu praktycznych zadań związanych z trapezami równoramiennymi.

Jak obliczyć pole trapezu równoramiennego krok po kroku?

Aby obliczyć pole trapezu równoramiennego, warto przejść przez kilka istotnych etapów. Dzięki nim zapewnimy, że nasze wyniki będą prawidłowe.

Na samym początku ustalamy długości podstaw trapezu. Mamy górną podstawę, którą oznaczamy jako a, oraz dolną, określaną jako b. Następnie niezbędne będzie zmierzenie lub obliczenie wysokości trapezu (h). Gdy nie znamy wysokości, z pomocą przychodzi twierdzenie Pitagorasa. Wzór na wysokość opiera się na długości ramion trapezu oraz kącie, jaki tworzą podstawy.

Gdy zgromadzimy wszystkie istotne dane, przechodzimy do kolejnego kroku – zastosowania wzoru na pole trapezu równoramiennego:

P = (a + b) * h / 2.

Na przykład, jeśli górna podstawa ma 5 cm, dolna 7 cm, a wysokość wynosi 4 cm, obliczenie powierzchni trapezu wygląda następująco:

P = (5 + 7) * 4 / 2 = 24 cm².

Warto również poznać alternatywne metody obliczeń, takie jak wykorzystanie funkcji sinus, jeśli dysponujemy informacjami o kącie przy podstawie i długości ramion trapezu.

Aby lepiej zrozumieć ten proces, można posłużyć się różnorodnymi przykładami. Pamiętaj, aby upewnić się, że wszystkie jednostki są zgodne. Dobrze jest także przeprowadzić interaktywne ćwiczenia, które pomogą utrwalić wiedzę na temat obliczania pola trapezu równoramiennego.

Przykłady obliczeń z danymi liczbowymi

Przykłady obliczeń z wykorzystaniem liczb są niezwykle istotne, by lepiej zrozumieć, jak efektywnie stosować wzory do wyznaczania pola trapezu równoramiennego oraz jego wysokości. Zacznijmy od podstawowego wzoru na pole trapezu:

P = \frac{(a + b) \cdot h}{2}

W tej formule:

P to pole trapezu,
a i b reprezentują długości podstaw,
h oznacza wysokość.

Przykładowo, rozważmy trapez równoramienny z podstawami o długościach a = 8 \, \text{cm} oraz b = 4 \, \text{cm}, gdzie wysokość wynosi h = 5 \, \text{cm}. Obliczenia pola trapezu będą wyglądały następująco:

P = \frac{(8 + 4) \cdot 5}{2} = \frac{12 \cdot 5}{2} = \frac{60}{2} = 30 \, \text{cm}^2

Teraz przejdźmy do kolejnego zadania – określenia wysokości trapezu. W tym celu skorzystamy z wzoru na wysokość:

h = \sqrt{c^2 – \left(\frac{a – b}{2}\right)^2}

Przyjmijmy, że długości ramion trapezu wynoszą c = 6 \, \text{cm}, a podstawy mają długości a = 8 \, \text{cm} i b = 4 \, \text{cm}:

h = \sqrt{6^2 – \left(\frac{8 – 4}{2}\right)^2} = \sqrt{36 – \left(2\right)^2} = \sqrt{36 – 4} = \sqrt{32} \approx 5.66 \, \text{cm}

Te podane przykłady ilustrują praktyczne zastosowanie wzorów w kontekście trapezu równoramiennego, co znacznie ułatwia przyswajanie wiedzy, dzięki konkretnym wartościom liczbowym.

Ćwiczenia interaktywne z rozwiązaniami

Ćwiczenia interaktywne z rozwiązaniami stanowią znakomity sposób na naukę oraz utrwalanie wiedzy na temat trapezu równoramiennego. Pozwalają uczniom na praktyczne zastosowanie wzorów dotyczących:

pola,
wysokości,
obwodu trapezu.

Takie aktywności często obejmują ciekawe zadania, które pomagają zwiększyć pewność siebie podczas obliczeń.

Rysunki trapezów oraz różnorodne ilustracje efektownie wizualizują właściwości tej figury, takie jak:

kąty,
długości ramion.

Uczniowie mają okazję krok po kroku rozwiązywać problemy, dzięki czemu lepiej przyswajają kluczowe koncepcje oraz metody obliczeniowe. Interaktywne platformy edukacyjne proponują szeroki wachlarz formatów zadań, co sprzyja aktywnemu przyswajaniu wiedzy.

Taki sposób nauki umożliwia uczniom efektywne ćwiczenie i samodzielne weryfikowanie swoich odpowiedzi, co przyczynia się do lepszego zapamiętywania materiału oraz wzorów. Ćwiczenia te stają się szczególnie cenne przed sprawdzianami i egzaminami, gdzie znajomość trapezów oraz umiejętność ich obliczania okazuje się niezbędna.

Jak obliczyć obwód trapezu równoramiennego?

Obliczenie obwodu trapezu równoramiennego jest proste. Obwód, oznaczany jako L, to suma długości wszystkich boków trapezu. W przypadku trapezu równoramiennego mamy dwie podstawy, które są równoległe, oraz dwa ramiona o tej samej długości. Wzór na jego obliczenie jest następujący:

L = a + b + 2c

Gdzie:

a to długość jednej podstawy,
b to długość drugiej podstawy,
c to długość ramienia trapezu.

Pamiętaj, aby wszystkie długości a, b i c były wyrażone w tych samych jednostkach. Dzięki temu, że ramiona trapezu równoramiennego są identyczne, obliczenia stają się prostsze.

Obwód odgrywa istotną rolę w geometrii. Jest niezbędny do wielu dalszych obliczeń, na przykład do wyznaczania pola trapezu. Może być również użyteczny w zadaniach geometrycznych wymagających znać całkowity obwód figury.

Aby lepiej przyswoić tę umiejętność, warto spróbować obliczeń na konkretnych przykładach liczbowych. Ułatwi to zrozumienie i pozwoli utrwalić poznane zasady.

Wzór na obwód i przypadki szczególne

Wzór na obwód trapezu równoramiennego można zapisać jako \( L = a + b + 2c \). Tutaj „a” i „b” wskazują długości podstaw, podczas gdy „c” przedstawia długość ramion. Dzięki temu równaniu szybko obliczamy całkowity obwód figury, co jest szczególnie przydatne w zadaniach z geometrii.

W przypadku trapezu prostokątnego, wzór na obwód pozostaje taki sam, lecz obliczenia mogą być prostsze, ponieważ jedno z ramion jest prostopadłe do podstaw. Zrozumienie wzoru na obwód trapezu znacząco ułatwia rozwiązywanie różnorodnych problemów geometrycznych, co jest istotną umiejętnością w dziedzinie matematyki.

Gdy znamy długości podstaw i ramion, obliczenie obwodu sprowadza się do prostego dodawania. Na przykład, jeżeli podstawy mają odpowiednio 5 m i 3 m, a ramiona mierzą 4 m, obliczamy obwód w następujący sposób:

m = 5,
m = 3,
m = 4.

Obliczenie obwodu wygląda następująco: \( L = 5 + 3 + 2 \times 4 = 16 \, m \).

Zrozumienie wzoru na obwód trapezu oraz jego odmian jest kluczowe dla efektywnego rozwiązywania problemów geometrycznych. Ułatwia również naukę o trapezach i ich właściwościach.

Jakie są inne własności geometryczne trapezu równoramiennego?

Trapez równoramienny wyróżnia się kilkoma istotnymi cechami geometrycznymi, nie tylko poprzez swoje charakterystyczne podstawy i ramiona. Jednym z kluczowych elementów jest linia środkowa, która łączy środki dwóch ramion. Jej długość to dokładnie połowa sumy długości podstaw trapezu, co okazuje się niezwykle pomocne przy różnorodnych obliczeniach.

Symetria trapezu równoramiennego jest wyraźnie widoczna. Kąty przy podstawach są równe, co oznacza, że figura ta jest symetryczna wzdłuż osi biegnącej przez wierzchołki ramion oraz środek podstawy. Co więcej, długości przekątnych są takie same, co dodatkowo podkreśla symetryczny charakter tej figury.

Pomocnicze rysunki, które ilustrują linię środkową czy kąty, znacznie ułatwiają zrozumienie tych właściwości. Dzięki nim można łatwiej zobrazować, jak funkcjonują różne elementy geometryczne w kontekście trapezu. Cechy trapezu równoramiennego mają swoje praktyczne zastosowanie w zadaniach geometrii, co sprawia, że są one niezwykle ważne w naukach ścisłych.

Linia środkowa i jej znaczenie

Linia środkowa trapezu równoramiennego odgrywa istotną rolę w tej figurze geometrycznej. Łączy ona środkowe punkty ramion trapezu i znacząco wpływa na zrozumienie jego właściwości. Długość tej linii wynosi połowę sumy długości podstaw, co oznacza, że jeśli a i b to długości tych podstaw, linia środkowa (M) można obliczyć za pomocą wzoru: M = (a + b) / 2.

Zrozumienie linii środkowej ma kluczowe znaczenie w kontekście obliczeń pola trapezu. Znacznie upraszcza wyznaczanie jego wysokości, zwłaszcza przy zastosowaniu twierdzenia Pitagorasa. Dodatkowo, wspiera różnorodne obliczenia geometryczne, co czyni ją niezwykle pomocną podczas zajęć w szkole czy realizacji projektów.

W praktyce, linia środkowa jest użyteczna w bardziej złożonych obliczeniach oraz interaktywnych zadaniach. Jej zastosowanie może znacznie uprościć proces rozwiązywania problemów. Dzięki tym wskazówkom, można zredukować ryzyko popełnienia błędów w związku z obliczeniami dotyczącymi trapezu równoramiennego.

Symetria figury i rysunki pomocnicze

Symetria trapezu równoramiennego stanowi istotny aspekt jego geometrii. Ta charakterystyczna figura geometryczna wyróżnia się równymi kątami przy podstawach oraz identycznymi długościami przekątnych. Dzięki tym właściwościom trapez posiada oś symetrii, która dzieli go na dwie lustrzane części.

Rysunki pomocnicze odgrywają kluczową rolę w uchwyceniu tych cech. Umożliwiają one lepsze zrozumienie rozmieszczenia kątów oraz osi symetrii. Schematy przedstawiające trapez, które ilustrują oś symetrii oraz przekątne, są doskonałym wsparciem w procesie nauczania i rozwiązywania zadań geometrycznych. Na przykład, graficzna prezentacja pokazująca, jak przekątne tego trapezu łączą się w centralnym punkcie, jest niezwykle pomocna w tworzeniu wzorów oraz odkrywaniu właściwości figury.

Dzięki unikalnej symetrii trapezu równoramiennego łatwo obliczać jego:

pole,
obwód,
oraz inne istotne parametry.

To podkreśla, jak ważne jest stosowanie wizualizacji w geometrii, co znacząco ułatwia zrozumienie złożonych zależności.

Jak zastosować wzór na pole trapezu równoramiennego w zadaniach?

Zrozumienie wzoru na pole trapezu równoramiennego ma zasadnicze znaczenie w matematyce. Wzór ten brzmi następująco:

P = (a + b) * h / 2

Hier „a” i „b” odnoszą się do długości podstaw, a „h” to wysokość figury. Uczniowie często stają przed zadaniami, w których muszą obliczyć pole trapezu, posiadając wartości obu podstaw oraz odpowiadającą im wysokość.

Najczęściej spotykane problemy dotyczą obliczeń pola trapezu w różnych sytuacjach. Na przykład:

często dany jest długość podstaw i wysokość, co umożliwia bezpośrednie zastosowanie wzoru,
w innym przypadku, kiedy mamy do dyspozycji długości ramion i kąt przy podstawie, można sięgnąć po funkcje trygonometryczne, aby również znaleźć poszukiwane pole.

Zrozumienie tego wzoru może być ułatwione dzięki ilustracjom oraz konkretnej praktyce. Dla przykładu, rozważmy trapez, którego podstawy mają długości 8 cm i 12 cm, a wysokość wynosi 5 cm. W tym przypadku obliczenia są proste i prowadzą nas do wyniku:

P = (8 + 12) * 5 / 2 = 50 cm².

Dodatkowo, angażujące zadania, takie jak obliczenia pola przy niepełnych danych, mogą znacznie wzbogacić zdolności uczniów. Wykorzystując tradycyjny wzór w takich kontekstach, uczniowie lepiej przygotowują się na bardziej skomplikowane wyzwania matematyczne, które mogą napotkać w przyszłości.

Najczęstsze typy zadań z trapezem

Najczęściej występujące zadania dotyczące trapezu równoramiennego skupiają się na kilku istotnych aspektach. Do najważniejszych zadań należy obliczanie pola, wysokości oraz obwodu trapezu, a także badanie kątów i przekątnych. Wiele z tych zadań wykorzystuje wzór na pole trapezu:

P = \frac{(a + b) \cdot h}{2},

gdzie a i b oznaczają długości podstaw, a h to jego wysokość.

Oto przykłady klasycznych zadań:

Obliczanie pola trapezu: uczestnicy, korzystając z długości podstaw i wysokości, obliczają pole trapezu, stosując wspomniany wcześniej wzór,
Ustalenie wysokości: na podstawie długości podstaw oraz ramion trapezu, a także wykorzystując twierdzenie Pitagorasa, można wyznaczyć wysokość trapezu,
Wyznaczanie obwodu: uczniowie mają możliwość obliczenia obwodu trapezu równoramiennego, stosując wzór O = a + b + 2c, gdzie c to długość ramienia,
Badanie kątów: uczniowie obliczają miary kątów przy podstawach, opierając się na właściwościach trapezu równoramiennego, co sprawia, że kąty te mają równe wartości,
Wykorzystanie funkcji trygonometrycznych: funkcje te mogą być użyteczne do analizy kątów w trapezie oraz do obliczania jego wymiarów w kontekście układów współrzędnych.

Te różnorodne wyzwania przyczyniają się do głębszego zrozumienia geometrii trapezu równoramiennego, a także rozwijają umiejętności niezbędne do samodzielnego rozwiązywania problemów geometrycznych.

Ilustracje i przykłady rozwiązań

Ilustracje trapezu równoramiennego odgrywają istotną rolę w zrozumieniu jego kształtu i unikalnych właściwości. Rysunki powinny ukazywać zarówno podstawy i ramiona, jak i wysokość, a także przekątne oraz linie środkowe, które doskonale obrazują symetrię tej figury.

Do obliczeń przydatne mogą być przykłady przedstawiające poszczególne kroki:

jak obliczyć pole trapezu, znając długości jego podstaw i ramion,
jak zastosować twierdzenie Pitagorasa, by znaleźć wysokość trapezu.

Rysunki pomocnicze, które prezentują różne przypadki trapezów równoramiennych, są bardzo wartościowe. Przykłady obliczeń mogą zróżnicować konfiguracje, co z kolei pomaga uczniom lepiej pojmować praktyczne zastosowanie wzorów. Te ilustracje i przykłady tworzą mocny fundament dla nauki geometrii, co pozytywnie wpływa na umiejętność rozwiązywania zadań matematycznych.