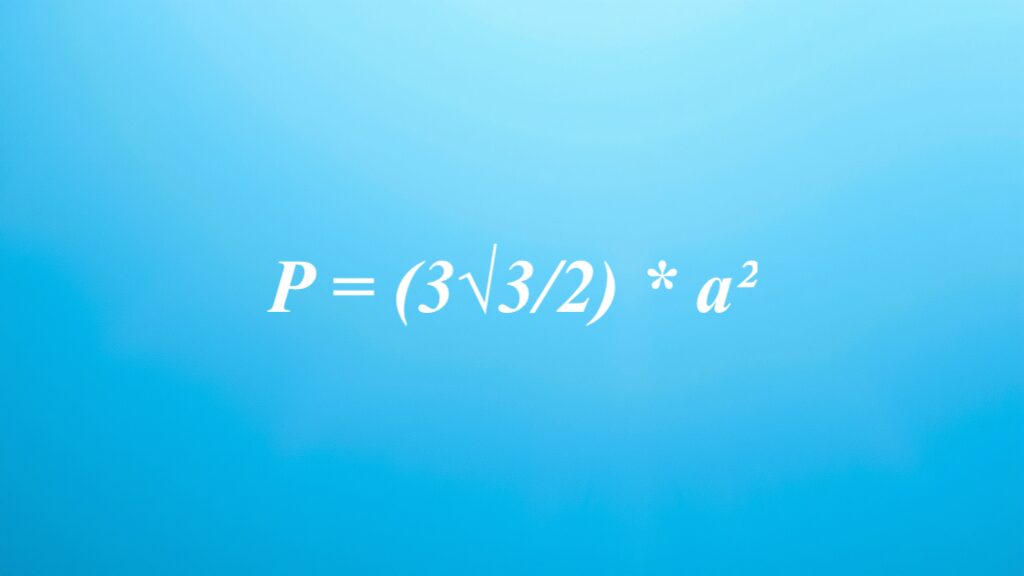Czym jest sześciokąt foremny?
Sześciokąt foremny to figura, która wyróżnia się sześcioma równymi bokami oraz sześcioma kątami wewnętrznymi, z których każdy ma 120 stopni. Należy do kategorii wielokątów foremnych, a jego symetria oraz jednorodne wymiary są jego istotnymi cechami. Co ciekawe, przy zastosowaniu prostych podziałów, taki sześciokąt można rozdzielić na sześć identycznych trójkątów równobocznych, co znacznie upraszcza analizę jego właściwości.
Sześciokąty foremne znajdują zastosowanie w różnych obszarach, zarówno w matematyce, jak i w naszym codziennym funkcjonowaniu. Dzięki swojej symetrii, są chętnie wykorzystywane w:
- architekturze,
- sztuce,
- projektowaniu przedmiotów użytkowych.
Na przykład, płytki inspirowane tą formą łączą walory estetyczne z praktycznością.
Analizując geometryczne właściwości sześciokąta foremnego, takie jak stosunek długości jego boków do promienia okręgu opisanego na tej figurze, odkrywamy, że jest ona niezwykle interesująca z matematycznego punktu widzenia. W konstrukcjach geometrycznych pojawiają się regularne wzory, które są efektem jego symetrycznych cech. Sześciokąt foremny zatem nie tylko odgrywa kluczową rolę w teorii matematycznej, ale także stanowi cenne narzędzie w inżynierii i projektowaniu.
Jakie są właściwości geometryczne sześciokąta foremnego?
Sześciokąt foremny to figura o niezwykle regularnych właściwościach geometrycznych, które odgrywają istotną rolę w matematyce oraz geometrii. Posiada on sześć równych boków i sześć wewnętrznych kątów, z których każdy wynosi 120 stopni. Aby obliczyć obwód tego sześciokąta, wystarczy pomnożyć długość jednego z boków przez sześć.
W tej figurze możemy również wyróżnić przekątne, które dzielimy na:
- długie, które odpowiadają dwukrotności długości boku,
- krótkie, mające wartość równą pierwiastkowi z trzech pomnożonemu przez długość boku.
Taka różnorodność wewnętrznych elementów sprawia, że sześciokąt staje się bardziej złożony i estetyczny.
Jedną z kluczowych cech sześciokąta jest apotema, czyli odległość od środka figury do środka jednego z boków. Długość apotemy jest równa wysokości trójkąta równobocznego, który można skonstruować na bokach sześciokąta. Apotema oraz inne elementy geometryczne, takie jak kąty wewnętrzne i długości przekątnych, wpływają na stabilność, równowagę i symetrię sześciokąta foremnego. Dzięki tym unikalnym cechom figura ta znajduje swoje zastosowanie w wielu dziedzinach, w tym architekturze i inżynierii.
Jakie są kąty wewnętrzne i przekątne w sześciokącie?
Każdy sześciokąt foremny charakteryzuje się swoimi unikalnymi kształtami oraz właściwościami. W tym kształcie każdy z kątów wewnętrznych ma miarę 120 stopni, co wpływa na jego symetrię, nadając mu równowagę i stabilność.
Sześciokąt foremny zawiera dwa typy przekątnych:
- przekątne długie łączą wierzchołki, które dzieli dwóch innych sąsiadów, a ich długość wynosi 2a, gdzie „a” to długość boku sześciokąta,
- przekątne krótkie łączą wierzchołki, które są o jeden wierzchołek oddalone, a ich długość można obliczyć za pomocą wzoru d = √3 * a.
Te unikalne cechy sprawiają, że sześciokąt foremny zyskuje uznanie w wielu dziedzinach, takich jak architektura czy inżynieria. Często można go znaleźć w projektach, które łączą w sobie zarówno symetrię, jak i estetyczne walory.
Jak promień okręgu i apotema odnoszą się do sześciokąta foremnego?
Promień okręgu opisanego na sześciokącie foremnym jest równy długości jego boku. Można więc powiedzieć, że promień okręgu opisanego (R) odpowiada a, gdzie a oznacza długość boku sześciokąta. Z kolei apotema, czyli promień okręgu wpisanego, to odległość od środka sześciokąta do jednego z jego boków. Aby obliczyć apotemę, wykorzystujemy wzór: r = (√3/2) * a.
Te dwa promienie odgrywają kluczową rolę w obliczeniach pól sześciokąta. Możemy obliczyć pole, korzystając z apotemy w innym równaniu:
- P = (apotema × obwód) / 2,
- obwód sześciokąta wynosi 6a,
- co pozwala nam zapisać wzór na pole jako P = (√3/2) * 6a² / 2.
Dzięki tym zależnościom zarówno promień okręgu, jak i apotema ilustrują, w jaki sposób geometria sześciokąta foremnego wpływa na jego pole i budowę.
Jak obliczyć pole sześciokąta foremnego?
Pole sześciokąta foremnego można określić na różne sposoby, w zależności od dostępnych danych. Najbardziej popularną metodą jest użycie długości jego boku. Podstawowy wzór do obliczeń wygląda następująco:
P = (3√3/2) * a².
W tej formule a oznacza długość boku sześciokąta. Ustalono, że pole tego kształtu rośnie w sposób kwadratowy w zależności od długości boku; na przykład, zwiększając bok o 1 jednostkę, pole wzrasta o około 3,07 jednostki kwadratowej.
Inną możliwością jest obliczanie pola na podstawie promienia okręgu, który jest opisany na sześciokącie. Odpowiedni wzór to:
P = 3 * R² * √3,
gdzie R jest promieniem tego rozpatrywanego okręgu. Co więcej, sześciokąt foremny da się podzielić na sześć równobocznych trójkątów, co pozwala na obliczenie pola jako sześciokrotności pola jednego z tych trójkątów.
Kolejną metodą obliczania pola jest wykorzystanie apotemy oraz obwodu. Wzór w tym przypadku wygląda tak:
P = (apotema × obwód) / 2.
Obwód sześciokąta obliczamy jako 6 * a. Apotema to natomiast odległość między środkiem sześciokąta a środkiem jednego z jego boków.
Każda z tych metod pozwala na precyzyjne wyznaczenie pola sześciokąta foremnego, co ma kluczowe znaczenie w wielu dziedzinach, takich jak architektura czy inżynieria.
Jaki jest wzór na pole sześciokąta w zależności od boku?
Obliczanie pola sześciokąta foremnego jest prostym zadaniem, dzięki wzorowi P = (3√3/2) * a², gdzie „a” oznacza długość boku tej figury. Mając to na uwadze, można szybko i precyzyjnie określić pole, korzystając jedynie z informacji o długości boku.
Sześciokąt foremny jest zbudowany z sześciu równobocznych trójkątów. Aby obliczyć pole pojedynczego trójkąta, można zastosować wzór P = (√3/4) * a². Całkowita powierzchnia sześciokąta wynosi sześć razy pole jednego z tych trójkątów, co ilustruje ich powiązanie w ramach geometrii.
Użycie tego wzoru pozwala na szybkie wyznaczenie pola sześciokąta foremnego, co jest niezwykle istotne w różnych dziedzinach, takich jak:
- architektura,
- inżynieria,
- projektowanie przestrzeni.
Zrozumienie i umiejętność zastosowania tego wzoru są nieocenione dla wszystkich zajmujących się geometrią oraz projektowaniem przestrzeni.
Jak wygląda wzór na pole sześciokąta w zależności od promienia okręgu opisanego?
Aby wyznaczyć pole sześciokąta foremnego na podstawie promienia okręgu opisanego, można skorzystać z następującego wzoru:
P = (3√3/2) * R²
W powyższym zapisie P oznacza pole, a R to promień okręgu opisanego. Interesującym jest, że w sześciokącie foremnym długość każdego boku odpowiada długości promienia tego okręgu. Dzięki tej właściwości, promień można bezpośrednio wykorzystać do dokonania obliczeń.
Warto zrozumieć, że geometria sześciokąta, będącego rozszerzeniem okręgu, odgrywa kluczową rolę. Boki i kąty wewnętrzne są ze sobą ściśle powiązane. Na przykład, przyjmując, że
- promień okręgu opisanego wynosi 5,
- możemy obliczyć pole sześciokąta foremnego
- przy użyciu wzoru,
- wprowadzając wartość promienia do wzoru,
- otrzymujemy wynik w postaci około 64,95 jednostek kwadratowych.
Ten wzór jest niezwykle użyteczny, zwłaszcza w kontekście zagadnień geometrycznych oraz zastosowań inżynieryjnych.
Dlaczego pole sześciokąta jest sześciokrotnością pola trójkąta równobocznego?
Pole sześciokąta foremnego można obliczyć poprzez zauważenie, że jest to sześciokrotność pola jednego trójkąta równobocznego. Jak to działa? Sześciokąt można podzielić na sześć identycznych trójkątów. Każdy z tych trójkątów ma pole, które ustalamy korzystając z następującego wzoru:
P = \frac{\sqrt{3}}{4} a^2
gdzie a oznacza długość boku trójkąta.
Sześciokąt zbudowany jest z tych sześciu trójkątów, zatem jego całkowite pole można przedstawić w sposób:
P_{\text{sześciokąt}} = 6 \times P_{\text{trójkąt}}
Podstawiając wcześniej wspomniany wzór, otrzymujemy:
P_{\text{sześciokąt}} = 6 \times \left( \frac{\sqrt{3}}{4} a^2 \right) = \frac{3\sqrt{3}}{2} a^2
To jasno pokazuje, że pole sześciokąta jest równoważne sześciokrotności pola jednego trójkąta równobocznego. Właściwości trójkąta równobocznego bezpośrednio wpływają na obliczanie pola sześciokąta foremnego. Rozbicie figury na trójkąty równoboczne jest kluczowe dla zrozumienia tej relacji.
Jak przeprowadzić wyprowadzenie wzoru na pole sześciokąta?
Wyprowadzenie wzoru na pole sześciokąta foremnego można osiągnąć na dwa zasadnicze sposoby. Oba podejścia wykorzystują cechy trójkąta równobocznego oraz związki między apotemą a obwodem sześciokąta.
Pierwsza z metod polega na podzieleniu sześciokąta na sześć równobocznych trójkątów. Każdy z tych trójkątów ma boki o długości a, co czyni je równobocznymi. Aby obliczyć pole jednego z nich, stosujemy wzór:
P_{trójkąt} = \frac{\sqrt{3}}{4} a^2
Skoro mamy sześć takich trójkątów, pole całego sześciokąta uzyskujemy według wzoru:
P_{sześciokąt} = 6 \times P_{trójkąt} = 6 \times \frac{\sqrt{3}}{4} a^2
Po uproszczeniu, otrzymujemy ostateczny wzór:
P = \frac{3\sqrt{3}}{2} a^2
Druga metoda skupia się na apotezie oraz obwodzie sześciokąta. Apotema to odległość z centrum sześciokąta do jego krawędzi. Pole można określić korzystając ze wzoru:
P = \frac{apotema \times obwód}{2}
Dla sześciokąta foremnego obwód wynosi 6a, co prowadzi nas do kolejnego wzoru na pole:
P = \frac{apotema \times 6a}{2} = 3a \times apotema
Warto zaznaczyć, że znajomość długości apotemy i obwodu jest kluczowa. Dzięki temu możemy łatwiej obliczać pole sześciokąta w różnych sytuacjach. Jeśli posiadamy także promień okręgu opisanego, możemy dostosować wzór, aby uwzględnić tę wartość.
Jak obliczyć pole sześciokąta wpisanego i opisanego?
Aby obliczyć pole sześciokąta wpisanego oraz opisanego, należy posłużyć się kilkoma wzorami, które różnią się w zależności od dostępnych informacji.
- dla sześciokąta foremnym wpisanego w okrąg, pole można wyznaczyć za pomocą długości jego boku (a) oraz wzoru: P = (3√3/2) * a²,
- w długości boku a odpowiada promieniowi okręgu opisanego,
- dla sześciokąta opisanego, który otacza okrąg wpisany, pole obliczamy z promienia tego okręgu, znanego jako apotema (r) z wzoru: P = 3 * r².
Dzięki tym równaniom możemy z dokładnością określić pole sześciokąta. Wybór konkretnego wzoru zależy od posiadanych danych geometrycznych.
Obliczanie pola sześciokąta ma istotne znaczenie w wielu dziedzinach, takich jak architektura, inżynieria czy grafika komputerowa.
Jakie błędy obliczeniowe mogą wystąpić przy liczeniu pola sześciokąta?
Typowe błędy w obliczaniu pola sześciokąta foremnego mają swoje źródło w kilku kluczowych aspektach. Nieprawidłowe użycie wzorów może prowadzić do błędnych wyników, jak na przykład:
- mylenie formuły pole dla sześciokąta z innymi figurami, takimi jak trapez czy romb,
- niewłaściwe podanie długości boku lub promienia okręgu opisanego,
- brak lub niepoprawne stosowanie jednostek miary,
- błędne zaokrąglenia oraz nieprawidłowe obliczanie pierwiastków.
Precyzja, zwłaszcza przy obliczeniach wartości dziesiętnych, jest niezwykle ważna, aby otrzymać właściwy wynik. Dlatego tak istotne jest, aby podchodzić do obliczeń z należytym skupieniem i ostrożnością oraz właściwie stosować wzory, aby uniknąć klasycznych błędów w obliczaniu pola sześciokąta.
Jak wykorzystać wzór na pole sześciokąta w praktyce?
Wzór na pole sześciokąta foremnego odgrywa kluczową rolę w licznych dziedzinach, zwłaszcza w architekturze oraz inżynierii. Umożliwia on szybkie obliczenie powierzchni sześciokątnych elementów, co jest istotne w kontekście projektowania zarówno budynków, jak i różnorodnych konstrukcji. Na przykład, w architekturze wzory sześciokątne często pojawiają się w projektach obiektów, a znajomość ich pola pozwala oszacować zapotrzebowanie na materiały oraz ocenić efektywność strukturalną.
W inżynierii, pole sześciokąta ma znaczenie przy projektowaniu elementów, takich jak:
- panele słoneczne,
- pokrycia dachowe,
- inne elementy konstrukcyjne.
Dzięki umiejętności obliczania tej powierzchni, inżynierowie mogą planować oraz optymalizować zużycie materiałów. Architekci również sięgają po ten wzór w planowaniu przestrzennym, co pozwala im efektywnie zagospodarowywać tereny, zwłaszcza w gęsto zabudowanych miastach.
Zastosowanie tego wzoru nie ogranicza się jedynie do inżynierii. W sztuce sześciokąty często wykorzystywane są w mozaikach i grafice, gdzie przyczyniają się do tworzenia harmonijnych kompozycji. Artyści, inspirowani tymi kształtami, tworzą oryginalne dzieła, które przyciągają wzrok i ukazują matematyczne związki obecne w sztuce.
W końcu, zrozumienie wzoru na pole sześciokąta oraz jego różnorakich zastosowań rozwija techniczne umiejętności, a także pobudza kreatywność w wielu branżach.
Jak pole sześciokąta znajduje zastosowanie w architekturze i inżynierii?
Sześciokąt foremny znajduje zastosowanie w wielu dziedzinach, zwłaszcza w architekturze i inżynierii. Jego wyjątkowe cechy, takie jak doskonała symetria i przestrzenna efektywność, sprawiają, że cieszy się dużym uznaniem. Kształt ten często inspiruje projektantów do tworzenia konstrukcji na wzór plastra miodu. Dzięki niemu można osiągnąć wysoką wytrzymałość przy jednoczesnym minimalnym zużyciu materiałów, co jest szczególnie istotne w budownictwie.
Z racji równomiernego rozkładu sił, elementy sześciokątne doskonale sprawdzają się w projektowaniu:
- paneli,
- płytek,
- konstrukcji nośnych.
Architekci, którzy dążą do harmonii między estetyką a funkcjonalnością, chętnie sięgają po sześciokątne formy w nowoczesnych budynkach, ogrodach czy wystroju wnętrz. Takie kształty można spotkać na przykład w:
- dachach,
- ścianach,
- w różnych miejskich dekoracjach, które wyróżniają się symetrią.
W inżynierii odnaleźć można także zastosowania sześciokątów w projektowaniu maszyn i urządzeń, gdzie stabilność oraz oszczędność materiałów mają kluczowe znaczenie. Co więcej, w dziedzinach takich jak aerodynamika i hydrodynamika, efektywne projektowanie korzysta z sześciokątnych kształtów, co przekłada się na poprawę właściwości przepływu. Takie innowacyjne podejścia doskonale wpisują się w minimalistyczne i praktyczne trendy współczesnej architektury i inżynierii.
Jakie są przykłady zastosowań pola sześciokąta w sztuce?
Sześciokąt foremny cieszy się różnorodnymi zastosowaniami w sztuce, co jest zasługą jego niepowtarzalnych cech estetycznych i geometrycznych. Na przykład, jego powierzchnia często staje się elementem mozaik, gdzie sześciokąty łączą się, tworząc różnorodne wzory i harmonijne kompozycje. Co więcej, geometryczne aranżacje oparte na sześciokącie można podziwiać w architekturze i designie, gdyż podkreślają one symetrię oraz równowagę w artystycznych projektach.
Dodatkowo, dekoracyjne ornamenty inspirowane tym kształtem wzbogacają wygląd nie tylko budynków, ale również mebli i innych dzieł sztuki. Jego regularne formy znalazły również swoje miejsce w nowoczesnej sztuce, gdzie wykorzystywane są do tworzenia przestrzennych struktur. Te cechy sprawiają, że sześciokąt foremny staje się symbolem harmonii, co czyni go wyjątkowym motywem w rozmaitych stylach artystycznych.