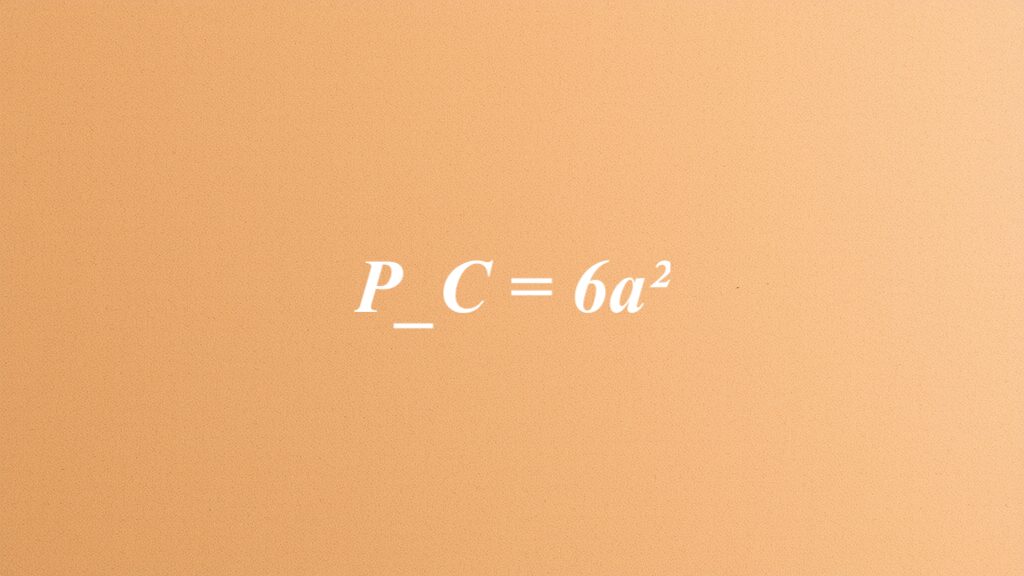Wzór na pole sześcianu

Co to jest sześcian?

Sześcian, nazywany również kostką, to fascynujący obiekt trójwymiarowy, który można spotkać w geometrii. Składa się z sześciu identycznych kwadratowych ścian, a każda z jego krawędzi ma równą długość. Dzięki temu figura ta odznacza się niezwykłą symetrią. Oprócz ścian, sześcian dysponuje 12 krawędziami oraz 8 wierzchołkami, co czyni go istotną bryłą w świecie geometrii.

Z perspektywy formalnej sześcian jest regularnym wielościanem, co oznacza, że wszystkie jego ścianki mają identyczny kształt – kwadratu. Warto podkreślić, że sześcian ma wyjątkowe właściwości symetryczne; jest zarówno symetryczny przy obrotach, jak i odbiciach, co czyni go intrygującym obiektem badań w dziedzinie teorii symetrii. Te cechy umacniają jego znaczenie w licznych dziedzinach, od matematyki po architekturę.

Zastosowania sześcianu są naprawdę różnorodne. Oprócz działań związanych z geometrią, wykorzystuje się go również w:

• modelowaniu przestrzennym,
• inżynierii,
• naukach przyrodniczych,
• edukacji z zakresu geometrii.
• rozwiązywaniu bardziej skomplikowanych koncepcji przestrzennych.

Dzięki sześcianowi uczniowie mogą lepiej zrozumieć bardziej skomplikowane koncepcje przestrzenne, co czyni go niezbędnym elementem w procesie nauczania.

Jakie są właściwości sześcianu?

Sześcian to fascynująca bryła przestrzenna, wyróżniająca się wieloma ciekawymi właściwościami. Na pierwszym planie mamy sześć identycznych ścian w kształcie kwadratów. Każda z nich ma pole równe a², gdzie 'a’ to długość boku sześcianu. Oprócz tego, sześcian charakteryzuje się 12 krawędziami i 8 wierzchołkami, co sprawia, że jego budowa jest zarówno prosta, jak i doskonała.

Jednym z najważniejszych atutów sześcianu jest jego niezwykła symetria. Posiada on symetrię obrotową oraz odbicia, co oznacza, że możemy go obracać lub odbijać w różnych płaszczyznach, a jego kształt i wymiary pozostaną niezmienne. Co więcej, suma długości wszystkich krawędzi sześcianu wynosi 12a, co jest niezwykle istotne przy obliczeniach związanych z jego właściwościami.

Te cechy sprawiają, że sześcian znajduje szerokie zastosowanie w wielu dziedzinach:

• architektura,
• modele geometryczne,
• projekty edukacyjne,
• symulacje komputerowe,
• elementy sztuki.

Zrozumienie jego charakterystyki jest kluczowe dla praktycznych zastosowań, a także przyczynić się może do lepszego zgłębienia tematyki geometrii.

Z czego składa się sześcian?

Sześcian, będący trójwymiarową bryłą, ma sześć identycznych kwadratowych ścian. Powierzchnia każdej z nich to a², gdzie a oznacza długość jednego boku sześcianu. Ciekawostką jest, że wszystkie krawędzie sześcianu mają tę samą długość, co gwarantuje, że każda ściana jest w pełni wymiarowa.

Łączna długość wszystkich krawędzi wynosi 12a, ponieważ sześcian dysponuje dokładnie 12 krawędziami. Dodatkowo, istnieje coś takiego jak siatka sześcianu, czyli dwuwymiarowy model, który pokazuje, jak te sześć kwadratów jest rozmieszczonych na jednej płaszczyźnie. To wizualne przedstawienie ułatwia zrozumienie i wyobrażenie sobie, jak naprawdę wygląda sześcian.

Jak oblicza się pole jednej ściany sześcianu?

Aby obliczyć pole jednej ze ścian sześcianu, musimy najpierw zwrócić uwagę na właściwości kwadratu, który tę ścianę tworzy. Każdy bok kwadratu ma długość równą długości krawędzi sześcianu. Wzór na obliczenie pola tej figury to P_p = a², gdzie „a” stanowi długość boku sześcianu.

Obliczenie pola polega na prostym pomnożeniu długości boku przez samą siebie. Na przykład, jeżeli krawędź sześcianu liczy sobie 4 jednostki, pole jednej ściany możemy wyznaczyć, wykonując obliczenie 4², co daje nam 16 jednostek kwadratowych.

Warto zauważyć, że wszystkie sześć ścian sześcianu ma to samo pole. Dlatego też obliczenie pola jednej z nich jest kluczowe dla wyznaczenia całkowitej powierzchni sześcianu. To pierwsze działanie stanowi fundament dla dalszego obliczania całkowitego pola powierzchni tej bryły.

Jaki jest wzór na pole sześcianu?

Wzór na pole powierzchni sześcianu umożliwia nam obliczenie całkowitej powierzchni tego kształtu geometrycznego. Obliczamy to według równania: P_C = 6a², gdzie „a” oznacza długość krawędzi sześcianu. Sześcian składa się z sześciu identycznych ścian, z których każda ma kształt kwadratu o boku równym a.

Każda ze ścian ma pole wynoszące a². Ponieważ mamy sześć takich ścian, aby znaleźć całkowitą powierzchnię, mnożymy pole jednej z nich przez sześć. Dlatego też używamy wzoru P_C = 6a². Jest on niezwykle istotny w różnych dziedzinach, takich jak:

• architektura,
• inżynieria,
• matematyka.

Warto zaznaczyć, że ten wzór ma zastosowanie uniwersalne. Możemy go stosować dla każdego sześcianu, niezależnie od jego wymiarów, o ile znamy długość krawędzi. Tak więc równanie to często pojawia się w zadaniach matematycznych, ułatwiając rozwiązywanie problemów dotyczących objętości oraz innych właściwości sześcianu.

Jak wyprowadzić wzór na pole sześcianu?

Aby obliczyć pole sześcianu, najpierw przyjrzyjmy się jego budowie. Sześcian składa się z sześciu identycznych kwadratowych ścianek, a długość krawędzi każdej z nich wynosi „a”. Pole powierzchni jednej ściany można łatwo policzyć, stosując wzór:

P₁ = a².

Biorąc pod uwagę, że istnieje sześć takich ścian, całkowite pole powierzchni sześcianu, oznaczane jako P_C, można zapisać jako sumę pól wszystkich sześciu ścianek:

P_C = P₁ + P₁ + P₁ + P₁ + P₁ + P₁, co upraszcza się do 6 × a².

Z tego powodu wzór na pole sześcianu można zwięźle określić jako:

P_C = 6a².

Dzięki temu prostemu równaniu jesteśmy w stanie szybko obliczyć pole powierzchni sześcianu, znając wyłącznie długość jego boku.

Co oznacza zapis P_C = 6a²?

Zapis \( P_C = 6a² \) to matematyczny sposób na określenie całkowitej powierzchni sześcianu. Wskazuje on, że pole zewnętrzne tej figury trójwymiarowej jest sześciokrotnością powierzchni pojedynczej ściany. Każda ze ścian sześcianu ma pole równe \( a² \), gdzie \( a \) oznacza długość jednej krawędzi.

Dzięki temu wzorowi, obliczenie całkowitego pola powierzchni sześcianu staje się znacznie łatwiejsze, co jest niezwykle pomocne w geometrii. Wystarczy:

1. podnieść długość krawędzi do kwadratu,
2. pomnożyć przez sześć.

Na przykład, jeśli mamy sześcian z krawędzią o długości 2, obliczenie jego powierzchni wygląda następująco:

\[ P_C = 6 \times (2)² = 24 \]

co oznacza, że otrzymujemy 24 jednostki kwadratowe.

Ten wzór jest nie tylko praktyczny, ale również bardzo istotny w kontekście zadań matematycznych dotyczących figur przestrzennych oraz ich właściwości.

Jak działa wzór na pole powierzchni całkowitej sześcianu?

wzór na całkowite pole powierzchni sześcianu, napisany jako P_C = 6a², opiera się na prostym założeniu. Aby obliczyć całkowite pole, wystarczy pomnożyć pole jednej z sześciu identycznych ścian (a²) przez 6. Dzięki tej efektywnej metodzie możemy szybko uzyskać rezultat.

Obliczanie pola pojedynczej ściany sześcianu polega na zastosowaniu formuły a², gdzie 'a’ reprezentuje długość boku. Mnożenie pola jednej ściany przez 6 pozwala nam uzyskać łączne pole wszystkich ścian, co prowadzi do precyzyjnego wyniku dla całkowitej powierzchni sześcianu.

Podczas obliczeń warto pamiętać o odpowiednich jednostkach miary, takich jak:

• centymetry,
• metry,
• cale.

To pozwala na uzyskanie ostatecznego wyniku w właściwych jednostkach, na przykład w centymetrach kwadratowych (cm²).

Dlaczego mnożymy przez 6?

Mnożymy przez sześć, ponieważ sześcian składa się z sześciu takich samych, kwadratowych ścian. Aby obliczyć jego całkowite pole powierzchni, summujemy pola wszystkich tych ścian. Pole jednej z nich wyliczamy za pomocą wzoru a², gdzie a oznacza długość boku sześcianu. Dlatego całkowite pole powierzchni sześcianu wynosi 6a².

Dzięki temu podejściu możemy w prosty sposób uwzględnić wszystkie ściany, co jest kluczowe przy analizie geometrii sześcianu. Zawsze pamiętamy o sześciu ścianach, co stanowi fundament wzoru na pole powierzchni całkowitej.

Jakie jednostki stosuje się przy obliczaniu pola sześcianu?

Podczas obliczania powierzchni sześcianu używamy jednostek kwadratowych, takich jak centymetry kwadratowe (cm²) oraz metry kwadratowe (m²). Wybór przedmiotu miary jest uzależniony od długości boku sześcianu, oznaczonego literą (a), który jest podstawą naszych obliczeń.

Na przykład, jeżeli długość boku sześcianu wynosi 2 cm, pole powierzchni obliczamy w centymetrach kwadratowych. W tym przypadku wynik to:

• 6 * (2 cm)², co daje nam 24 cm².

Z kolei, gdy długość boku osiąga 3 m, przeliczenia dokonujemy w metrach kwadratowych, co prowadzi do wyniku:

• 6 * (3 m)², czyli 54 m².

Dokładne dobieranie jednostek miary odgrywa kluczową rolę w uzyskiwaniu precyzyjnych rezultatów. Warto więc pamiętać o stosowaniu odpowiednich jednostek przy każdym obliczeniu.

Jak obliczyć pole sześcianu krok po kroku?

Aby obliczyć powierzchnię sześcianu, wystarczy postępować zgodnie z poniższymi wskazówkami:

1. Zacznij od pomiaru długości krawędzi – Na początku zmierz długość krawędzi sześcianu, którą będziemy oznaczać literą „a”.
2. Oblicz pole jednej z powierzchni – Następnie określ pole jednej ścianki sześcianu za pomocą wzoru: \(P_p = a²\). Ten wynik odnosi się do pojedynczej ścianki.
3. Przemnóż przez 6 – Na końcu, aby uzyskać całkowite pole, pomnóż pole jednej ścianki przez 6, ponieważ sześcian składa się z sześciu identycznych ścian. Równanie przedstawia się w ten sposób: \(P_C = 6a²\).

Te trzy etapy są kluczowe do efektywnego obliczenia pól sześcianu. Metodologia ta nie tylko jest prosta, ale również bazuje na właściwościach sześcianu, co czyni uzyskane wyniki wartościowymi w licznych zadaniach matematycznych.

Kiedy stosujemy wzór na pole sześcianu w zadaniach matematycznych?

Wzór na pole powierzchni sześcianu to \( P_C = 6a^2 \). To równanie wykorzystujemy w matematyce do obliczania całkowitego obszaru bryły, która ma równe krawędzie i której ściany przyjmują formę kwadratów. Najczęściej pojawia się w kontekście geometrii przestrzennej. W różnorodnych zadaniach często zadajemy sobie pytanie o powierzchnię sześcianu, zwracając uwagę na problemy związane z jego objętością lub długościami krawędzi.

W praktyce ten wzór okazuje się niezwykle użyteczny w procesie nauczania, wspierając uczniów w zrozumieniu podstaw geometrii. Przykłady zadań mogą dotyczyć obliczeń dotyczących rzeczywistych przedmiotów, takich jak:

• kostki do gry,
• sześcienne pojemniki,
• meble w formie sześcianów.

Dzięki temu uczniowie uczą się, jak zastosować wzór na pole powierzchni sześcianu w różnych kontekstach, co pozwala im lepiej pojąć geometryczne cechy obiektów w trójwymiarowej przestrzeni.

Przykłady obliczeń pola sześcianu

Przykłady dotyczące obliczania pola powierzchni sześcianu wykorzystują formułę P_C = 6a², gdzie „a” reprezentuje długość boku sześcianu. Te obliczenia ukazują, w jaki sposób długość krawędzi wpływa na całkowitą powierzchnię.

Dla boku o długości 3 cm możemy obliczyć pole sześcianu w następujący sposób:

P_C = 6 * (3 cm)² = 6 * 9 cm² = 54 cm².

Gdy jednak weźmiemy pod uwagę bok równy 4 cm, wykonujemy następujące obliczenia:

P_C = 6 * (4 cm)² = 6 * 16 cm² = 96 cm².

A dla sześcianu z bokiem o długości 5 cm mamy:

P_C = 6 * (5 cm)² = 6 * 25 cm² = 150 cm².

Te trzy przypadki pokazują, że pole powierzchni sześcianu rośnie wraz z wydłużeniem boku. Zmiana długości boku o 1 cm skutkuje różnicą wynoszącą 42 cm² – to różnica pomiędzy polem sześcianu o boku 3 cm a sześcianu o boku 5 cm. Jak widać, jest to znaczny wzrost całkowitej powierzchni.

Takie obliczenia znajdują zastosowanie w licznych zadaniach matematycznych, co pokazuje praktyczną wartość wzoru P_C = 6a².

Jak interpretować wyniki obliczeń?

Interpretacja wyników dotyczących pola sześcianu polega na obliczeniu całkowitej powierzchni wszystkich sześciu jego ścian. Analizując te wyniki, możemy lepiej zrozumieć, jak pole powierzchni zmienia się w zależności od długości boku tego wielościanu. Wzrost długości boku skutkuje zwiększeniem pola powierzchni w kwadracie tej wartości.

Na przykład, gdy bok sześcianu ma długość 2 cm, pole jednej ściany wynosi 4 cm², co w sumie daje 24 cm² jako całkowite pole całej bryły. Z tego wynika, że zmieniając długość boku, pole powierzchni zmienia się w sposób nieliniowy. Tego typu interpretacja wyników jest niezwykle istotna w praktycznych zastosowaniach, takich jak inżynieria i architektura. W tych dziedzinach zrozumienie relacji między wymiarami a polem powierzchni ma kluczowe znaczenie dla efektywnego projektowania.

Ponadto, porównując różnorodne sześciany, znajomość tego, jak pole powierzchni zwiększa się wraz ze wzrostem długości boku, ułatwia oceny i porównania dotyczące ich powierzchni. To zagadnienie ma znaczenie w wielu aspektach praktycznego zastosowania.

Typowe zadania z polem sześcianu

Typowe zadania dotyczące pola powierzchni sześcianu są kluczowym elementem w nauce geometrii w szkołach. Aby obliczyć pole powierzchni sześcianu, stosuje się wzór P_C = 6a², gdzie a to długość krawędzi sześcianu. W matematycznych wyzwaniach uczniowie często porównują pola różnych sześcianów lub obliczają pole na podstawie konkretnej długości krawędzi.

Na przykład, w jednym z zadań można obliczyć pole sześcianu o krawędzi mierzącej 4 cm. W tym przypadku obliczenia przebiegają w następujący sposób:

P_C = 6(4 cm)², co oznacza, że 6 x 16 cm² daje nam 96 cm². Istnieje również wiele innych przykładów z różnymi długościami krawędzi, które pomagają w lepszym zrozumieniu tego wzoru oraz jego zastosowania w praktyce.

Dodatkowo, aby jeszcze głębiej poznać temat, warto rozwiązywać zadania, które wymagają wykorzystania wzoru w rzeczywistych sytuacjach. Na przykład:

• można obliczyć, ile materiału będzie potrzebne do pokrycia powierzchni sześcianu,
• ćwiczenia te utrwalają zdobytą wiedzę,
• pokazują, jak geometria ma zastosowanie w codziennym życiu.

Jak pole sześcianu odnosi się do innych wymiarów i własności?

Pole sześcianu jest ściśle związane z innymi jego wymiarami oraz właściwościami. Na przykład długość przekątnej, obliczana ze wzoru d = a√3, ukazuje, jak złożoną strukturę ma ten geometryczny obiekt. To kluczowy element, gdy chodzi o obliczenia związane z polem powierzchni i objętością.

Objętość sześcianu, wyrażona jako V = a³, także jest ściśle związana z jego wymiarami. Warto zauważyć, że:

• promień kuli wpisanej w sześcian to połowa długości jego krawędzi, co przedstawia się jako r = a/2,
• promień kuli opisanej można obliczyć, korzystając z długości przekątnej, a jego wzór to R = d/2,
• co po przekształceniu daje R = (a√3)/2.

Te relacje pomiędzy wymiarami sześcianu, polem powierzchni, objętością oraz promieniami kul są niezwykle istotne. Ich zrozumienie pozwoli lepiej stosować odpowiednie wzory w różnorodnych zadaniach matematycznych oraz praktycznych zastosowaniach geometrii.

Jaka jest długość przekątnej sześcianu?

Długość przekątnej sześcianu można z łatwością obliczyć, korzystając z wzoru: d = a√3, gdzie a oznacza długość krawędzi sześcianu. Ta przekątna łączy przeciwległe wierzchołki i zawsze jest dłuższa zarówno od krawędzi, jak i przekątnej podstawy.

Aby lepiej zrozumieć tę relację, warto sięgnąć po Twierdzenie Pitagorasa. W przypadku sześcianu to twierdzenie obejmuje aż trzy wymiary. Można zauważyć, że długość przekątnej jest o czynnik √3 większa od długości pojedynczej krawędzi, co ukazuje, jak długość wzrasta w proporcjonalny sposób w trzech wymiarach. Dodatkowo, istotne jest, że długość boku sześcianu ma kluczowe znaczenie dla obliczenia przekątnej, wpływając na całkowite proporcje i rozmiary tej figury.

Jak obliczyć objętość sześcianu?

Aby obliczyć objętość sześcianu, wystarczy zastosować prosty wzór, czyli V = a³. W tej formułce V reprezentuje objętość, natomiast a to długość krawędzi tego geometrycznego kształtu. Objętość sześcianu wskazuje, jaką przestrzeń zajmuje w trójwymiarowym wymiarze.

Na przykład, gdy krawędź sześcianu wynosi 3 cm, jego objętość obliczymy w następujący sposób:

V = 3³ = 3 × 3 × 3 = 27 cm³.

Warto także podkreślić, że objętość sześcianu odgrywa kluczową rolę jako miara przestrzeni. Zrozumienie tego wzoru jest zatem niezbędne w kontekście obliczeń związanych z objętością obiektów trójwymiarowych.

Czy istnieje zależność między polem a objętością sześcianu?

Związek pomiędzy polem a objętością sześcianu jest istotnym zagadnieniem w matematyce i geometrii. Aby lepiej to zrozumieć, warto zapoznać się z odpowiednimi wzorami:

• Pole powierzchni sześcianu: obliczane według wzoru P_C = 6a², uzależnione od długości jego boku, oznaczanego jako a,
• Objętość sześcianu: wyraża się wzorem V = a³,
• Proporcjonalność: pole wzrasta w proporcji do kwadratu długości krawędzi,
• Wpływ zmian: nawet niewielka zmiana długości krawędzi może wywołać znaczny przyrost objętości,
• Przykład: podwajając długość boku z a na 2a, pole powierzchni zwiększa się czterokrotnie, podczas gdy objętość rośnie aż osiem razy.

Zatem, zmiany długości boku sześcianu wpływają w różny sposób na jego pole powierzchni i objętość. Ta zależność ma kluczowe znaczenie w wielu praktycznych zastosowaniach oraz przy rozwiązywaniu problemów geometrycznych. Zrozumienie tych relacji ułatwia pracę z figurami geometrycznymi i ich właściwościami.

Jak policzyć promień kuli opisanej i wpisanej na podstawie długości boku?

Promień kuli wpisanej w sześcian to połowa długości jego krawędzi. Możemy to zapisać jako r = a/2, gdzie „a” oznacza długość boku sześcianu. Z tego wynika, że gdy bok sześcianu staje się dłuższy, promień jego kuli wpisanej również rośnie.

Promień kuli opisanej obliczamy na podstawie długości przekątnej sześcianu. Przekątną można wyznaczyć za pomocą wzoru (a√3), co prowadzi do obliczenia promienia kuli opisanej jako R = (a√3)/2. Taka kula może być umiejscowiona wokół sześcianu w taki sposób, że styka się ze wszystkimi jego wierzchołkami.

Zrozumienie tych zależności jest kluczowe w dziedzinach takich jak geometria oraz inżynieria. Ułatwia to przeprowadzanie bardziej zaawansowanych obliczeń, które są związane z bryłami.

Jakie są zastosowania wzoru na pole sześcianu w geometrii?

Wzór na pole sześcianu, P_C = 6a², ma liczne zastosowania w różnych dziedzinach, takich jak geometria, architektura czy inżynieria. Jego praktyczne znaczenie staje się szczególnie widoczne przy projektowaniu przestrzeni oraz tworzeniu rozmaitych obiektów.

W architekturze umiejętność obliczania pola sześcianu jest niezbędna do:

• określenia powierzchni ścian budynków,
• wyboru odpowiednich materiałów budowlanych,
• precyzyjnego oszacowania kosztów.

Z kolei inżynierowie korzystają z tego wzoru, aby lepiej zrozumieć wymiary przestrzeni, co ma kluczowe znaczenie w kontekście obliczeń dotyczących objętości i potrzebnych materiałów.

Zastosowania wzoru na pole sześcianu sięgają daleko poza teorie; jest on istotny w projektach inżynieryjnych, które wymagają szczegółowych obliczeń. Dodatkowo, pomocny jest także dla uczniów uczących się geometrii przestrzennej, umożliwiając im grubsze pojmowanie kształtów i ich charakterystyk.

Na co dzień pole sześcianu znajduje odzwierciedlenie w wielu przedmiotach, takich jak:

• kostki do gry,
• pudełka,
• inne regularne obiekty.

W każdej sytuacji, gdzie potrzebne jest obliczenie powierzchni sześcianu, ten wzór staje się niezwykle użytecznym narzędziem, zarówno w teoretycznych rozważaniach, jak i praktycznych zastosowaniach.

Gdzie spotykamy pole sześcianu w praktyce?

Pole sześcianu ma wiele różnych zastosowań, które znajdują się w wielu dziedzinach. W budownictwie obliczenie powierzchni sześcianu jest niezwykle istotne — pomaga określić, ile materiału będziemy potrzebować do wykończenia ścian, dachów czy fundamentów. W inżynierii ten sam wzór jest bardzo przydatny, ponieważ umożliwia analizowanie struktur i obiektów, co znacznie ułatwia proces projektowania i optymalizacji przestrzeni.

Przykładowo, w projektowaniu opakowań pole sześcianu ma kluczowe znaczenie, zwłaszcza podczas tworzenia pudełek i kontenerów. Dokładne obliczenia dot. materiałów są niezbędne, aby proces produkcji był efektywny. W kontekście edukacji matematycznej uczniowie odkrywają właściwości sześcianu, co pozwala im lepiej zrozumieć geometrię trójwymiarową oraz rozwija umiejętności w zakresie rozwiązywania problemów związanych z przestrzenią.

Widać zatem, że pole sześcianu znajduje szerokie zastosowanie praktyczne, wpływając na różne aspekty:

• budownictwa,
• inżynierii,
• projektowania,
• edukacji.

Jakie błędy często pojawiają się przy obliczaniu pola sześcianu?

Podczas obliczania pola sześcianu można napotkać wiele typowych pomyłek, które mogą prowadzić do błędnych rezultatów. Oto kilka najczęstszych problemów, z którymi można się spotkać:

• błędne pomiary długości boku – Niekiedy długość boku sześcianu jest źle mierzona lub podawana, co bezpośrednio wpływa na końcowy wynik obliczeń,
• problemy z podnoszeniem do kwadratu – Podczas wyliczania pola powierzchni, często popełniany jest błąd w podnoszeniu długości boku do kwadratu. Nie zapominaj, że pole to a²,
• pomijanie mnożenia przez 6 – Sześcian posiada sześć identycznych ścian, dlatego pominięcie mnożenia przez 6 skutkuje zaniżonym wynikiem,
• niewłaściwe jednostki – Użycie nieodpowiednich jednostek, takich jak m zamiast cm, może sprawić, że końcowy rezultat będzie błędny w kontekście poszukiwanych jednostek.

Aby ustrzec się przed tymi pomyłkami, warto trzymać się właściwych wzorów na pole sześcianu. Dobrze jest również upewnić się, że pomiary oraz jednostki są odpowiednie. Dzięki takiemu podejściu uzyskasz dokładne wyniki w obliczeniach matematycznych.