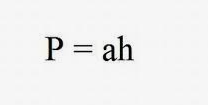Wzór na pole równoległoboku

Równoległobok to ciekawa figura geometryczna, która należy do rodziny czworokątów. Charakteryzuje się dwiema parami boków, które są równoległe i mają identyczną długość. Przekątne tego kształtu, będące kluczowymi elementami, krzyżują się w punkcie, dzieląc je dokładnie na pół. Dzięki tym cechom równoległobok jest jedną z fundamentalnych figur w geometrii, a jego zastosowania można dostrzec w różnych dziedzinach nauki oraz w codziennym życiu.

Figura ta składa się z czterech wierzchołków, a długości boków można łatwo wyznaczyć. Obwód równoległoboku oblicza się, dodając długości wszystkich jego boków. Istnieje wiele rodzajów równoległoboków, na przykład:

prostokąty,
romby.

Zgłębienie wiedzy o równoległoboku oraz jego podstawowych elementach, takich jak wymiary boków i kąty, jest istotne przy wyliczaniu powierzchni. Dzięki znajomości odpowiednich parametrów można skutecznie aplikować różne wzory na pole tej figury. Tego typu obliczenia mają szerokie zastosowanie w praktyce, w tym w dziedzinach takich jak architektura.

Podstawowe elementy równoległoboku

Podstawowe cechy równoległoboku obejmują kilka istotnych aspektów geometrucznych. Przede wszystkim mówimy o długościach boków, które oznaczamy jako a i b. Bok a reprezentuje długość jednej z podstaw, natomiast bok b to długość drugiej, przeciwległej podstawy. Wysokość równoległoboku, oznaczana literą h, to odległość mierzona prostopadle od podstawy do naprzeciwległego boku.

Nie można zapominać o kątach wewnętrznych, które także wnoszą wiele do charakterystyki równoległoboku. Ich suma zawsze wynosi 360°. Kąty przyległe są sobie równe, podczas gdy kąty naprzemianległe mają swoiste relacje, które wpływają na właściwości całego kształtu. Warto również zwrócić uwagę na przekątne – d₁ i d₂, które przecinają się w centrum równoległoboku. To również ważny element do analizy geometrycznej.

Elementy, o których wspomniano – długości boków, wysokość, kąty oraz przekątne – są kluczowe dla pełnego zrozumienia i obliczenia pola powierzchni równoległoboku. Te obliczenia mają ogromne znaczenie nie tylko w teorii matematycznej, ale także w praktycznych zastosowaniach geometrycznych.

Czym równoległobok różni się od innych czworokątów?

Równoległobok wyróżnia się spośród innych czworokątów, takich jak trapez czy romb, przede wszystkim swoją unikalną budową. Posiada dwie pary boków, które są równoległe i mają identyczną długość, co sprawia, że wszystkie jego boki biegną w jednym kierunku. To nadaje temu kształtowi wyjątkowy charakter.

W przeciwieństwie do trapezu, który dysponuje jedynie jedną parą równoległych krawędzi, równoległobok cechuje się bardziej złożoną strukturą geometryczną. Kolejną interesującą właściwością równoległoboku jest to, że jego przekątne przecinają się w punkcie środkowym, co stanowi znaczący element jego definicji.

Romb, będący szczególnym przypadkiem równoległoboku, ma z kolei wszystkie boki takie same, a jego kąty mogą różnić się od prostych. Te subtelne różnice są istotne, zwłaszcza gdy chodzi o praktyczne zastosowania oraz obliczenia pola równoległoboku w porównaniu z innymi figurami płaskimi.

Równoległoboki znajdują szerokie zastosowanie w architekturze oraz inżynierii, gdzie ich właściwości strukturalne odgrywają kluczową rolę przy projektowaniu różnorodnych budowli. Dlatego czasami to, jak różnią się te kształty, ma nie tylko teoretyczne znaczenie, ale także praktyczne konsekwencje w wielu dziedzinach.

Jakie są wzory na pole równoległoboku?

Pole równoległoboku można obliczyć na różne sposoby, w zależności od tego, co mamy do dyspozycji.

Najprostszy sposób to zastosowanie wzoru P = a × h, gdzie „a” to długość podstawy, a „h” to wysokość spuszczona na tę podstawę. Idealnie sprawdza się to, gdy znamy wartość wysokości.

Inną metodą, gdy posiadamy długości dwóch sąsiednich boków oraz kąt między nimi, jest użycie wzoru P = a × b × sin α. W tej sytuacji „b” oznacza długość drugiego boku, a „sin α” to sinus kąta α. Ta technika jest precyzyjna i wykorzystuje zasady trigonometrii.

Jeżeli mamy do czynienia z przekątnymi równoległoboku, warto zastosować wzór P = 1/2 × d₁ × d₂ × sin γ. W nim „d₁” oraz „d₂” to długości przekątnych, podczas gdy „sin γ” odnosi się do sinusa kąta między nimi. Tego typu podejście jest szczególnie użyteczne, gdy jedynymi znanymi danymi są długości przekątnych.

Każda z tych metod obliczania pola równoległoboku ma swoje zastosowanie w różnych kontekstach. Dlatego zagadnienie to często pojawia się zarówno w matematyce, jak i inżynierii. Wybór właściwego wzoru znacząco ułatwia przeprowadzenie dokładnych i efektywnych obliczeń.

Wzór P = a × h

Wzór P = a × h jest fundamentalnym narzędziem do obliczania pola równoległoboku. W tym równaniu „P” oznacza pole, „a” to długość podstawy, natomiast „h” to wysokość. Wysokość mierzy się jako odległość prostopadła od podstawy do przeciwległego boku. Dzięki temu prostemu wzorowi, możemy szybko wyliczyć pole równoległoboku, co jest niezwykle istotne w geometrii.

Obliczenie pola jest bardzo łatwe, zwłaszcza gdy mamy dane długości podstawy i wysokości. Na przykład, przy długości podstawy wynoszącej 5 cm i wysokości 4 cm, pole obliczamy jako P = 5 cm × 4 cm, co daje nam 20 cm².

Wzór P = a × h znajduje szerokie zastosowanie w różnych dziedzinach, takich jak:

architektura,
inżynieria,
branże związane z geometrią.

Dokładność tych obliczeń ma kluczowe znaczenie w profesjonalnej praktyce. Zrozumienie wymiarów równoległoboku umożliwia precyzyjne i szybkie wyznaczanie pola, co jest wartościowe zarówno w edukacji, jak i w karierze zawodowej.

Wzór P = a × b × sin α

Wzór P = a × b × sin α to niezwykle przydatne narzędzie do obliczania pola równoległoboku. W tej formule „a” i „b” oznaczają długości dwóch przyległych boków, a α to kąt, jaki tworzą. Element „sin” odnosi się do wartości sinusa kąta, co pomaga w określeniu odpowiedniej wielkości pola.

Kiedy zechcesz skorzystać z tego wzoru, ważne jest, aby znać długości boków oraz miarę kąta. Jeśli wysokość równoległoboku jest trudna do zmierzenia, wzór P = a × b × sin α staje się efektywnym sposobem na obliczenie pola. Na przykład:

przy długości boku „a” wynoszącej 5 cm oraz boku „b” równej 7 cm, gdy kąt α ma 30°, pole równoległoboku obliczymy w następujący sposób:

P = 5 cm × 7 cm × sin(30°) = 5 cm × 7 cm × 0,5 = 17,5 cm².

To podejście okazuje się niezwykle pomocne w geometrii, gdzie pomiar wszystkich wysokości bywa wyzwaniem. Znajduje szerokie zastosowanie nie tylko w trygonometrii, ale również w różnych obszarach inżynierii, architektury i nauczania.

Wzór P = 1/2 × d₁ × d₂ × sin γ

Wzór P = 1/2 × d₁ × d₂ × sin γ odgrywa fundamentalną rolę w obliczaniu pola równoległoboku. Opiera się on na długościach przekątnych, oznaczonych jako d₁ i d₂, oraz kącie γ, który je łączy. Kluczowe znaczenie ma tutaj sinus tego kąta, ponieważ przyczynia się do precyzyjnych wyliczeń.

Aby prawidłowo zastosować ten wzór, musisz dysponować:

długościami obu przekątnych,
wartością kąta γ,
przydatnością w sytuacji, gdy kąt między przekątnymi nie jest prosty.

W praktyce wzór ten staje się niezwykle użyteczny, gdy inne wymiary równoległoboku są nieznane. Co więcej, dzięki nowoczesnym narzędziom matematycznym i kalkulatorom online, obliczanie pola równoległoboku przy użyciu tego wzoru stało się dużo łatwiejsze.

Jak obliczyć pole równoległoboku w praktyce?

Obliczanie pola równoległoboku wiąże się z koniecznością znajomości określonych wartości geometrycznych oraz odpowiednich wzorów matematycznych. Istnieją trzy podstawowe podejścia, które można zastosować do tego zadania, a każde z nich sprawdzi się w różnych okolicznościach.

pierwsza metoda opiera się na wzorze P = a × h, gdzie a to długość podstawy, a h oznacza wysokość równoległoboku,
kiedy dysponujemy długościami dwóch boków oraz kątem między nimi, możemy wykorzystać wzór P = a × b × sin α, gdzie a i b oznaczają długości boków, a α to kąt, który je łączy,
alternatywnie, gdy mamy do czynienia z długościami przekątnych oraz kątem pomiędzy nimi, możemy użyć wzoru P = 1/2 × d₁ × d₂ × sin γ, gdzie d₁ i d₂ to długości przekątnych, a γ to łączący je kąt.

W praktycznym zastosowaniu kluczowe jest umiejętne rozpoznanie dostępnych parametrów. Dzięki temu można wybrać najodpowiedniejszą metodę obliczeń. Poprawne stosowanie wzorów gwarantuje dokładne i efektywne wyznaczenie pola równoległoboku.

Obliczanie pola z podstawy i wysokości

Obliczanie powierzchni równoległoboku na podstawie długości jego podstawy oraz wysokości to kluczowa umiejętność w geometrii. Do obliczeń wystarczy skorzystać z prostego wzoru: P = a × h, gdzie P oznacza pole powierzchni, a to długość podstawy, a h to wysokość, która jest opuszczona na tę podstawę.

Wysokość to prostopadła odległość mierzona od podstawy do napotkanego boku równoległoboku. Aby dokładnie określić pole, najpierw zmierz długość podstawy, a następnie jej wysokość. Na przykład, jeśli podstawa ma 5 cm, a wysokość wynosi 4 cm, to wynik obliczeń będzie wynosić 20 cm² (5 cm × 4 cm).

Ta technika jest bardzo intuicyjna, zwłaszcza gdy wszystkie niezbędne dane są pod ręką. Dodatkowo, znajduje zastosowanie w wielu dziedzinach, takich jak:

architektura,
inżynieria,
nauka matematyczna.

Obliczanie pola z długości boków i kąta

Aby znaleźć pole równoległoboku, wystarczy skorzystać z prostego równania: P = a × b × sin α. W tym równaniu ’a’ i ’b’ to długości boków leżących obok siebie, a ’α’ to kąt, jaki między nimi tworzą. Najważniejszą częścią wzoru jest sinus kąta, który obrazuje, w jaki sposób te boki są względem siebie ustawione.

Taka metoda obliczeń jest niezwykle przydatna, zwłaszcza gdy nie dysponujemy wysokością równoległoboku, ale znamy długości boków oraz miarę kąta. Weźmy na przykład sytuację, gdy mamy boki o długości 5 cm i 8 cm, a kąt α wynosi 30°. Obliczenie pola równoległoboku zrealizujemy w kilku prostych krokach:

Najpierw obliczamy sinus kąta: sin 30° = 0,5,
Następnie podstawiamy wartości do równania: P = 5 cm × 8 cm × 0,5,
Ostatecznie uzyskujemy wynik: P = 20 cm².

Dzięki tej metodzie obliczanie pola równoległoboku staje się zarówno łatwe, jak i efektywne, szczególnie w sytuacjach, gdy brakuje innych danych. Zrozumienie tego wzoru może okazać się bardzo pomocne w różnych dziedzinach, takich jak matematyka, architektura czy inżynieria.

Obliczanie pola z przekątnych i kąta między nimi

Aby znaleźć pole powierzchni równoległoboku, potrzebujemy znać długości jego przekątnych oraz kąt, który znajduje się między nimi. Możemy skorzystać z odpowiedniego wzoru:

P = 1/2 × d₁ × d₂ × sin(γ)

W tym równaniu d₁ i d₂ oznaczają długości przekątnych, a γ to kąt, który je łączy. Wiedza na temat wartości funkcji sinus dla kąta γ ma ogromne znaczenie, gdyż wpływa na dokładność naszych obliczeń.

W przypadku prostokątów i kwadratów pomiar długości boków oraz wysokości jest stosunkowo prosty. Natomiast przy równoległobokach uzyskanie wysokości bywa bardziej złożone. Dlatego często bardziej praktyczne staje się skupienie na kącie oraz długościach przekątnych.

Na przykład, jeśli przekątne równoległoboku mierzą 10 cm i 8 cm, a kąt między nimi wynosi 30 stopni, obliczenia pola mogą wyglądać tak:

P = 1/2 × 10 cm × 8 cm × sin(30°) = 1/2 × 10 × 8 × 0.5 = 20 cm².

Taka metoda obliczania pola jest nie tylko skuteczna, ale również praktyczna. Szczególnie przydaje się w sytuacjach, kiedy łatwiej jest zmierzyć długości przekątnych niż wysokość.

Kiedy stosuje się poszczególne wzory na pole równoległoboku?

Wybór właściwego wzoru do obliczania pola równoległoboku zależy od dostępnych informacji. Istnieją trzy podstawowe sposoby, które można zastosować w różnych sytuacjach:

P = a × h – gdy znamy długości podstawy oraz wysokości,
P = a × b × sin α – gdy dysponujemy długościami obu boków oraz kątem, który je łączy,
P = 1/2 × d₁ × d₂ × sin γ – gdy znamy przekątne oraz kąt pomiędzy nimi.

Pierwsza metoda polega na wykorzystaniu wzoru, gdy znamy długości podstawy oraz wysokości. To najprostsza i najczęściej stosowana technika, która doskonale sprawdza się w sytuacjach, w których wysokość można łatwo zmierzyć.

Druga metoda jest przydatna, gdy nie mamy dostępu do wysokości, co często ma miejsce w praktyce inżynieryjnej, gdzie regularnie obliczamy różne kąty i długości.

Trzecia technika jest nieco bardziej złożona, ale stosuje się ją doskonale w geometrii analitycznej.

Każda z tych metod zapewnia elastyczność przy obliczeniach oraz umożliwia precyzyjne dostosowanie do konkretnych warunków. Właściwy wybór wzoru ma ogromny wpływ na efektywność obliczeń i dokładność uzyskiwanych wyników.

Metody wyboru odpowiedniego wzoru

Wybór odpowiedniego wzoru do obliczenia pola równoległoboku odgrywa istotną rolę w uzyskiwaniu precyzyjnych danych. Istnieją trzy główne podejścia, które mogą być użyte, w zależności od posiadanych informacji geometrycznych:

pierwsza z metod polega na znajomości wysokości oraz długości podstawy. W tym przypadku najczęściej sięga się po wzór P = a × h, gdzie „a” reprezentuje długość podstawy, a „h” jest wysokością,
drugą opcją jest wykorzystanie długości boków oraz kąta między nimi. Gdy te dane są dostępne, stosujemy wzór P = a × b × sin α, gdzie „a” i „b” to długości boków, natomiast „α” to kąt, który je łączy,
trzeci sposób odnosi się do sytuacji, gdy znamy długości obu przekątnych oraz kąt, jaki między nimi występuje. Wówczas korzystamy ze wzoru P = 1/2 × d₁ × d₂ × sin γ, gdzie „d₁” i „d₂” oznaczają długości przekątnych, a „γ” to kąt między nimi.

Umiejętność dobrego dobrania metody w odpowiedniej sytuacji znacznie zwiększa efektywność obliczeń, co pozwala na uzyskanie dokładnych wyników.

Które dane są potrzebne?

Aby obliczyć pole równoległoboku, musimy posłużyć się różnymi danymi, zależnie od wybranego wzoru.

Oto różne wzory do obliczania pola równoległoboku:

wzór P = a × h: potrzebujemy długości podstawy (a) oraz wysokości (h) równoległoboku,
wzór P = a × b × sin α: konieczne będą długości dwóch sąsiadujących boków (a i b) oraz miara kąta (α) leżącego między nimi,
wzór P = 1/2 × d₁ × d₂ × sin γ: musimy znać długości przekątnych (d₁ i d₂) oraz kąt (γ) między nimi.

Zrozumienie tych parametrów jest kluczowe, aby precyzyjnie obliczyć powierzchnię równoległoboku.

Jakie są znaczenia parametrów w wzorach na pole równoległoboku?

Parametry we wzorach dotyczących pola równoległoboku odgrywają niezwykle istotną rolę w geometrii. Długości boków, w tym podstawy, definiują rozmiary tej figury. Z kolei wysokość to odległość prostopadła pomiędzy podstawą a przeciwległym bokiem, co jest kluczowe dla obliczenia pola. Kąt utworzony między bokami, a także przekątnymi, także wpływa na te wyliczenia, wykorzystując funkcję sinus. Przykładowo, w równaniu P = a × b × sin α kąt α ma zasadnicze znaczenie dla określenia powierzchni.

Nie mniej ważne są długości przekątnych. W innym wzorze, P = 1/2 × d₁ × d₂ × sin γ, γ oznacza kąt powstały między przekątnymi. Kluczowe jest zrozumienie wszystkich tych parametrów, aby prawidłowo obliczyć pole równoległoboku oraz móc skutecznie interpretować wyniki. Każdy z tych aspektów – od długości boków, przez wysokość, po kąty – ma znaczenie w analizie geometrii równoległoboku.

Długości boków i podstawy

Długości boków równoległoboku mają ogromne znaczenie w matematyce, zwłaszcza przy obliczaniu pola tej figury. Kluczowa tu jest długość podstawy, na którą działa wysokość. Inne boki również wpływają na kształt kątów, tworząc specyfikę równoległoboku, składającego się z dwóch par równoległych boków. Z tego względu długości boków oraz podstawy są niezbędne podczas wszystkich obliczeń.

Jeśli chodzi o obliczanie pola równoległoboku, istnieje kilka użytecznych wzorów bazujących na długości boków oraz podstawie:

za pomocą wzoru P = a × h, długość podstawy (a) w połączeniu z wysokością (h) są kluczowe,
inny, bardziej zaawansowany wzór, P = a × b × sin α, uwzględnia długości boków a oraz b oraz kąt α, co również wpływa na wynik.

Długości boków równoległoboku kształtują jego formę oraz charakterystyki. Wiedza dotycząca tych wartości umożliwia nie tylko obliczenie pola, ale także lepsze zrozumienie geometrii równoległoboku w porównaniu do innych figur płaskich, takich jak prostokąty czy trapezy.

Umiejętność obliczania długości boków oraz podstawy równoległoboku jest niezbędna w różnych dziedzinach, takich jak:

architektura,
geometria,
geodezja.

Co więcej, te umiejętności mają fundamentalne znaczenie w edukacji matematycznej, gdzie uczniowie poznają te zagadnienia poprzez praktyczne ćwiczenia.

Wysokość odpowiadająca podstawie

Wysokość równoległoboku to niezwykle istotny parametr kluczowy w obliczeniach jego pola. Można ją zdefiniować jako prostopadłą odległość pomiędzy podstawą a przeciwległym bokiem. Aby obliczenia były prawidłowe, należy pamiętać, że wysokość musi odpowiadać wybranej podstawie, inaczej wyniki mogą okazać się błędne.

Do obliczenia pola równoległoboku posługujemy się prostą formułą:

P = a × h, gdzie „a” oznacza długość podstawy,
„h” to wysokość.

Precyzyjne ustalenie wartości wysokości jest niezastąpione, zwłaszcza w takich dziedzinach jak architektura czy inżynieria, gdzie niewłaściwe dane mogą prowadzić do poważnych konsekwencji.

Na przykład, rozważmy równoległobok o podstawie długości 5 cm oraz wysokości równającej się 3 cm. W takim przypadku pole wyniesie 15 cm². To doskonały przykład na to, jak ważne jest precyzyjne dopasowanie wysokości do podstawy przy obliczaniu pola równoległoboku.

Kąt i sinus kąta

Kąt oraz wartość funkcji sinus są niezbędne przy wyznaczaniu pola równoległoboku. Kąt (α), leżący pomiędzy dwoma sąsiednimi bokami, oraz kąt (γ) stworzony przez przekątne odgrywają kluczową rolę w tych obliczeniach. Dzięki wykorzystaniu wzorów trygonometrycznych możemy dokładnie określić powierzchnię równoległoboku. Wartość kąta wpływa bezpośrednio na obliczenia, a sinus kąta (sin α) ujawnia, jak strome są boki czy przekątne.

Możemy zapisać wzór na pole równoległoboku w postaci P = b × h, gdzie b oznacza długość podstawy, a h to wysokość. Innym sposobem na obliczenie pola jest użycie formuły P = a × b × sin α, która uwzględnia sinus kąta. Przy tym wzorze niezwykle istotne jest zrozumienie wpływu kąta na wyniki. Im większy kąt, tym wyższa wartość sin α, co prowadzi do większego obszaru równoległoboku.

Kiedy analizujemy kąt między przekątnymi, warto umieścić go w szerszym kontekście geometrii i konstrukcji. Sinus kąta (sin γ) także znajdzie zastosowanie w odpowiednich formułach do precyzyjnego wyznaczania pola. Dlatego umiejętność prawidłowego obliczania kątów jest kluczowa dla dokładności wszelkich analiz.

Stosując te zasady, możemy skutecznie wykorzystać trygonometrię w obliczeniach dotyczących geometrii. To podkreśla znaczenie kąta i jego funkcji sinus w kontekście równoległoboku.

Długości przekątnych

Przekątne równoległoboku stanowią istotny element tej figury, łącząc przeciwległe wierzchołki. Długości tych przekątnych, określanych jako d₁ i d₂, są kluczowe przy obliczaniu pola. Istnieją różne sposoby na ich wyznaczenie – można posłużyć się nie tylko długością podstawy i wysokością, lecz także formułą P = 1/2 × d₁ × d₂ × sin γ, gdzie γ to kąt pomiędzy przekątnymi.

Często długości przekątnych są różne, chyba że mamy do czynienia z rombem, w którym są one równe. Każda z tych długości ma wpływ na pole, które równoległobok może objąć. Przekątne w tej figurze przecinają się w swoim środku, dzieląc ją na dwa mniejsze równoległoboki. Wartość kąta γ jest istotna, ponieważ jego miara oddziałuje na sinus, co bezpośrednio wpływa na obliczenia pola.

Zrozumienie długości przekątnych oraz odpowiedniego kąta umożliwia skuteczne zastosowanie wspomnianego wzoru. W ten sposób staje się on niezwykle pomocnym narzędziem w dziedzinie matematyki przestrzennej i geometrii.

Jak przekształcić wzór na pole równoległoboku?

Aby zrozumieć, jak przekształcić wzór na pole równoległoboku, warto przyjrzeć się kluczowym elementom tego działania. Najpopularniejszy wzór to P = a × h, gdzie a oznacza długość podstawy, a h to wysokość. Można go dostosować, aby obliczyć różne parametry.

Na przykład, co zrobić, gdy wysokość h jest nam nieznana? W takiej sytuacji można zastosować wzór trygonometryczny P = a × b × sin α. Tutaj b to długość drugiej podstawy, a α to kąt między podstawami. Modyfikując ten wzór, możemy wyznaczyć długość podstawy, dysponując wartością pola i wysokości.

Istnieją również inne metody przekształceń. Na przykład, wykorzystując wzór P = (1/2) × d₁ × d₂ × sin γ, gdzie d₁ i d₂ to długości przekątnych równoległoboku, możemy z łatwością obliczyć różne niewiadome, pod warunkiem, że mamy pozostałe wartości.

Takie przekształcenia wzorów są niezwykle przydatne w różnych obszarach matematyki. Umożliwiają nam dostosowanie metod obliczeniowych do posiadanych danych. Zrozumienie, jak znaleźć odpowiedni wzór i go przekształcić, to kluczowe elementy skutecznych obliczeń geometrycznych.

Przykłady obliczeń pola równoległoboku

Przykłady obliczeń pola równoległoboku stanowią ważny element nauki matematyki. Umożliwiają one praktyczne zastosowanie różnych wzorów do realnych sytuacji. W przypadku zadań geometrycznych kluczowe jest, aby zrozumieć, w jaki sposób używać formuł do wyznaczania pola równoległoboku.

Rozpocznijmy od pierwszego przykładu, gdzie posłużymy się wzorem P = a × h. Załóżmy, że podstawa równoległoboku wynosi 6 cm, a jego wysokość to 4 cm. W takim razie pole możemy obliczyć tak: P = 6 cm × 4 cm, co daje nam 24 cm².

W drugim przypadku skorzystamy z formuły P = a × b × sin α. Przyjmujemy, że długości boków to 5 cm i 7 cm, a kąt α ma wartość 30 stopni. Wówczas pole obliczamy następująco: P = 5 cm × 7 cm × sin(30°) = 5 cm × 7 cm × 0.5, co daje 17.5 cm².

Trzeci przykład z kolei ilustruje wzór P = 1/2 × d₁ × d₂ × sin γ. Dłuższe przekątne równoległoboku mają długości 8 cm i 10 cm, a kąt γ wynosi 60 stopni. Przy obliczeniach otrzymujemy: P = 1/2 × 8 cm × 10 cm × sin(60°) = 1/2 × 8 cm × 10 cm × √3/2. Wynik to 20√3 cm², co daje w przybliżeniu około 34.64 cm².

Prezentowane przykłady pokazują różnorodne metody obliczania pola równoległoboku. Ilustrują one praktyczne zastosowanie tych formuł, co jest niezwykle ważne w kontekście rozwiązywania zadań oraz ćwiczeń związanych z geometrią.

Przykład z wysokością

Przykład dotyczący wysokości doskonale ilustruje, jak można obliczyć pole równoległoboku, znając długość jego podstawy oraz wysokość. Wystarczy skorzystać z prostego wzoru: P = a × h, gdzie P oznacza pole, „a” to długość podstawy, a „h” to wysokość opuszczona prostopadle na tę podstawę. Dzięki temu wzorowi obliczenia stają się szybkie i łatwe.

Rozważmy konkretne liczby:

jeśli długość podstawy wynosi 5 cm,
a wysokość to 4 cm,
pole obliczamy tak: P = 5 cm × 4 cm = 20 cm².

Taki łatwy sposób liczenia ma ogromne znaczenie w praktyce, na przykład w branży budowlanej czy w projektowaniu. Nic więc dziwnego, że zagadnienia związane z wysokością pojawiają się w zadaniach matematycznych oraz podczas nauki geometrii.

Przykład z bokami i kątem

Przykład dotyczący boków i kąta doskonale ilustruje, w jaki sposób można obliczyć pole równoległoboku, znając długości dwóch sąsiednich boków oraz kąt między nimi. Używamy w tym celu wzoru P = a × b × sin α.

W tym wzorze:

a oznacza długość jednego z boków,
b to długość drugiego boku,
α to kąt utworzony pomiędzy tymi bokami.

Kluczowe jest to, że wzór ten uwzględnia wpływ kąta na pole powierzchni, co jest szczególnie ważne, gdy boki nachylają się względem siebie.

Aby lepiej zobrazować proces obliczeń, rozważmy konkretny przykład. Przyjmijmy, że długości boków wynoszą odpowiednio 5 cm i 8 cm, a kąt między nimi ma wartość 30 stopni.

Najpierw obliczamy sinus kąta: sin 30° = 0,5.
Następnie wprowadzamy wartości do wzoru: P = 5 cm × 8 cm × 0,5, co daje nam 20 cm².

Ostatecznie obliczone pole równoległoboku wynosi 20 cm². Tako informacje są pomocne w zrozumieniu, w jaki sposób różne parametry wpływają na wyniki w geometrii.

Przykład z przekątnymi

Aby określić pole równoległoboku na podstawie długości jego przekątnych, można skorzystać z następującego wzoru:

P = 1/2 × d₁ × d₂ × sin γ

W tym równaniu d₁ oraz d₂ reprezentują długości przekątnych, a γ to kąt, który je łączy. Jest niezwykle istotne, aby zwrócić uwagę na wartość kąta, ponieważ sinus kąta ma istotny wpływ na ostateczny rezultat.

Weźmy na przykład równoległobok, w którym długości przekątnych wynoszą 6 cm i 8 cm, a kąt między nimi to 30°.

Najpierw musimy obliczyć sinus kąta 30°, który wynosi 0,5. Następnie wprowadzamy nasze pomiary do wzoru:

P = 1/2 × 6 × 8 × sin 30° = 1/2 × 6 × 8 × 0,5 = 12 cm².

Ten przykład doskonale ilustruje, jak długości przekątnych i kąt między nimi wpływają na pole równoległoboku. Aby uzyskać prawidłowy wynik, warto znać zarówno długości przekątnych, jak i kąt.

Jak pole równoległoboku odnosi się do innych figur płaskich?

Pole równoległoboku jest ściśle związane z obliczeniami dotyczącymi innych figur płaskich, co wpływa na korzystanie z różnych wzorów oraz logiczne wnioskowanie w geometrii. Romb, będący szczególną odmianą równoległoboku, wyróżnia się tym, że wszystkie jego boki mają jednakową długość. Istnieją dwa sposoby na obliczenie jego pola:

korzystając z połowy iloczynu długości przekątnych,
poprzez pomnożenie długości boku przez odpowiadającą mu wysokość.

Warto zauważyć, że porównując równoległobok z prostokątem, stwierdzamy, iż pole obu figur jest takie samo, o ile mają identyczne wymiary podstawy oraz wysokości. Dzięki temu, po dokonaniu pomiarów, łatwo jest zestawić te wartości ze sobą, co ułatwia zrozumienie tej relacji.

W przypadku trapezu równoległobok wyróżnia się posiadaniem dwóch par równoległych boków. Ta cecha czyni obliczenia prostszymi, ponieważ możemy z łatwością zastosować wzory związane z polem prostokąta oraz równoległoboku, bez obaw o różnice w długości boków. Z kolei trapez oferuje wiele metod obliczania pola, które mogą się różnić w zależności od dostępnych informacji.

Długości boków, przekątne i wysokość równoległoboku odgrywają kluczową rolę w obliczeniach. Zrozumienie tych powiązań znacząco ułatwia rozwiązywanie różnych zadań geometrycznych, zwłaszcza związanych z figurami płaskimi. Analizując te relacje, zdobywamy cenne informacje, które ukazują znaczenie równoległoboków w geometrii.

Pole rombu jako szczególny przypadek

Obliczanie pola rombu, który jest szczególnym przypadkiem równoległoboku, można łatwo przeprowadzić za pomocą wzorów stworzonych dla równoległoboków, z uwzględnieniem jego unikalnych cech. Ta figura charakteryzuje się tym, że wszystkie boki mają jednakową długość, co znacząco upraszcza obliczenia.

Aby obliczyć pole rombu, można skorzystać z formuły P = a × h, gdzie „a” to długość boku, a „h” to wysokość względem tej podstawy. Alternatywnie, jeśli posiadamy długości przekątnych, możemy zastosować wzór P = 1/2 × d₁ × d₂, w którym d₁ i d₂ oznaczają długości odpowiednich przekątnych. Dzięki tym właściwościom romb staje się prostą do analizy figurą w kontekście równoległoboków, co okazuje się nieocenione w rozwiązywaniu zadań i problemów geometrycznych.

Znajomość wzorów oraz metod obliczania pola rombu nie tylko przyspiesza proces rozwiązywania standardowych zadań, ale także pomaga w lepszym rozumieniu relacji między rombem a innymi figurami płaskimi. Kiedy pracujemy z równoległobokami i rombami, kluczowe jest precyzyjne określenie długości boków, odpowiednich wysokości oraz umiejętność mierzenia przekątnych.

Porównanie z polem prostokąta i trapezu

Równoległobok, prostokąt i trapez różnią się nie tylko swoją formą, ale także metodami obliczania ich pola powierzchni. W przypadku równoległoboku pole jest równoznaczne z polem prostokąta, jeśli oba mają te same długości podstawy i wysokości. Można to doskonale zobrazować, wyobrażając sobie przekształcenie równoległoboku w prostokąt. Na przykład, przy podstawie równoległoboku wynoszącej 5 cm i wysokości 3 cm, obliczone pole wynosi 15 cm². To ta sama wartość, która uzyskana byłaby dla prostokąta o identycznych wymiarach.

Z kolei trapez stawia przed nami nieco inne wyzwania. Jego charakterystyczną cechą jest posiadanie tylko jednej pary boków równoległych, co wprowadza bardziej skomplikowany wzór do obliczeń: P = (a + b) × h / 2. W tym równaniu „a” i „b” reprezentują długości podstaw, a „h” to wysokość. Umiejętność korzystania z tych wzorów ma kluczowe znaczenie nie tylko w matematyce, ale również w takich dziedzinach jak architektura czy inżynieria.

Zrozumienie różnic między tymi figurami geometrycznymi jest niezwykle istotne. Ta wiedza znajduje zastosowanie w różnych sytuacjach. Na przykład, w geometrii równoległobok może być użyteczny podczas obliczania większych powierzchni, natomiast trapez sprawdza się znakomicie przy studiowaniu powierzchni o określonym nachyleniu.

W jakich dziedzinach wykorzystuje się obliczanie pola równoległoboku?

Obliczanie pola równoległoboku ma wiele praktycznych zastosowań, co czyni je cennym narzędziem w różnych dziedzinach.

W architekturze oraz inżynierii zdolność do ustalania powierzchni równoległoboków jest niezwykle istotna. Te umiejętności pozwalają na dokładne określenie powierzchni elementów konstrukcyjnych, co z kolei wpływa na projektowanie budynków i innych obiektów inżynieryjnych. Dzięki precyzyjnym obliczeniom można efektywnie zaplanować, jakie materiały będą potrzebne do realizacji projektów oraz lepiej wykorzystać dostępną przestrzeń.

Również w geodezji pole równoległoboku odgrywa kluczową rolę. Stosuje się je do dokładnych pomiarów terenowych oraz mapowania. Dzięki obliczeniom geometrycznym można precyzyjnie ustalić wielkość poszczególnych obszarów, co jest niezbędne w planowaniu przestrzennym i zarządzaniu gruntami.

Edukacja matematyczna również czerpie korzyści z tego zagadnienia. Obliczanie pola równoległoboku stanowi fundament geometrii, umożliwiając uczniom rozwiązywanie różnorodnych zadań. Tego rodzaju ćwiczenia rozwijają ich myślenie analityczne oraz logiczne umiejętności.

Warto podkreślić, że umiejętność obliczania pola równoległoboku ma znaczenie zarówno w:

architekturze,
inżynierii,
geodezji,
edukacji matematycznej.
a jej zastosowanie ma zasadniczy wpływ na wiele aspektów życia codziennego.

Architektura i inżynieria

W architekturze i inżynierii obliczenie pola równoległoboku odgrywa kluczową rolę w projektowaniu oraz analizowaniu powierzchni różnorodnych elementów budowlanych, takich jak dachy, ściany czy podłogi. Architekci muszą precyzyjnie określić wymiary, aby odpowiednio dobrać materiały i zapewnić stabilność całej konstrukcji.

Znajomość wzorów na pole równoległoboku, takich jak P = a × h, pozwala na szybkie i trafne obliczenia, co jest niezwykle istotne w fazie planowania. Na przykład podczas projektowania dachu o kształcie równoległoboku, architekt wykorzysta te wyliczenia do oszacowania potrzebnej ilości materiałów do pokrycia.

W inżynierii lądowej obliczenia pola równoległoboku są niezbędne do analizy układów przestrzennych, w których występują elementy o kształcie równoległoboków. Tego typu obliczenia mają także zastosowanie w analizie obciążenia konstrukcji, co jest kluczowe dla zapewnienia ich bezpieczeństwa.

Dla geodetów precyzyjne wyliczanie pól równoległoboków ułatwia określenie granic działek oraz projektowanie przestrzeni. Zrozumienie tych wzorów jest również ważne w kontekście edukacji matematycznej, gdzie uczniowie uczą się ich zastosowania poprzez różnorodne zadania i ćwiczenia.

Obliczanie pola równoległoboku ma zatem istotne znaczenie w architekturze i inżynierii, a jego praktyczne zastosowanie znajdują w różnych aspektach projektowania oraz analizy konstrukcji.

Geodezja

Geodezja to fascynująca dziedzina, która wykorzystuje różnorodne techniki obliczania pól równoległoboków w licznych zastosowaniach terenowych. Takie obliczenia odgrywają kluczową rolę w pomiarach, które pozwalają na precyzyjne określenie powierzchni działek oraz projektowanie map. Dzięki odpowiednim wzorom możliwe jest błyskawiczne i dokładne ustalenie powierzchni na podstawie zmierzonych długości boków oraz kątów.

W praktyce geodezyjnej obliczenia powierzchni często opierają się na danym zbiorze pomiarów, takich jak:

długości boków,
wysokości.

To z kolei ułatwia efektywne planowanie przestrzenne. Zastosowanie konkretnych formuł pozwala geodetom z dużą precyzją wyznaczać powierzchnię dla różnych form terenu. W przypadku, gdy dostępne są podstawy i wysokości lub długości przekątnych oraz kąty, takie wzory jak:

P = a × h,
P = 1/2 × d₁ × d₂ × sin γ stają się niezwykle użyteczne.

Znajomość tych formuł jest kluczowa w codziennej pracy geodetów, pozwalając na lepsze zrozumienie złożoności obliczeń dotyczących różnorodnych kształtów. Wiele osób w tej profesji korzysta z tych zasad regularnie, aby zapewnić dokładność wyników pomiarów oraz analiz. Ponadto, tego rodzaju obliczenia mają istotne znaczenie w kontekście rozwoju infrastrukturalnego, co wspiera efektywniejsze planowanie projektów budowlanych oraz zarządzanie terenami.

Edukacja matematyczna i zadania szkolne

Edukacja matematyczna dotycząca obliczania pola równoległoboku ma kluczowe znaczenie w nauce geometrii. Angażuje uczniów, pozwala im zgłębiać właściwości figur płaskich oraz rozwija umiejętności niezbędne do zrozumienia tej dziedziny. Lekcje matematyki obejmują różnorodne zadania i ćwiczenia, które nie tylko rozwijają umiejętności obliczeniowe, ale również promują praktyczne stosowanie wzorów.

Na przykład, uczniowie poznają, jak obliczać pole równoległoboku za pomocą formuł takich jak P = a × h oraz P = a × b × sin α. Dzięki temu zdobywają zarówno teoretyczną wiedzę, jak i praktyczne umiejętności, które mogą wykorzystać w różnych sytuacjach.

Interaktywne ćwiczenia oraz codzienne przykłady znacząco ułatwiają proces nauczania, sprawiając, że uczniowie lepiej dostrzegają, jak geometria oddziałuje na ich otoczenie. Zrozumienie obliczania pola równoległoboku wykracza poza teoretyczne rozważania – to przydatna umiejętność, która może okazać się wartościowa w przyszłej karierze. Edukacja matematyczna dostarcza niezbędnych narzędzi, umożliwiając skuteczne rozwiązywanie problemów geometrycznych i obliczeniowych.

Jakie są jednostki pola równoległoboku?

Jednostki pola równoległoboku odnoszą się do sposobów wyrażania powierzchni, które obliczamy. Najpopularniejsze z nich to:

metry kwadratowe (m²),
centymetry kwadratowe (cm²),
milimetry kwadratowe (mm²).

Kiedy zaczynamy liczyć powierzchnię równoległoboku, ważne jest, aby pamiętać, że wynik będzie zależał od jednostek długości, które wykorzystamy do zmierzenia boków, wysokości lub przekątnych figury.

Aby uzyskać precyzyjne wyniki, konieczne jest utrzymanie spójności jednostek długości. Przykładowo, jeśli zmierzymy boki równoległoboku w centymetrach, to pole musi być wyrażone w centymetrach kwadratowych. Warto również zauważyć, że w różnych kontekstach, takich jak lokalizacja geograficzna czy branża, mogą być używane inne jednostki, na przykład cale kwadratowe lub stopy kwadratowe.

Zrozumienie tych jednostek jest niezwykle istotne, szczególnie w profesjach takich jak architektura, inżynieria czy geodezja. W tych dziedzinach precyzyjne obliczenia są kluczowe dla opracowywania dokładnych planów oraz analiz.

Czy istnieją narzędzia do automatycznego obliczania pola równoległoboku?

W dzisiejszych czasach dostępnych jest wiele nowoczesnych narzędzi, które znacznie ułatwiają obliczanie pola równoległoboku. Na przykład, popularne kalkulatory online, takie jak kalkulator pola równoległoboku, pozwalają na szybkie i precyzyjne wyliczenia po wprowadzeniu odpowiednich danych. Wystarczy wskazać długość podstawy oraz wysokość, a wynik pojawi się błyskawicznie.

Dodatkowo, wykorzystanie animacji i interaktywnych ćwiczeń może znacząco wzbogacić proces nauki matematyki. Pomagają one w lepszym zrozumieniu zasad dotyczących pola równoległoboku, pozwalając uczniom na praktyczne zastosowanie wzorów w angażujący sposób. Tego rodzaju narzędzia okazują się niezwykle przydatne zarówno w szkołach, jak i w czasie nauki samodzielnej, sprzyjając efektywniejszemu przyswajaniu wiedzy oraz rozwijaniu kluczowych umiejętności.

Kalkulator online

Kalkulator online to niezwykle przydatne narzędzie, które szybko oblicza pole równoległoboku. Wystarczy wpisać długości boków, wysokość, kąt lub długości przekątnych, a kalkulator samodzielnie stosuje odpowiednie wzory, by uzyskać wynik. Dzięki temu proces obliczania staje się prostszy, eliminując konieczność wykonywania skomplikowanych obliczeń ręcznych.

To narzędzie znajduje zastosowanie w wielu dziedzinach, takich jak:

architektura,
inżynieria,
matematyka edukacyjna.

Ułatwia zrozumienie metod obliczeniowych oraz umożliwia szybkie porównywanie rezultatów. Użytkownicy mogą wybierać spośród różnych metod, co sprawia, że nauka oraz praca stają się bardziej efektywne.

W kontekście edukacji, kalkulator online zyskuje szczególne uznanie, ponieważ interaktywne podejście do matematyki znacząco ułatwia przyswajanie zagadnień geometrycznych. To narzędzie nie tylko pozwala zaoszczędzić czas, ale także zmniejsza ryzyko popełnienia błędów w obliczeniach, co ma fundamentalne znaczenie w pracy zawodowej i badawczej.

Animacje i ćwiczenia interaktywne

Animacje i interaktywne ćwiczenia odgrywają kluczową rolę w nauczaniu matematyki, zwłaszcza gdy mówimy o równoległobokach. Umożliwiają uczniom lepsze zrozumienie i wizualizację właściwości tej figury geometrycznej. Dzięki takim narzędziom łatwiej jest dostrzegać skomplikowane zależności między jej elementami, takimi jak: boki, kąty oraz przekątne.

Interaktywne zadania dają okazję do praktycznego zastosowania wzorów na pole równoległoboku, co znacznie podnosi umiejętności obliczeniowe uczniów. Na przykład, mogą oni:

zmieniać długości boków,
zmieniać wysokość figury,
obserwować wpływ modyfikacji na wartość pola.

Takie zajęcia są nie tylko ciekawsze, ale też bardziej efektywne w procesie edukacji.

Dzięki animacjom uczniowie mogą zobaczyć w akcji różne wzory na pole, takie jak:

P = a × h,
P = a × b × sin α,
P = 1/2 × d₁ × d₂ × sin γ.

Wizualizacje dostarczają klarownych przykładów, zachęcając do odkrywania matematyki w sposób interaktywny oraz wizualny.

Co więcej, korzystanie z narzędzi interaktywnych sprzyja współpracy w grupach oraz ułatwia prowadzenie dyskusji. Taki sposób nauki sprawia, że matematyka staje się bardziej dynamiczna i lepiej dostosowuje się do indywidualnych potrzeb uczniów. Mają oni możliwość ćwiczenia w pojedynkę, jednocześnie korzystając z wsparcia nauczycieli, co przyspiesza przyswajanie wiedzy o obliczaniu pola równoległoboku.