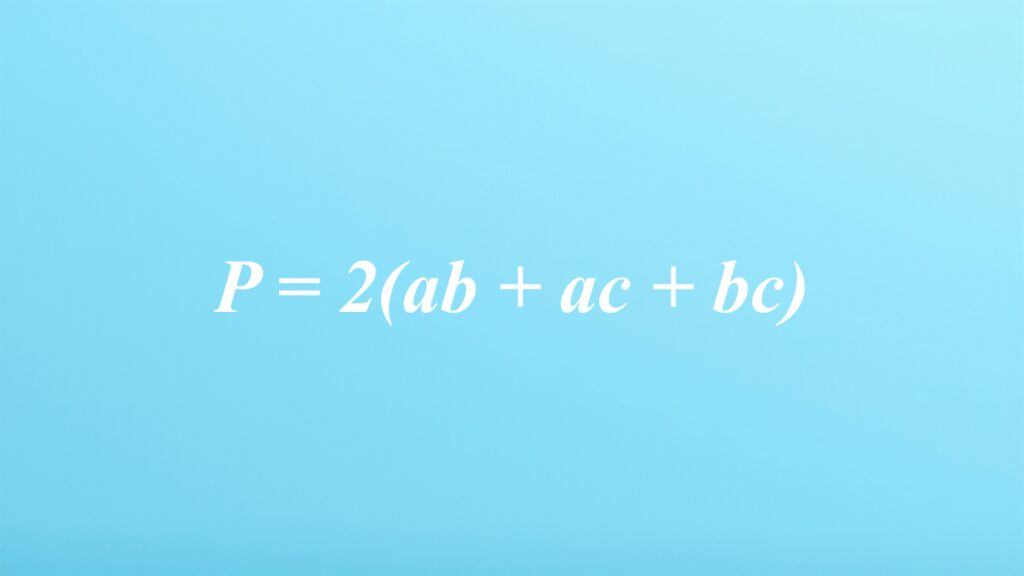Wzór na pole prostopadłościanu

Czym jest prostopadłościan i jakie ma właściwości?

Prostopadłościan to figura przestrzenna składająca się z sześciu prostokątnych ścian. Dwie z tych ścian pełnią funkcję podstaw, podczas gdy pozostałe cztery to ściany boczne. To ważny kształt w geometrii, który stanowi fundament dla wielu teorii matematycznych. Wymiary prostopadłościanu, takie jak długość, szerokość i wysokość, pozwalają precyzyjnie określić jego kształt oraz wielkość.

Ciekawą cechą prostopadłościanu są trzy pary przeciwległych ścian, które mają jednakowe wymiary i powierzchnie. Warto także wspomnieć, że sześcian, jako szczególny przypadek prostopadłościanu, charakteryzuje się równymi krawędziami. Prostopadłościan odgrywa znaczącą rolę w wielu dziedzinach, takich jak:

• inżynieria,
• architektura,
• nauki przyrodnicze.
• zastosowania praktyczne.

Ze względu na swoje właściwości, prostopadłościan umożliwia nie tylko badanie podstawowych relacji geometrycznych, ale także jest istotny w rozmaitych zastosowaniach praktycznych. Przykładowo, jest często wykorzystywany do obliczania objętości i powierzchni w kontekście budowlanym oraz projektowym.

Jakie są ściany i wymiary prostopadłościanu?

Prostopadłościan to figura geometryczna składająca się z sześciu prostokątnych ścian, które tworzą trzy pary o identycznych wymiarach i polach. Wymiary tego obiektu definiujemy trzema wartościami: długością (a), szerokością (b) oraz wysokością (h). Te pomiary są kluczowe dla obliczeń dotyczących jego powierzchni i objętości.

Krawędzie prostopadłościanu są ściśle powiązane z wymienionymi wymiarami. Można to streścić w następujący sposób:

• krawędzi poziome odpowiadają długości oraz szerokości,
• krawędzi pionowe związane są z jego wysokością.

Zastosowanie ścian prostopadłościanu jest szerokie, od budownictwa po projektowanie. Dlatego znajomość jego wymiarów jest niezbędna do dalszych obliczeń dotyczących powierzchni i objętości tej geometrycznej bryły.

Dlaczego pole prostopadłościanu jest ważne w geometrii?

Pole powierzchni prostopadłościanu, będące sumą pól jego ścian, odgrywa istotną rolę w geometrii. Umożliwia nam precyzyjne oszacowanie całkowitej powierzchni bryły. Wiedza na temat obliczania pola powierzchni prostopadłościanu stanowi kluczowy element dla uczniów, studentów i wszystkich pasjonatów matematyki.

Obliczenia związane z polem powierzchni tego obiektu mają szerokie zastosowanie w różnych dziedzinach, takich jak:

• w budownictwie, gdzie dokładne wyliczenie powierzchni ścian pozwala na odpowiednie oszacowanie potrzebnych materiałów, takich jak farba czy płyty kartonowo-gipsowe,
• w pakowaniu, gdzie umiejętność obliczania tego pola ma duże znaczenie w optymalizacji wykorzystania przestrzeni w kartonach oraz pojemnikach,
• w naukach ścisłych, gdzie zrozumienie tej koncepcji wspiera rozwój umiejętności matematycznych.

Rozumienie, jak obliczać całkowite pole powierzchni prostopadłościanu, rozwija także umiejętności matematyczne. To z kolei prowadzi do lepszego przyswajania bardziej zaawansowanych tematów w matematyce. Nauka wyznaczania pola i objętości prostopadłościanu stanowi solidny fundament dla dalszego zgłębiania geometrii i innych dziedzin matematyki.

Jak wygląda wzór na pole prostopadłościanu?

Wzór na pole prostopadłościanu odgrywa kluczową rolę w geometrii. Pozwala na obliczenie całkowitej powierzchni tej bryły. W matematyce formuła ta przyjmuje postać P = 2(ab + ac + bc), gdzie a, b i c oznaczają długości krawędzi prostopadłościanu. Ta relacja uwzględnia wszystkie jego sześć ścian, tworząc trzy zestawy prostokątnych ścian o identycznych wymiarach.

Podstawowy wzór na powierzchnię prostopadłościanu znajduje zastosowanie w wielu dziedzinach, takich jak:

• architektura,
• budownictwo,
• inżynieria,
• projektowanie przestrzenne,
• analiza danych.

Dokładność obliczeń jest niezwykle istotna. Dzięki temu wzorowi można szybko i efektywnie obliczyć pole powierzchni, korzystając z dostępnych wymiarów, co znacznie ułatwia proces obliczeniowy.

Aby stosowanie wzoru było prawidłowe, kluczowe jest zapewnienie, że wszystkie wartości są wyrażone w tych samych jednostkach, na przykład w centymetrach lub metrach. Takie podejście nie tylko minimalizuje ryzyko pomyłek, ale także ułatwia analizę otrzymanych wyników.

Jak wyrazić wzór na pole powierzchni całkowitej prostopadłościanu?

Aby obliczyć całkowite pole powierzchni prostopadłościanu, wystarczy zastosować odpowiednią formułę. Używamy wzoru:

P_c = 2(ab + ah + bh)

W tym równaniu:

• a i b reprezentują długości krawędzi podstawy prostopadłościanu,
• h oznacza wysokość obiektu.

Możemy także posłużyć się innym zapisem wzoru:

P_c = 2ab + 2ah + 2bh

Czyli całkowita powierzchnia to suma powierzchni wszystkich sześciu prostokątnych ścianek. Dzięki temu wzorowi, realizacja obliczeń staje się łatwa i intuicyjna. Tego rodzaju obliczenia są szczególnie ważne w kontekście pakowania towarów czy też w branży budowlanej.

Co oznaczają symbole a, b, h w wzorze?

Symbole a, b i h w formule na pole powierzchni prostopadłościanu odpowiadają podstawowym wymiarom tego obiektu. a to długość, b to szerokość, a h oznacza wysokość. Te trzy parametry są niezwykle istotne, gdyż wpływają na kształt oraz rozmiar bryły.

Aby obliczyć pole powierzchni prostopadłościanu, niezbędne jest zrozumienie tych wymiarów. Kluczowe jest dokładne zmierzenie wszystkich krawędzi. Dopiero wtedy można otrzymać precyzyjne wyniki przy obliczaniu zarówno pola powierzchni, jak i objętości.

Na przykład, jeśli:

• długość wynosi 5 cm,
• szerokość wynosi 3 cm,
• a wysokość wynosi 4 cm,

można bez trudu wprowadzić te wartości do wzoru. Dzięki temu szybko uzyskamy całkowitą powierzchnię prostopadłościanu.

Jak oblicza się pole prostopadłościanu krok po kroku?

Obliczanie pola powierzchni prostopadłościanu to zadanie, które można zrealizować w kilku prostych krokach. Kluczowe jest, aby na początku znać wymiary tego obiektu, a więc zidentyfikować długości krawędzi, które oznaczymy jako a, b oraz c.

1. wysiłanie obliczenia pola podstawy przez pomnożenie długości dwóch sąsiadujących krawędzi: a oraz b,
2. obliczenie pól dwóch ścian bocznych: dla jednej zastosujemy wzór a × c, natomiast dla drugiej b × c,
3. suma trzech obliczonych pól,
4. wzór na pole powierzchni prostopadłościanu: P = 2(ab + ac + bc),
5. przedstawienie wyniku w odpowiednich jednostkach, takich jak cm² lub m².

Kiedy mamy do czynienia z dużymi wartościami, obliczenia mogą być znacznie ułatwione przez użycie kalkulatora.

Jak dobrać odpowiednie jednostki do obliczeń – cm, m?

Wybierając jednostki do obliczeń pola powierzchni prostopadłościanu, ważne jest, by zastosowane jednostki były spójne. Najczęściej posługujemy się centymetrami (cm) oraz metrami (m). Pole powierzchni wyrażamy w jednostkach kwadratowych, takich jak cm² lub m².

Aby uzyskać prawidłowy wynik, wszystkie wymiary prostopadłościanu powinny być w tych samych jednostkach. Na przykład, jeśli długości krawędzi podajemy w centymetrach, obliczenia należy przeprowadzić w cm². Spójność jednostek odgrywa kluczową rolę dla poprawności oraz czytelności wyników.

Dla przykładu, jeżeli wymiary krawędzi prostopadłościanu to:

• 2 cm,
• 3 cm,
• 4 cm,

zastosowanie odpowiedniego wzoru umożliwi nam obliczenie pola powierzchni, które wyniesie 24 cm². Z kolei, gdy wymiary wynoszą:

• 0,2 m,
• 0,3 m,
• 0,4 m,

otrzymany wynik będzie równy 0,24 m².

Wybór odpowiednich jednostek ma istotne znaczenie nie tylko dla samego obliczenia, ale także dla interpretacji wyników i ich praktycznego zastosowania w różnych dziedzinach, takich jak budownictwo czy projektowanie.

Czy można wykorzystać kalkulator do obliczeń pola?

Kalkulator to niezwykle przydatne narzędzie, które znacznie upraszcza obliczanie powierzchni prostopadłościanu. Wystarczy wprowadzić wymiary a, b oraz c, aby instantnie otrzymać wyniki dla każdego z parametrów. Dodatkowo, za pomocą prostego wzoru P = 2(ab + ac + bc), można szybko obliczyć całkowitą powierzchnię.

Korzystanie z kalkulatora znacząco obniża ryzyko wystąpienia błędów, które są częste w manualnych obliczeniach, szczególnie podczas:

• mnożenia,
• dodawania,
• liczenia wymiarów,
• obliczania powierzchni,
• rozwiązywania zadań geometrii.

Dzięki temu proces staje się nie tylko bardziej wydajny, ale przede wszystkim precyzyjny. Jest to kluczowe, zwłaszcza w zadaniach z geometrii oraz w realnych zastosowaniach związanych z prostopadłościanami.

Jak wyznaczyć pole podstawy i pole boczne prostopadłościanu?

Aby określić pole podstawy i pole boczne prostopadłościanu, najpierw musimy poznać jego wymiary.

Pole podstawy, które ma formę prostokąta, możemy obliczyć przy pomocy następującego wzoru:

P_podstawy = a × b

gdzie a i b to długości boków prostokąta.

Z kolei pole boczne, które obejmuje cztery krawędzie ścian, wyliczamy korzystając z formuły:

P_b = 2h(a + b)

W tym przypadku h oznacza wysokość prostopadłościanu.

Zrozumienie metod obliczania zarówno pola podstawy, jak i pola bocznego jest niezwykle istotne. To wiedza, która później umożliwia nam obliczenie całkowitej powierzchni prostopadłościanu. W praktyce ma to duże znaczenie w takich dziedzinach jak:

• geometria,
• projektowanie,
• budownictwo.

Jaki jest wzór na pole podstawy?

• pole podstawy prostopadłościanu obliczamy,
• wystarczy pomnożyć długości boków a i b,
• wzór to P_podstawy = a × b,
• a i b to długości krawędzi prostokątnej podstawy,
• uzyskaną wartość możemy wykorzystać w dalszych obliczeniach.

Proste mnożenie długości boków umożliwia szybkie uzyskanie tego istotnego parametru geometrycznego. Jest to niezwykle ważne w wielu dziedzinach, jak budownictwo czy pakowanie. Dzięki temu, nasze obliczenia stają się bardziej efektywne i praktyczne.

Jak obliczyć pole boczne?

Aby obliczyć pole boczne prostopadłościanu, mamy do dyspozycji dwa przydatne wzory:

1. P_b = 2h(a + b), gdzie h oznacza wysokość prostopadłościanu, a a oraz b to długości jego podstawy. Pole boczne zawiera w sobie powierzchnię dwóch par równoległych ścian, co uzyskujemy poprzez mnożenie wysokości przez sumę długości boków,
2. P_b = 2(ac + bc), gdzie a i b to długości boków podstawy, a c to wysokość ścian bocznych.

Te formuły znacznie ułatwiają obliczenia i są niezwykle przydatne w różnych dziedzinach związanych z geometrią oraz inżynierią.

Znajomość sposobów obliczania pola bocznego prostopadłościanu ma wiele praktycznych zastosowań, w tym:

• rozwiązywanie problemów w życiu codziennym,
• zastosowanie w pracy zawodowej,
• wsparcie w projektach inżynieryjnych.

Jak suma powierzchni ścian tworzy pole prostopadłościanu?

Pole powierzchni prostopadłościanu oblicza się jako sumę pól wszystkich jego ścianek. Taki bryła ma sześć ścian, podzielonych na trzy pary przeciwnych prostokątów. Każda z par ma identyczne wymiary, co sprawia, że obliczenia stają się znacznie prostsze.

Aby określić całkowite pole powierzchni, zaczynamy od obliczenia pola dla każdej z trzech par ścian:

1. Pierwsza para: Dla wymiarów a i b, pole jednej ściany wynosi ab, więc dla obu ścian otrzymujemy 2(ab).
2. Druga para: Rozpatrując wymiary a i h, pole wynosi 2(ah).
3. Trzecia para: W przypadku wymiarów b i h, obliczamy 2(bh).

Dodając te wartości, uzyskujemy całkowite pole powierzchni prostopadłościanu. Można to zapisać za pomocą wzoru:

P = 2(ab + ah + bh)

Ten wzór doskonale ilustruje, jak poszczególne pary ścian współdziałają w kształtowaniu całkowitej powierzchni bryły.

Zrozumienie sumy pól ścianek jest kluczowe w geometrii, ponieważ pozwala nam uchwycić przestrzeń zajmowaną przez obiekty. Oprócz tego, ma praktyczne zastosowanie, na przykład w obliczeniach materiałów potrzebnych do pokrycia konkretnej powierzchni.

Jak siatka prostopadłościanu pomaga w obliczaniu pola?

Siatka prostopadłościanu to niezwykle przydatne narzędzie, które pozwala obliczyć pole powierzchni tej bryły. Przedstawia wszystkie jego ściany w jednej płaszczyźnie, co znacznie ułatwia obliczenia dla każdej z prostokątnych powierzchni.

Zrozumienie struktury prostopadłościanu dzięki siatce wpływa pozytywnie na określenie jego wymiarów oraz przeprowadzenie niezbędnych kalkulacji. Ta wizualizacja ukazuje trzy pary prostokątnych ścian, co pozwala szybko dostrzec, które powierzchnie należy zsumować.

Aby obliczyć pole powierzchni prostopadłościanu, wystarczy dodać pola wszystkich sześciu prostokątów, mając na uwadze znane długości i szerokości. Dodatkowo, siatka znacznie ułatwia identyfikację pól podstawy oraz ścian bocznych. Taki sposób przedstawienia sprawia, że cały proces staje się bardziej przystępny, co jest szczególnie cenne dla uczniów i osób, które stawiają pierwsze kroki w geometrii.

Z pomocą siatki skomplikowane obliczenia stają się bardziej intuicyjne. To sprzyja efektywnemu uczeniu się matematyki oraz rozwiązywaniu zadań dotyczących prostopadłościanów.

Jak praktyczne zastosowania wykorzystują pole prostopadłościanu?

Zastosowania pola prostopadłościanu są naprawdę różnorodne i odgrywają istotną rolę w najrozmaitszych dziedzinach. Na przykład, w sektorze budowlanym, precyzyjne obliczenie powierzchni tego kształtu umożliwia dokładne oszacowanie ilości farby potrzebnej do pomalowania ścian. Tego typu wyliczenia są kluczowe, aby uniknąć marnotrawstwa materiałów i nieprzewidzianych wydatków.

W kontekście kafelka, umiejętność precyzyjnego obliczenia powierzchni podłóg oraz ścian jest bardzo przydatna, ponieważ pozwala właściwie zaplanować liczbę potrzebnych płytek. To z kolei wpływa na wydajność oraz jakość finalnych prac. W logistyce z kolei wiedza o powierzchni prostopadłościanu okazuje się być istotna przy pakowaniu. Dzięki temu można określić, ile produktów zmieści się w danej paczce, co jest kluczowe dla skutecznego zarządzania zapasami.

Należy również podkreślić, że precyzyjne obliczenia przyczyniają się do oszczędności oraz zwiększenia efektywności realizowanych projektów. Prawidłowe zastosowanie wzoru na pole prostopadłościanu, w połączeniu z dokładnym zrozumieniem jego właściwości, sprzyja lepszej organizacji działań w budownictwie, pakowaniu oraz wielu innych branżach.

Jak pole powierzchni pomaga w kafelkowaniu lub pakowaniu?

Pole powierzchni prostopadłościanu odgrywa istotną rolę w różnych codziennych sytuacjach, takich jak:

• kafelkowanie,
• pakowanie,
• optymalizacja wykorzystania przestrzeni.

Gdy obliczamy to pole, jesteśmy w stanie precyzyjnie oszacować ilość potrzebnego materiału, na przykład płytek ceramicznych, do pokrycia konkretnej powierzchni. Dzięki temu unikamy zakupu nadmiaru materiałów, co przekłada się na oszczędności finansowe.

W przypadku pakowania, znajomość pola powierzchni ułatwia optymalne wykorzystanie przestrzeni w opakowaniach. Mając świadomość wymiarów danego obiektu oraz jego powierzchni, możemy lepiej zaplanować rozmieszczenie produktów w pudełkach. To z kolei pozwala na maksymalne wykorzystanie dostępnej przestrzeni, a także na obniżenie kosztów transportu.

Z tych powodów, obliczanie pola powierzchni prostopadłościanu jest kluczowym elementem w wielu praktycznych zastosowaniach.

Jakie są zadania z obliczaniem pola prostopadłościanu?

Zadania związane z obliczaniem pola prostopadłościanu opierają się na następującym wzorze: P = 2(ab + ac + bc). Dzięki temu równaniu można określić całkowitą powierzchnię prostopadłościanu. Kluczowe jest zrozumienie różnych elementów tego kształtu, aby prawidłowo dobrać wymiary oraz jednostki.

W wielu standardowych problemach spotykamy się z obliczeniami:

• pola podstawy,
• bocznym,
• oraz całkowitym tego bryły.

Na przykład, aby obliczyć pole podstawy, wystarczy zastosować wzór: P_pod = a * b, gdzie a i b to długości boków prostokątnej podstawy. Z kolei do wyliczenia pola bocznego posłużymy się równaniem: P_bocz = 2h(a + b), w którym h oznacza wysokość prostopadłościanu.

Interaktywne zadania często umożliwiają praktyczne zastosowanie tych wzorów, znacznie ułatwiając proces nauki. Na przykład, dla prostopadłościanu o wymiarach 5 cm, 4 cm i 10 cm, możemy wyliczyć, że jego całkowita powierzchnia wynosi 220 cm².

Podczas rozwiązywania zadań uczniowie mogą napotykać typowe pułapki. Bardzo często mylą jednostki lub wpisują niewłaściwe wymiary do wzorów. Dlatego tak istotne jest, aby ćwiczyć oraz zrozumieć każdy krok obliczeniowy, co pozwoli na uzyskanie poprawnych wyników.

Jak rozwiązać przykładowe zadanie krok po kroku?

Aby obliczyć pole prostopadłościanu, warto podejść do tego zadania z systematycznym planem. Na początek zdefiniujmy wymiary: a to długość, b to szerokość, a h to wysokość.

Oto kroki do obliczenia:

1. Obliczenie pola podstawy za pomocą wzoru:
   \[ P_{podstawy} = a \times b \]
2. Obliczenie powierzchni ścian bocznych:
   • Dla dwóch ścian o wymiarach a i h:
     \[ P_{boczne1} = a \times h \]
   • Dla pozostałych dwóch ścian o wymiarach b i h:
     \[ P_{boczne2} = b \times h \]
3. Sumowanie powierzchni:
   \[ P_{boczne\_całkowite} = 2 \times (P_{boczne1} + P_{boczne2}) \]
4. Dodanie pola podstawy do łącznej powierzchni bocznej:
   \[ P_{całkowite} = 2 \times P_{podstawy} + P_{boczne\_całkowite} \]

Mnożymy pole podstawy przez dwa, aby uwzględnić obie podstawy prostopadłościanu. Na koniec, nie zapominajmy o podawaniu wymiarów w odpowiednich jednostkach, takich jak centymetry bądź metry.

Podejście to ułatwia zrozumienie całego procesu obliczeniowego, gwarantując jednocześnie precyzyjność wyników. Dzięki temu, krok po kroku, można z łatwością podjąć się zadań związanych z obliczaniem pola prostopadłościanu.

Jakie są typowe błędy w zadaniach z polem prostopadłościanu?

Typowe błędy przy obliczaniu pola prostopadłościanu najczęściej wynikają z niewłaściwego użycia wzorów i jednostek. Często spotykamy się z problemem mieszania centymetrów z metrami, co prowadzi do błędnych wyników. Dlatego kluczowe jest, aby zawsze trzymać się tych samych jednostek podczas obliczeń.

Innym częstym błędem jest pomijanie jednej z par ścian podczas sumowania pól. Pamiętajmy, że prostopadłościan składa się z 6 ścian, a ich pola musimy uwzględnić według wzoru P = 2(ab + ac + bc). Kiedy pomijamy jedno z wymiarów, tracimy istotną część obliczeń.

Zdarza się także, że źle podstawiamy wymiary do wzoru lub popełniamy błędy w mnożeniu, na przykład przez 2. Z tego powodu warto skrupulatnie sprawdzić wprowadzone dane oraz przeprowadzone działania matematyczne. Dzięki temu możemy uniknąć wielu powszechnych pułapek w obliczeniach.

Czy pole prostopadłościanu różni się od pola sześcianu?

Pola prostopadłościanu i sześcianu różnią się przede wszystkim wymiarami ich krawędzi. Sześcian to szczególny przypadek prostopadłościanu, w którym wszystkie krawędzie mają tę samą długość (a = b = c). W związku z tym, pole powierzchni sześcianu wyliczamy przy użyciu formuły P = 6a². Z kolei prostopadłościan posiada różnorodne wymiary i, co za tym idzie, różne pole powierzchni.

Aby obliczyć powierzchnię prostopadłościanu, stosujemy wzór P = 2(ab + ac + bc), gdzie a, b i c reprezentują długości krawędzi. Taki układ pozwala uwzględnić różnice w wymiarach, które są kluczowe dla uzyskania dokładnych wyników. To właśnie te odmienności w kształcie mają wpływ na wartości pól powierzchni.

Znaczenie tych różnic staje się oczywiste w praktyce, ponieważ obliczanie pola dla prostopadłościanu o różnych wymiarach bywa znacznie bardziej skomplikowane niż dla sześcianu. W dziedzinach takich jak inżynieria czy budownictwo, dokładne określenie pola powierzchni jest niezbędne do skutecznego projektowania i późniejszego wykorzystania bryły. Dlatego znajomość wzorów zarówno dla prostopadłościanu, jak i sześcianu jest niezwykle istotna.

Jakie wzory związane z prostopadłościanem warto znać?

Wzory związane z prostopadłościanami mają ogromne znaczenie zarówno w matematyce, jak i w praktycznych zastosowaniach. Kluczowym z nich jest formuła na całkowite pole powierzchni, która przyjmuje postać P = 2(ab + ac + bc). Dzięki temu równaniu można łatwo obliczyć całkowity obszar prostopadłościanu, gdzie a, b oraz c oznaczają długości jego krawędzi.

Inny znaczący wzór dotyczy pola bocznego prostopadłościanu, które wyraża się jako P_b = 2h(a + b). Jest on szczególnie przydatny w kontekście obliczania powierzchni ścian bocznych, co ma istotne znaczenie na przykład w:

• budownictwie,
• projektowaniu wnętrz,
• obliczaniu powierzchni mebli.

Aby ustalić pole jednej z podstaw prostopadłościanu, stosujemy prostą formułę P_podstawy = a × b.

Ważnym aspektem jest również wzór na objętość prostopadłościanu, wyrażony jako V = a × b × c. Ma on kluczowe znaczenie w sytuacjach, w których istotne jest określenie, ile przestrzeni zajmuje dany obiekt. Również długość przekątnej prostopadłościanu jest istotna w analizach geometrycznych i architektonicznych, wyrażana wzorem d = √(a² + b² + c²).

Dzięki zrozumieniu tych wzorów, możliwe staje się sprawne rozwiązanie zadań z geometrii oraz inżynierii. Co więcej, wiele z tych formuł ma praktyczne zastosowanie w codziennym życiu, takich jak:

• obliczenia potrzebne przy pakowaniu,
• kafelkowaniu,
• budowie różnych konstrukcji.

Jak obliczyć objętość prostopadłościanu?

Aby określić objętość prostopadłościanu, stosujemy formułę V = a × b × c. W niej a, b oraz c to długości krawędzi tej bryły. Objętość (V) informuje nas, jaką przestrzeń zajmuje prostopadłościan. Ważne jest, aby wymiary krawędzi były wyrażone w tych samych jednostkach – na przykład centymetrach lub metrach.

Przykładowo, jeśli długości krawędzi wynoszą 3 cm, 4 cm i 5 cm, możemy łatwo obliczyć objętość:

• V = 3 cm × 4 cm × 5 cm,
• co wynosi 60 cm³.

Objętość ma ogromne znaczenie nie tylko w matematyce, ale także w codziennych zastosowaniach. W takich obszarach jak:

• pakowanie towarów,
• budownictwo,
• ustalanie potrzebnej przestrzeni do przechowywania różnych materiałów.

Jak wyznaczyć długości krawędzi prostopadłościanu?

Aby określić długości krawędzi prostopadłościanu, wymagane są trzy kluczowe wymiary: długość (a), szerokość (b) oraz wysokość (c). Można je uzyskać z różnych źródeł, takich jak:

• rysunki techniczne,
• pomiary ręczne,
• specyfikacje.

W sytuacji braku bezpośrednich pomiarów, długość przekątnej można obliczyć przy użyciu wzoru: d = √(a² + b² + c²).

Zrozumienie długości krawędzi jest niezwykle ważne dla dalszych obliczeń, takich jak:

• pole powierzchni,
• objętość prostopadłościanu.

Co więcej, zewnętrzne wymiary wpływają na fizyczne właściwości bryły, które mogą mieć kluczowe znaczenie w kontekście pakowania oraz zastosowań w różnych dziedzinach inżynierii i architektury.