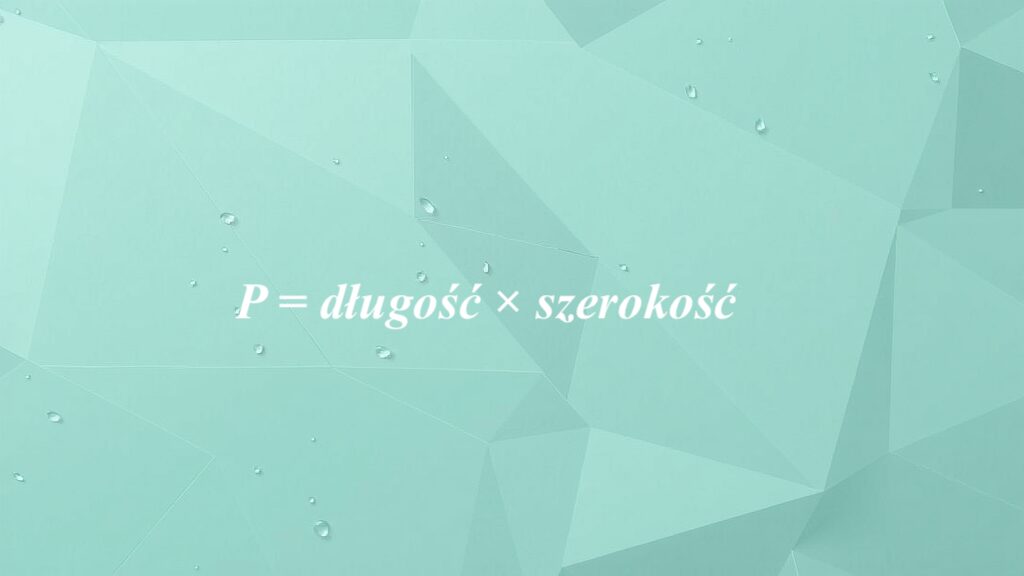Wzór na pole prostokąta

Czym jest prostokąt i jakie ma właściwości?

Prostokąt to wyjątkowy rodzaj czworokąta, który charakteryzuje się czterema bokami, z których przeciwległe mają tę samą długość. Dodatkowo, każdy z kątów prostokąta wynosi dokładnie 90 stopni. Do jego kluczowych cech można zaliczyć równoległość boków oraz ich równość, co sprawia, że jest on szczególnym przypadkiem równoległoboku, który także dysponuje parami równoległych boków.

Obliczanie długości przekątnych prostokąta jest proste dzięki twierdzeniu Pitagorasa. W skrócie, długość przekątnej (oznaczanej jako d) można znaleźć przy pomocy wzoru: d = √(a² + b²), gdzie a to długość, a b to szerokość prostokąta. Co ciekawe, obie przekątne mają tę samą długość, a ich punkt przecięcia dzieli je na dwie równe części.

Prostokąt posiada również szereg innych istotnych właściwości:

• Pole można obliczyć jako iloczyn długości i szerokości,
• Obwód to suma długości wszystkich boków, co jest również istotnym parametrem,
• Symetria: Prostokąt wykazuje symetrię względem obu osi, co ma zastosowanie w różnych dziedzinach, od architektury po grafikę.

Te geometrie znajdują zastosowanie w licznych dziedzinach, w tym w budownictwie oraz planowaniu przestrzeni. Doskonale sprawdzają się także w codziennych projektach dotyczących aranżacji pomieszczeń i mebli. Z tego powodu prostokąt jest jednym z fundamentalnych kształtów zarówno w teorii geometrii, jak i w praktycznych aspektach życia codziennego.

Jakie są zastosowania pola prostokąta w codziennym życiu?

Pole prostokąta znajduje wiele praktycznych zastosowań, które na co dzień wpływają na nasze życie. W dziedzinach takich jak architektura i budownictwo, stanowi ono kluczowy element przy obliczaniu powierzchni różnych pomieszczeń. To z kolei pozwala na lepsze zaplanowanie ilości materiałów, na przykład paneli podłogowych czy farb, dzięki czemu można efektywniej aranżować meble oraz dobierać wyposażenie wnętrz, co jest niezwykle istotne w procesie projektowania mieszkań oraz biur.

W ogrodnictwie pole prostokąta odgrywa ważną rolę w organizacji przestrzeni. Ułatwia ono odpowiednie rozmieszczanie roślin oraz dekoracji, co sprawia, że łatwiej jest kontrolować, ile miejsca zajmują rabaty, ścieżki i inne elementy. Taka znajomość powierzchni przyczynia się do stworzenia harmonijnej kompozycji w ogrodzie.

Również dekoratorzy wnętrz chętnie korzystają z tego wzoru. Kiedy wybierają dywany, płytki czy inne dodatki, obliczenia oparte na polu prostokąta pomagają im zadbać o odpowiednie proporcje oraz rozmiary wszystkich elementów. W stolarstwie natomiast, obliczanie powierzchni drewna niezbędnego do produkcji mebli i konstrukcji opiera się na tych samych zasadach.

Geodezja również stosuje pole prostokąta w swoich pomiarach oraz wyznaczaniu terenów. Ten aspekt jest kluczowy przy planowaniu przestrzennym oraz podejmowaniu lokalnych inwestycji gruntowych. W kontekście edukacji, zwłaszcza przygotowując uczniów do matury, różnorodność zastosowań pola prostokąta ma istotne znaczenie. Umożliwia to studentom rozwijanie analitycznego myślenia oraz umiejętności matematycznych.

Warto znać te wszystkie zastosowania, aby skutecznie wykorzystywać wzór na pole prostokąta w praktycznych sytuacjach. Dzięki temu można podejmować mądre decyzje w różnych aspektach życia.

Jak obliczyć pole prostokąta?

Aby ustalić pole prostokąta, można z powodzeniem zastosować prosty wzór: P = a · b. W tej formule P reprezentuje pole, natomiast a i b to długość i szerokość prostokąta. Kluczowe jest, aby zarówno długość, jak i szerokość były wyrażone w tych samych jednostkach. Dzięki temu uzyskany wynik będzie w jednostkach kwadratowych, na przykład w metrach kwadratowych (m²) lub centymetrach kwadratowych (cm²).

Dla ilustracji, przyjmijmy, że długość prostokąta wynosi 5 metrów, a szerokość 3 metry. Wówczas obliczenie wygląda następująco: 5 m · 3 m równa się 15 m². Tego typu wzór ma szerokie zastosowanie w geometrii, ale także odnajduje swoje praktyczne znaczenie w życiu codziennym. Może być przydatny przy:

• planowaniu przestrzeni w pomieszczeniach,
• szacowaniu potrzebnych materiałów budowlanych.

Wzór na pole prostokąta: iloczyn długości i szerokości

Wzór na obliczenie pola prostokąta jest bardzo prosty: P = a × b. W tym równaniu P odnosi się do powierzchni prostokąta, podczas gdy a i b reprezentują długości jego boków. Aby uzyskać pole, wystarczy pomnożyć długość przez szerokość. Przykładowo, jeśli długość prostokąta to 5 metrów, a jego szerokość wynosi 3 metry, to obliczone pole będzie równe 15 metrom kwadratowym.

Ten prosty wzór odgrywa ważną rolę nie tylko w matematyce, ale także w takich dziedzinach jak:

• architektura,
• budownictwo,
• projektowanie.
• znalezienie powierzchni do pokrycia,
• oszacowanie kosztów materiałów.

Zrozumienie, jak obliczyć pole prostokąta, umożliwia skuteczne planowanie oraz precyzyjne pomiary przestrzeni. Co więcej, ten wzór znajduje zastosowanie w wielu codziennych sytuacjach. Na przykład, dokonując zakupu materiałów budowlanych, znajomość powierzchni pozwala określić, ile farby czy tapety będzie potrzebnych do pokrycia danego obszaru.

Co oznaczają długość i szerokość prostokąta?

Długość i szerokość prostokąta to podstawowe parametry, które definiują jego rozmiar oraz kształt. Długość, zazwyczaj oznaczana literą „a”, to jeden z boków prostokąta, który zazwyczaj jest dłuższy od pozostałych. Natomiast szerokość, symbolizowana jako „b”, to bok przylegający do długości, zwykle krótszy.

Te wymiary odgrywają istotną rolę w obliczeniach podstawowych właściwości prostokąta, takich jak:

• pole, które obliczamy, mnożąc długość przez szerokość (a × b), co pozwala uzyskać powierzchnię figury,
• obwód, który obliczamy, sumując długości wszystkich boków, stosując wzór: 2a + 2b.

Długość i szerokość prostokąta wyrażane są w różnych jednostkach, takich jak centymetry, metry czy cale. Dzięki temu prostokąty znajdują zastosowanie w wielu dziedzinach, od matematyki po architekturę, a nawet w codziennym życiu. Zrozumienie tych wymiarów jest kluczowe dla prowadzenia licznych obliczeń geometrycznych oraz przy projektowaniu.

Jakie jednostki stosuje się do pola prostokąta?

Jednostki służące do mierzenia pola prostokąta są jednostkami kwadratowymi, które odzwierciedlają powierzchnię. Najczęściej spotykamy:

• centymetr kwadratowy (cm²),
• metr kwadratowy (m²),
• ar (100 m²),
• hektar (10 000 m²).

Te miary znajdują zastosowanie w różnych kontekstach – od niewielkich pomieszczeń, takich jak pokoje, po znacznie większe obszary, na przykład działki budowlane czy boiska sportowe.

Centymetr kwadratowy cieszy się popularnością w edukacji i prostych projektach, natomiast metr kwadratowy jest powszechnie wykorzystywany w architekturze oraz budownictwie. Zrozumienie tych jednostek jest kluczowe, gdyż umożliwia precyzyjne obliczenia i efektywne wykorzystanie dostępnej przestrzeni. Właściwe podejście do pomiarów ma ogromne znaczenie zarówno w projektowaniu, jak i w rolnictwie.

Jak obliczyć pole prostokąta mając przekątną?

Istnieje interesujący sposób na obliczenie pola prostokąta, posługując się jedynie długością jego przekątnej oraz kątem, jaki tworzą przekątne. Przekątna, oznaczana literą „d”, łączy przeciwległe wierzchołki i jej długość można wyznaczyć przy pomocy twierdzenia Pitagorasa: d = √(a² + b²), gdzie „a” oraz „b” to długości boków prostokąta.

Aby uzyskać pole prostokąta, należy zastosować formułę: P = 1/2 d² sin(α), gdzie „α” to kąt między przekątnymi. Ta metoda jest szczególnie użyteczna w sytuacjach, gdy nie dysponujemy długościami boków, a jedynie przekątną i odpowiednim kątem. Dzięki temu rozwiązaniu możemy łatwo obliczyć pole, znając inne parametry prostokąta. To stanowi ciekawą alternatywę dla tradycyjnych metod.

Metody te umożliwiają obliczanie pola prostokąta z zastosowaniem przekątnej, co sprawia, że można uzyskiwać wyniki w bardziej złożonych przypadkach. Takie podejście zwiększa elastyczność w rozwiązywaniu różnorodnych problemów geometrycznych.

Wzór na pole prostokąta z wykorzystaniem twierdzenia Pitagorasa

Wzór na pole prostokąta można skonstruować, bazując na twierdzeniu Pitagorasa. Najważniejszymi elementami są:

• długość przekątnej,
• kąt, który ona tworzy.

Aby obliczyć długość przekątnej, posługujemy się równaniem: d = √(a² + b²), gdzie a i b oznaczają długości boków prostokąta.

Z pomocą twierdzenia Pitagorasa, mając długość przekątnej oraz kąt α między przekątnymi, możemy obliczyć pole prostokąta według równania: P = 1/2 d² sin(α). Ta technika łączy w sobie aspekty geometrii i trygonometrii, oferując alternatywne podejście do obliczeń. Jest to szczególnie pomocne w bardziej skomplikowanych problemach geometrycznych.

W praktycznych zastosowaniach istotne jest, aby znać relacje między bokami a przekątną, co znacznie ułatwia wszelkie obliczenia. Wiedza ta jest również nieoceniona przy rozwiązywaniu zagadnień związanych z polem prostokąta.

Jak odróżnić pole prostokąta od obwodu prostokąta?

Rozróżnienie między polem a obwodem prostokąta jest kluczowe w geometrii. Pole prostokąta, będące miarą jego powierzchni, oblicza się poprzez pomnożenie długości (a) przez szerokość (b). Używając wzoru P = a · b, wynik podawany jest w jednostkach kwadratowych, co odzwierciedla zajmowaną przez figurę powierzchnię.

Obwód prostokąta to całkowita długość jego granicy. Można go obliczyć, sumując długości wszystkich boków, wykorzystując wzór: Obwód = 2 × (a + b). Wynik tego obliczenia wyrażany jest w jednostkach liniowych, ponieważ odnosi się do długości, a nie do powierzchni.

Główna różnica między tymi dwoma pojęciami polega na tym, że:

• pole odnosi się do przestrzeni wewnętrznej figury,
• obwód dotyczy wirtualnej linii, która otacza ten kształt.

W praktyce, zwłaszcza w dziedzinach takich jak budownictwo czy architektura, znajomość obu tych pojęć jest kluczowa dla precyzyjnych obliczeń, które są niezbędne do efektywnego planowania przestrzeni oraz materiałów.

Jakie błędy popełniają uczniowie podczas obliczania pola prostokąta?

Uczniowie często wpadają w różnorodne pułapki, gdy próbują obliczyć pole prostokąta, co może prowadzić do błędnych rezultatów. Najczęstszym błędem jest mylenie obwodu z polem. Ważne jest, aby zrozumieć, że pole prostokąta to przestrzeń, jaką figura zajmuje, natomiast obwód odnosi się do sumy długości wszystkich krawędzi.

Innym problematycznym zagadnieniem jest nieprawidłowe stosowanie jednostek miary. Niezbyt doświadczeni uczniowie mogą nie zdawać sobie sprawy, że przy obliczaniu pola należy wykorzystywać jednostki kwadratowe, jak m² czy cm², a nie jedynie same metry lub centymetry.

Ponadto, wiele osób popełnia błędy przy mnożeniu długości i szerokości prostokątów. Często zdarza się, że zapominają o konieczności pomnożenia obu tych wymiarów, co prowadzi do niedoszacowania wyniku. Problemy mogą też wystąpić, gdy próbują obliczyć pole prostokątów na podstawie długości przekątnych, zwłaszcza przy zastosowaniu twierdzenia Pitagorasa.

Aby zredukować te nieprawidłowości, warto regularnie ćwiczyć konkretne zadania, korzystając z rozwiązań. Tego rodzaju praktyka nie tylko pomaga utrwalić wiedzę z zakresu matematyki, ale także rozwija umiejętności związane z obliczeniami.

Jak wykorzystać pole prostokąta w zadaniach matematycznych?

Pole prostokąta odgrywa istotną rolę w matematyce, szczególnie w kontekście rozwijania umiejętności analitycznych. Można je zastosować w różnych dziedzinach, takich jak:

• obliczanie powierzchni w projektach budowlanych,
• rozwiązywanie problemów geometrii w szkole,
• planowanie przestrzeni w pomieszczeniach.

Uczniowie powinni umieć wyznaczać brakujące wymiary, co czasami wymaga:

• rozwiązywania równań,
• stosowania właściwych wzorów.

W kontekście egzaminu maturalnego umiejętność obliczania pola prostokąta na podstawie różnych danych jest niezwykle ważna. Przykłady zadań matematycznych oraz zalecane ćwiczenia odgrywają kluczową rolę w utrwalaniu wiedzy uczniów. Zazwyczaj dotyczą praktycznych sytuacji, gdzie pole prostokąta znajduje zastosowanie.

Dzięki systematycznym ćwiczeniom uczniowie rozwijają swoje zdolności obliczeniowe oraz lepiej rozumieją zagadnienia geometryczne. Takie podejście sprzyja ich akademickiemu rozwojowi i ułatwia praktyczne zastosowanie matematyki w życiu.

Przykłady praktycznych zadań z rozwiązaniami

Przykłady praktycznych zadań z rozwiązaniami dotyczą obliczania pola prostokąta, a także pokazują, jak te obliczenia sprawdzają się w życiu codziennym. Oto kilka interesujących zadań:

1. Zadanie 1: Pola prostokąta o długości 8 cm i szerokości 5 cm.
   Rozwiązanie: Aby obliczyć pole prostokąta, posługujemy się wzorem: Pole = długość × szerokość. W tym przypadku więc: Pole = 8 cm × 5 cm, co daje nam 40 cm².
2. Zadanie 2: Znajdź obwód prostokąta o polu 50 cm² i szerokości 5 cm.
   Rozwiązanie: Najpierw musimy obliczyć długość. Znamy wzór: Pole = długość × szerokość. Przystępując do obliczeń, otrzymujemy: długość = Pole / szerokość = 50 cm² / 5 cm = 10 cm. Gdy mamy długość, możemy obliczyć obwód, korzystając ze wzoru: Obwód = 2 × (długość + szerokość) = 2 × (10 cm + 5 cm) = 30 cm.
3. Zadanie 3: Dany jest prostokąt z przekątną długości 13 cm oraz szerokością 5 cm. Jak znaleźć długość?
   Rozwiązanie: Wykorzystujemy twierdzenie Pitagorasa, według którego: Przekątna² = długość² + szerokość². Mamy zatem równanie: 13² = długość² + 5². Po przeprowadzeniu obliczeń dostajemy: 169 = długość² + 25, co upraszcza się do długość² = 144. Z tego wynika, że długość wynosi 12 cm.
4. Zadanie 4: Ile materiału potrzeba do pokrycia podłogi o wymiarach 4 m na 3 m?
   Rozwiązanie: Liczymy pole: Pole = 4 m × 3 m = 12 m².
5. Zadanie 5: W prostokącie, którego pole wynosi 36 m², długość jest dwa razy większa niż szerokość. Jakie są wymiary tego prostokąta?
   Rozwiązanie: Oznaczmy szerokość jako x, co sprawia, że długość to 2x. Można zatem zapisać równanie: 2x × x = 36, co upraszcza się do 2x² = 36. Z tego wyrażenia otrzymujemy x² = 18, a więc x = √18, co daje około 4.24 m. Długość prostokąta wyniesie 2√18, czyli około 8.49 m.

Zadania te doskonale ilustrują, jak praktycznie wykorzystać wzór na pole prostokąta w różnych okolicznościach, a każde rozwiązanie prowadzi nas przez kolejne kroki, rozwijając nasze umiejętności matematyczne.

Jakie są podobieństwa i różnice między prostokątem, kwadratem, rombem i równoległobokiem?

Prostokąt, kwadrat, romb oraz równoległobok to różne rodzaje czworokątów, które łączą pewne cechy, ale także mają wyraźne różnice. Wszystkie te figury mają cztery boki i zaliczają się do grupy figur płaskich.

• Prostokąt charakteryzuje się czterema kątami prostymi oraz dwiema parami równoległych boków,
• jego przeciwległe boki są równe, co sprawia, że łatwo można go zdefiniować,
• powierzchnię prostokąta oblicza się, mnożąc długość przez szerokość, co czyni go prostym w analizie.

Kwadrat to szczególny przypadek prostokąta, gdzie wszystkie boki mają tę samą długość, co wiąże się także z posiadaniem kątów prostych. Dzięki tej regularności kwadrat zyskuje na symetrii i estetyce.

Romb natomiast ma wszystkie boki równe, ale jego kąty niekoniecznie muszą być proste. Staje się kwadratem dopiero w momencie, gdy wszystkie kąty przyjmują wartość prostą, co tym samym zmienia jego charakter.

Równoległobok różni się od pozostałych wymienionych figur, ponieważ ma dwie pary równoległych boków, a jego kąty mogą być różnej wielkości. Powierzchnię równoległoboku oblicza się na podstawie jego wysokości i długości podstawy.

W skrócie, prostokąt i kwadrat wyróżniają się kątami prostymi, podczas gdy romb i równoległobok mogą mieć różne kąty. Te różnice wpływają na zastosowania oraz właściwości tych figur geometrycznych, które są niezwykle istotne w matematyce i codziennym życiu.

Jak pole prostokąta wykorzystywane jest w architekturze i budownictwie?

Pole prostokąta zajmuje kluczowe miejsce w architekturze i budownictwie, odgrywając nieodzowną rolę w planowaniu przestrzeni. Wiedza na temat jego powierzchni umożliwia architektom i inżynierom precyzyjne wytyczanie wymiarów pomieszczeń, co jest istotne dla skutecznego projektowania oraz weryfikacji rozmiarów konstrukcji.

Zastosowania obliczeń związanych z polem prostokąta są niezwykle różnorodne. Dzięki nim można:

• dokładnie oszacować ilość materiałów budowlanych,
• obliczyć powierzchnię płytek,
• określić ilość farby potrzebnej do malowania,
• oszacować powierzchnię podłóg,
• wspierać planowanie układów ścian.

Umiejętność szybkiego obliczania pola prostokąta znacząco ułatwia realizację projektów w branży budowlanej. Takie podejście pozwala zredukować ryzyko błędów, co wpływa na zwiększenie efektywności pracy. Dlatego też pole prostokąta stanowi fundament wszelkich działań projektowych w obszarze architektury i budownictwa.

Jak obliczyć proporcje i złoty prostokąt?

Aby obliczyć proporcje w złotym prostokącie, warto najpierw zrozumieć jego charakterystyczny kształt, który ma stosunek długości do szerokości równy około 1,618 – to tzw. złota proporcja (φ). Można to przedstawić w formie matematycznej. Zakładając, że długość prostokąta to „a”, a szerokość to „b”, postępuj według następujących kroków:

1. Oblicz stosunek: Podziel dłuższy bok (a) przez krótszy bok (b):

proporcja = a / b

2. Sprawdź zbliżenie do złotej proporcji: Zobacz, czy wynik jest bliski 1,618.

Jeśli się zgadza, oznacza to, że twój prostokąt ma cechy złotego prostokąta. Taki kształt jest bardzo ceniony w architekturze i sztuce ze względu na swoje harmonijne i estetyczne właściwości. Uwzględniając tę proporcję w projektach, można uzyskać zrównoważony i przyjemny dla oka efekt.

Możesz również stworzyć złoty prostokąt, zaczynając od jednego z wymiarów, a następnie obliczając drugi. Pamiętaj, że można to zapisać jako:

b = a / φ

gdzie „a” to długość, a „b” to szerokość. W rzeczywistości, zastosowanie wzorów i cech złotego prostokąta znajduje swoje miejsce w dekoracji, architekturze oraz w wielu innych dziedzinach designu.

W jaki sposób pole prostokąta pomaga w ogrodnictwie, dekoratorstwie i stolarstwie?

Pole prostokąta jest niezwykle ważne w ogrodnictwie, dekoratorstwie i stolarstwie. Ta wiedza pozwala na efektywne planowanie oraz realizację różnorodnych projektów.

W ogrodnictwie znajomość powierzchni pomaga ustalić, ile roślin można umieścić na określonym terenie. Na przykład, przy projektowaniu ogrodu czy trawnika, obliczenie pola prostokąta ułatwia optymalne rozmieszczenie roślin, co z kolei wpływa na ich zdrowie i estetykę przestrzeni.

W dekoratorstwie ta sama umiejętność odgrywa kluczową rolę przy doborze materiałów i ustawieniu dekoracji. Gdy właściciele urządzają swoje mieszkania, mogą ocenić wymiary mebli oraz liczbę niezbędnych dodatków. To podejście pozwala na stworzenie harmonijnej i przemyślanej kompozycji przestrzeni.

Z kolei w stolarstwie znajomość pola prostokąta jest niezbędna do precyzyjnego cięcia drewna. Podczas produkcji mebli bądź innych konstrukcji, rzemieślnicy obliczają powierzchnię, co sprzyja efektywnemu wykorzystaniu materiałów oraz minimalizacji odpadów. Przykłady to między innymi wytwarzanie:

• półek,
• stołów,
• szafek.

Te różnorodne zastosowania sprawiają, że pole prostokąta staje się nie tylko teoretycznym pojęciem matematycznym, ale także praktycznym narzędziem wykorzystywanym na co dzień w ogrodnictwie, dekoratorstwie i stolarstwie, wspierając realizację kreatywnych projektów.