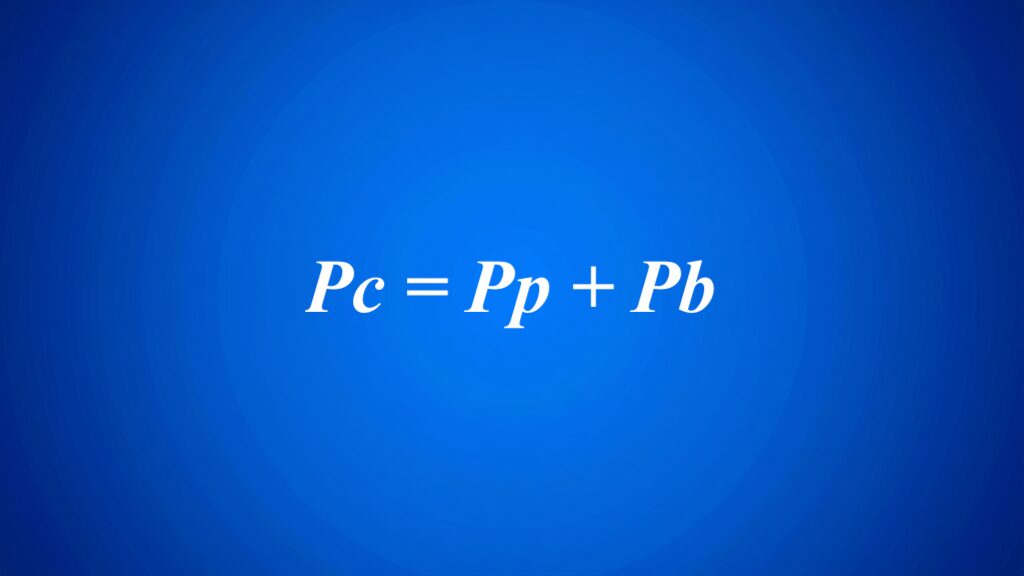Wzór na pole ostrosłupa

Ostrosłup to geometryczna figura, która składa się z jednej podstawy w postaci wielokąta oraz bocznych ścian, które mają formę trójkątów. W jego górnej części znajduje się wierzchołek, punkt, w którym zbiegają się wszystkie krawędzie boczne. Warto zaznaczyć, że podstawy ostrosłupów mogą mieć różnorodne kształty, takie jak:

kwadratowe,
prostokątne,
foremne.

A to z kolei wpływa na ich właściwości oraz sposób obliczania pól powierzchni.

Jedną z kluczowych cech ostrosłupów jest:

liczba krawędzi,
długości boków,
wysokość.

Liczba krawędzi ostrosłupa zawsze przewyższa o jeden liczbę krawędzi w podstawie. To zależność, która wynika z liczby boków tej podstawy. Na przykład, ostrosłup o kwadratowej podstawie ma osiem krawędzi, natomiast pięciokątny dysponuje dziesięcioma.

Wysokość ostrosłupa to odległość od wierzchołka do płaszczyzny jego podstawy. Ten wymiar jest niezwykle istotny, gdy chodzi o obliczanie powierzchni i objętości figury. Zrozumienie tych kształtów jest kluczowe w geometrii przestrzennej oraz w praktycznych zastosowaniach, takich jak architektura czy inżynieria budowlana. Ostrosłupy mają zatem znaczące znaczenie nie tylko w matematyce, ale również w różnych dziedzinach nauki i technologii.

Jakie są rodzaje ostrosłupów w geometrii przestrzennej?

Ostrosłupy w geometrii przestrzennej wyróżniają się różnorodnością, którą można określić na podstawie kształtu ich podstawy oraz liczby ścian bocznych. Poznajmy najważniejsze ich typy:

Ostrosłup prawidłowy – jego podstawą jest wielokąt foremny, a ściany boczne stanowią równoramienne trójkąty,
Ostrosłup prawidłowy czworokątny – wyróżnia się kwadratową podstawą oraz czterema identycznymi ścianami bocznymi, co zapewnia harmonijną konstrukcję,
Ostrosłup trójkątny – w tym przypadku podstawą jest trójkąt, a ściany boczne również przyjmują formę trójkątów, które mogą mieć równe boki,
Ostrosłup pięciokątny – jego pięciokątna podstawa prowadzi do pięciu ścian bocznych, co czyni jego strukturę bardziej złożoną,

Dzięki znajomości tych różnych rodzajów ostrosłupów możesz właściwie dobierać wzory do obliczeń pól i objętości tych brył, co jest niezwykle istotne w geometrii.

Jak wygląda siatka ostrosłupa?

Siatka ostrosłupa to niesamowicie pomocny dwuwymiarowy schemat przedstawiający jego budowę. Składa się ona z podstawy oraz trójkątnych ścian bocznych. W przypadku ostrosłupa prawidłowego czworokątnego, widnieje tam kwadrat jako podstawa, otoczony przez cztery identyczne trójkąty równoramienne, które pełnią rolę ścian bocznych. Taki układ pozwala lepiej zrozumieć kształt ostrosłupa i z znaczną łatwością wspiera obliczanie całkowitego pola powierzchni, co można osiągnąć przez sumowanie pól poszczególnych figur geometrycznych.

Korzystanie z siatki pozwala na szybką identyfikację wszystkich elementów ostrosłupa, co jest niezwykle ważne w zadaniach geometrycznych. Zrozumienie układu siatki ułatwia także wprowadzenie pojęć związanych z polem podstawy oraz całkowitą powierzchnią ostrosłupa, co sprawia, że staje się to kluczowym elementem edukacji w zakresie geometrii. Co więcej, umiejętność rysowania siatki ma zastosowanie nie tylko w nauce, ale również w szerokich obszarach, takich jak:

architektura,
projektowanie,
zrozumienie kształtów,
struktury,
fundamenty geometrii.

Jak działa wzór na pole ostrosłupa?

Wzór na pole ostrosłupa to kluczowy element w geometrii, który pozwala na obliczenie całkowitej powierzchni tego kształtu przestrzennego. Całkowite pole powierzchni ostrosłupa (Pc) stanowi sumę pola jego podstawy (Pp) oraz pola powierzchni bocznej (Pb), co można zapisać w prostej formie: Pc = Pp + Pb.

Dla ostrosłupa prawidłowego czworokątnego, którego krawędzie podstawy są równe, pole powierzchni wyliczamy przy użyciu wzoru: Pc = a² + 2ah. W tym równaniu „a” to długość krawędzi podstawy, a „h” to wysokość bocznych ścian. Te obliczenia okazują się niezwykle przydatne nie tylko w szkole, ale również w takich dziedzinach jak:

architektura,
inżynieria,
planowanie budynków,
ustalanie zapotrzebowania na materiały,
analiza objętości.

Co więcej, wzór na pole ostrosłupa często pojawia się w kontekście zadań związanych z analizą objętości oraz powierzchni różnorodnych obiektów. To czyni go niezbędnym narzędziem w wielu dziedzinach science i technologii.

Czym jest pole powierzchni całkowitej ostrosłupa?

Pole powierzchni całkowitej ostrosłupa, oznaczane jako Pc, to istotne pojęcie w geometrii. Obejmuje ono całkowitą powierzchnię, jaką dany ostrosłup zajmuje w przestrzeni. Możemy je obliczyć, korzystając z prostego wzoru:

Pc = Pp + Pb,

gdzie Pp odnosi się do pola podstawy, a Pb definiuje pole powierzchni bocznej ostrosłupa. Kluczowe jest, aby zsumować pola wszystkich ścian, ponieważ tylko w ten sposób można dokładnie określić, jaką przestrzeń zajmuje dany ostrosłup.

Zrozumienie tego zagadnienia ma znaczenie praktyczne. Na przykład w budownictwie projektowanie dachów czy konstrukcji oparte na formach ostrosłupa wymagają:

znajomości pole powierzchni całkowitej,
właściwego planowania materiałów budowlanych,
precyzyjnego obliczenia wymagań konstrukcyjnych,
uwzględnienia warunków atmosferycznych,
efektywności kosztowej projektów.

Ponadto, wiedza na temat wartości Pc jest przydatna w precyzyjnym planowaniu oraz realizacji różnorodnych projektów.

Czym jest pole powierzchni bocznej ostrosłupa?

Pole powierzchni bocznej ostrosłupa, znane jako Pb, odgrywa kluczową rolę w obliczeniach związanych z tą formą geometryczną. Jest to suma pól wszystkich trójkątnych ścian bocznych, co czyni dwa podstawowe wzory istotnymi. W przypadku ostrosłupa prawidłowego czworokątnego, w którym ściany boczne mają kształt trójkątów równoramiennych, pole to można obliczyć za pomocą wzoru: Pb = 2ah. W tej formule „a” oznacza długość krawędzi podstawy, natomiast „h” odnosi się do wysokości jednej ze ścian bocznych.

W praktyce wykorzystanie pola powierzchni bocznej ma ogromne znaczenie, szczególnie w branży budowlanej. Zastosowanie to wpływa na różne aspekty, takie jak:

dobór odpowiednich materiałów do pokrycia ścian bryły,
efektywne wykorzystanie przestrzeni,
właściwe planowanie materiałów budowlanych,
projektowanie architektoniczne,
efektywność działań inżynieryjnych.

Umiejętność obliczania Pb oraz zrozumienie tej koncepcji są nieocenione w takich dziedzinach jak matematyka czy inżynieria. Co więcej, zastosowania pola bocznego wykraczają poza teoretyczne obliczenia, znajdując zastosowanie również w praktyce budowlanej.

Czym jest pole podstawy ostrosłupa?

Pole podstawy ostrosłupa, znane jako Pp, odnosi się do powierzchni, która stanowi jego fundament. Może ono przybierać różnorodne kształty, ale najczęściej występują:

kwadraty,
prostokąty,
inne wielokąty foremne.

Aby obliczyć pole dla kwadratu, wykorzystuje się wzór a², gdzie a oznacza długość boku. Dla prostokąta natomiast, powinniśmy skorzystać z formuły a × b, w której a i b reprezentują długości odpowiednich boków.

Pole podstawy odgrywa kluczową rolę w całkowitym wzorze na pole powierzchni ostrosłupa, a także jest nieodzowne przy obliczaniu jego objętości. Zrozumienie tego konceptu jest szczególnie istotne w dziedzinach takich jak architektura czy inżynieria, gdzie precyzyjne obliczenia powierzchni pozwalają na efektywniejsze wykorzystanie materiałów budowlanych. Ponadto, ta wiedza przyczynia się do lepszego rozumienia geometrii przestrzennej oraz jej zastosowań w praktyce.

Jak obliczyć pole podstawy ostrosłupa?

Obliczanie pola podstawy ostrosłupa wymaga pewnego zrozumienia kształtu i długości boków podstawy. Dla kwadratowej podstawy posługujemy się prostym wzorem a², gdzie ‘a’ to długość boku. W przypadku prostokątów, pole obliczamy jako iloczyn długości dwóch boków, czyli a i b.

Gdy mamy do czynienia z innymi wielokątami, w grę wchodzą różne wzory geometryczne. Na przykład:

dla trójkątnej podstawy można złapać pole za pomocą wzoru (1/2) * a * h, gdzie ‘a’ to długość podstawy, a ‘h’ odpowiada wysokości trójkąta,
w przypadku wielokątów foremnych dostępne są specyficzne wzory dostosowane do ich kształtów.

W obliczeniach szczególne znaczenie mają kąty – zarówno prostokątne, jak i te występujące w trójkącie. Jest to kluczowe, zwłaszcza gdy podstawa ostrosłupa przyjmuje formę trójkąta lub innego złożonego wielokąta. Również długości boków odgrywają istotną rolę w precyzji obliczeń, a odpowiednie wzory geometryczne stanowią fundament analizy pola podstawy ostrosłupa, różniąc się w zależności od kształtu podstawy.

Jakie wzory stosuje się dla różnych kształtów podstawy?

Dla różnych kształtów podstaw ostrosłupa obowiązują odmienne wzory na obliczanie ich pól. Oto kilka przykładów:

w przypadku kwadratu: Pp = a², gdzie „a” to długość boku kwadratu,
w przypadku prostokąta: Pp = a × b, a „a” i „b” oznaczają długości jego boków,
w przypadku trójkąta: Pp = (a × h)/2, gdzie „a” to długość boku trójkąta, a „h” to jego wysokość,
w przypadku wielokątów foremnych: Pp = (n × a × apotema) / 2, gdzie „n” to liczba boków, „a” to długość boku, a apotema to odległość od środka wielokąta do jego krawędzi.

Zrozumienie tych wzorów ma kluczowe znaczenie, gdy przechodzimy do bardziej skomplikowanych obliczeń dotyczących całkowitej powierzchni oraz objętości ostrosłupa.

Jak długości boków i kąt prosty wpływają na pole podstawy?

Długości boków podstawy ostrosłupa odgrywają istotną rolę w obliczeniach pola tej podstawy. Ich wartości bezpośrednio wpływają na rezultaty. Na przykład, gdy chcemy wyznaczyć pole kwadratu, posługujemy się wzorem a², gdzie a oznacza długość boku. W przypadku prostokąta pole obliczamy według wzoru a × b, a a oraz b to długości odpowiednich boków. Kąt prosty, który między nimi występuje, jest kluczowy, ponieważ umożliwia wykorzystanie prostych równań matematycznych.

Jeżeli mówimy o trójkątach, kąt prosty oraz długości boków są niezbędne dla zastosowania funkcji trygonometrycznych oraz twierdzenia Pitagorasa. Te narzędzia pozwalają nam obliczyć wysokość trójkąta, co jest z kolei niezbędne do prawidłowego wyznaczenia jego pola. Zrozumienie kątów w trójkącie oraz długości jego boków skutkuje dokładnymi wynikami, które są niezwykle ważne w kolejnych obliczeniach związanych z ostrosłupami.

Jak wyliczyć pole powierzchni bocznej ostrosłupa?

Aby obliczyć pole powierzchni bocznej ostrosłupa, zaczynamy od ustalenia kształtu podstawy oraz wysokości ścian bocznych. Pole to, nazywane Pb, stanowi łączną sumę pól wszystkich trójkątnych ścian bocznych.

W przypadku ostrosłupa, którego podstawa ma kształt czworokąta, ściany boczne przyjmują formę trójkątów równoramiennych. Wzór na pole powierzchni bocznej dla tego typu ostrosłupa przedstawia się jako:

Pb = 2 * a * h, gdzie „a” oznacza długość krawędzi podstawy, a „h” to wysokość ściany bocznej. Dysponując tymi wymiarami, bez trudu możemy wyznaczyć pole powierzchni bocznej.

Kiedy mamy do czynienia z ostrosłupami o różnych rodzajach podstaw, konieczne staje się obliczenie:

pola każdego z bocznych trójkątów,
zsumowanie uzyskanych wyników.

W takich przypadkach warto sięgnąć po funkcje trygonometryczne oraz stosować odpowiednie wzory geometryczne. Na przykład, dla ostrosłupa o podstawie w kształcie trójkąta, pole boczne będzie obliczane w inny sposób, co wiąże się z koniecznością dostosowania metody do konkretnego kształtu podstawy.

Jak obliczać pole dla ostrosłupa prawidłowego czworokątnego?

Aby określić pole powierzchni ostrosłupa prawidłowego czworokątnego, który ma kwadratową podstawę o długości boku a, posługujemy się wzorem na całkowitą powierzchnię. Przedstawia się on w następujący sposób:

Pc = a² + 2 a h

W powyższym równaniu a² odnosi się do pola podstawy, a 2 a h przedstawia pole powierzchni bocznej. Ta część składa się z czterech równoramiennych trójkątów. Wysokość tych trójkątów, oznaczana jako h, można obliczyć wykorzystując funkcje trygonometryczne lub twierdzenie Pitagorasa, jeśli dysponujemy innymi wymiarami ostrosłupa.

Aby znaleźć pole powierzchni bocznej, stosujemy następujący wzór:

Pb = 2 a h

Krawędzie boczne łączą wierzchołek ostrosłupa z narożnikami podstawy, a ich długość ma kluczowy wpływ na pole powierzchni bocznej. Gdy znamy wysokość ściany bocznej, możemy także przeprowadzać dodatkowe obliczenia takie jak:

objętość,
inne właściwości geometryczne tego ostrosłupa.

Jak wyznaczyć wysokość ściany bocznej oraz krawędź boczną?

Aby ustalić wysokość bocznej ściany ostrosłupa, musisz znać dwa kluczowe elementy: kąt nachylenia tej ściany względem podstawy oraz długość krawędzi bocznej. Wysokość ściany bocznej (h) jest długością linii, która pozwala na obliczenie pola powierzchni bocznej. Do jej wyznaczenia przydatne będą funciones trygonometryczne. Na przykład, dla ostrosłupa z prostokątną podstawą, możesz użyć funkcji sinus kąta nachylenia i długości krawędzi podstawy.

Długość krawędzi bocznej, która łączy wierzchołek ostrosłupa z wierzchołkiem jego podstawy, można wyznaczyć dzięki twierdzeniu Pitagorasa. Wystarczy, że znasz rozmiary krawędzi podstawy oraz wysokość. Długość tej krawędzi obliczysz jako pierwiastek kwadratowy z sumy kwadratów długości podstawy i wysokości ściany bocznej. Na przykład, w przypadku ostrosłupa prawidłowego czworokątnego, równe długości krawędzi podstawy mają istotny wpływ na obliczenia wysokości, co czyni tę metodę niezwykle praktyczną do precyzyjnego określenia objętości oraz pola.

Kiedy można zastosować wzór Herona i funkcje trygonometryczne?

Wzór Herona oraz funkcje trygonometryczne są niezwykle ważne, gdy chodzi o ustalanie pola powierzchni bocznej ostrosłupa. Wykorzystując wzór Herona, z łatwością obliczamy pole trójkąta znając jedynie długości jego boków. To szczególnie pomocne w sytuacjach, gdy brakuje nam informacji o wysokości trójkąta, co często zdarza się podczas wyliczeń powierzchni bocznych ścian ostrosłupa. Wzór ten przyjmuje postać:

S = √(p(p-a)(p-b)(p-c)),

gdzie p to pół obwodu trójkąta, a a, b, c oznaczają długości jego boków.

Funkcje trygonometryczne również odgrywają istotną rolę, ułatwiając wyznaczanie wysokości ścian bocznych ostrosłupa oraz innych kluczowych wymiarów, gdy dysponujemy kątami i długościami boków. Na przykład, wysokość trójkąta może być obliczona z wykorzystaniem funkcji sinusowej, gdy znamy odpowiedni kąt oraz długości boków.

Obie z wymienionych metod mają fundamentalne znaczenie w geometrii przestrzennej, umożliwiając precyzyjne obliczenia zarówno powierzchni bocznej, jak i całkowitej ostrosłupa. Tego rodzaju kalkulacje są wyjątkowo cenne w dziedzinach takich jak architektura czy inżynieria.

Jak zsumować pole powierzchni całkowitej ostrosłupa?

Aby obliczyć całkowitą powierzchnię ostrosłupa, możemy posłużyć się prostym wzorem:

Pc = Pp + Pb.

W tej formule Pc oznacza pole całkowite, Pp to pole podstawy, natomiast Pb to powierzchnia boczna.

Aby znaleźć pole podstawy (Pp), musimy wziąć pod uwagę kształt, jaki ona ma. Na przykład, w przypadku prostokąta korzystamy z równania:

P = a × b,

gdzie a i b reprezentują długości boków.

Pole powierzchni bocznej (Pb) składa się przeważnie z pól trójkątnych, które tworzą ścianki ostrosłupa. Dla ostrosłupa prawidłowego czworokątnego, pole boczne obliczamy jako sumę pól czterech trójkątów. W tym wypadku do obliczeń wykorzystujemy wysokości ścian bocznych oraz długości krawędzi.

Kiedy przystępujemy do obliczenia całkowitej powierzchni ostrosłupa, warto pamiętać o doborze odpowiednich jednostek miary, w zależności od skali projektu. Na przykład, możemy używać:

metrów kwadratowych dla dużych konstrukcji,
centymetrów kwadratowych dla małych modeli.

Zsumowanie tych wartości daje nam precyzyjne określenie ilości materiału, który będzie potrzebny, co ma kluczowe znaczenie w praktycznych zastosowaniach budowlanych.

Jak wykorzystać wzór Pc = Pp + Pb?

Wzór Pc = Pp + Pb to kluczowe narzędzie w geometrii, które umożliwia wyznaczenie całkowitego pola powierzchni ostrosłupa. W tym równaniu Pc reprezentuje powierzchnię całkowitą, natomiast Pp i Pb to odpowiednio pole podstawy i pole powierzchni bocznej. Aby skutecznie z niego korzystać, warto kierować się kilkoma krokami:

Obliczenie pola podstawy (Pp). Kształt tej podstawy zdeterminuje, jaki wzór zastosujemy do obliczeń. Dla kwadratu będzie to Pp = a², podczas gdy dla trójkąta użyjemy Pp = (a * h) / 2, gdzie „a” to długość boku, a „h” oznacza wysokość.
Obliczanie pola powierzchni bocznej (Pb). To pole składa się z sumy pól wszystkich ścian bocznych. Każda ściana, jeśli jest trójkątem, ma swoje własne pole, które obliczamy na podstawie podobnych wzorów.
Dodanie wartości Pp i Pb. Gdy już zdobędziemy wartości Pp i Pb, wystarczy je dodać, aby uzyskać całkowite pole powierzchni (Pc). Dzięki temu równaniu możemy łatwo obliczyć powierzchnię ostrosłupa, niezależnie od jego kształtu czy liczby boków podstawy.
Zgodność jednostek miary. Pamiętajmy również o zgodności jednostek miary w trakcie obliczeń, gdyż ma to kluczowe znaczenie dla poprawności uzyskanych wyników.

Jakie jednostki miary stosować podczas obliczania powierzchni?

Podczas wyznaczania powierzchni ostrosłupa kluczowe jest stosowanie właściwych jednostek miary, co pozwala uzyskać dokładne wyniki. Najczęściej używane jednostki to:

centymetry kwadratowe (cm²),
metry kwadratowe (m²),
milimetry kwadratowe (mm²).

Ważne jest, aby wszystkie wymiary, jak długości krawędzi i wysokość ścian bocznych, były wyrażone w tych samych jednostkach. Dzięki temu unikniemy błędów w obliczeniach.

W praktycznych zastosowaniach, na przykład w budownictwie, precyzyjne określenie jednostek ma ogromne znaczenie. Dokładność przy obliczaniu ilości materiałów potrzebnych do pokrycia powierzchni ostrosłupa jest kluczowa. Jeśli obliczamy w metrach kwadratowych, wszystkie dane powinny być przeliczone na metry, co zapewnia jednolitość informacji. W przypadku mniejszych projektów, takich jak modele czy prototypy, centymetry kwadratowe mogą okazać się bardziej stosowne.

Przykłady i zadania z obliczania pola ostrosłupa

Przykłady i zadania związane z obliczaniem pola ostrosłupa są niezwykle istotne dla uczniów, zwłaszcza w szóstej klasie. Najczęściej koncentrują się oni na ostrosłupach prawidłowych, takich jak:

ostrosłupy o podstawie czworokątnej,
ostrosłupy o podstawie trójkątnej,
ostrosłupy o podstawie pięciokątnej.

Tego typu ćwiczenia można znaleźć w wielu podręcznikach do matematyki.

Zacznijmy od ostrosłupa prawidłowego czworokątnego, którego podstawa ma kształt kwadratu. Aby obliczyć pole całkowite tego ostrosłupa, konieczne jest dodanie pola jego podstawy (Pp) do pola powierzchni bocznej (Pb). Ten proces można zapisać równaniem Pc = Pp + Pb. Dla kwadratu o boku a, pole podstawy wynosi Pp = a². Natomiast pole powierzchni bocznej obliczamy jako Pb = 2 * a * h, gdzie h oznacza wysokość ścian bocznych.

Przechodząc do kolejnego przykładu, zajmijmy się ostrosłupem trójkątnym. W tym przypadku obliczenie pola podstawy można wykonać za pomocą wzoru Herona lub innych formuł stosowanych dla trójkątów. Aby ustalić pole boczne ostrosłupa trójkątnego, niekiedy konieczne okazuje się zastosowanie funkcji trygonometrycznych, co pozwala na wyznaczenie wysokości ścian bocznych w oparciu o kąty oraz długości boków trójkąta.

Możemy też rozważyć ostrosłup pięciokątny. Uczniowie mogą sięgać po wzory do obliczania pola podstawy oraz wykorzystywać twierdzenie Pitagorasa do określenia wysokości. Tego rodzaju zadania doskonale sprawdzają się jako materiał ćwiczeniowy na lekcjach matematyki, ponieważ pomagają w rozwijaniu umiejętności związanych z obliczaniem pól powierzchni ostrosłupów.

W szóstej klasie uczniowie często mają do czynienia z typowymi problemami matematycznymi, które umożliwiają im praktyczne zastosowanie nabytej wiedzy. Takie podejście ma kluczowe znaczenie dla rozwoju ich kompetencji geometrycznych oraz stanowi fundament do bardziej zaawansowanych zagadnień, które napotkają w przyszłości.

Obliczanie pola ostrosłupa prawidłowego czworokątnego (kwadrat w podstawie)

Aby obliczyć pole ostrosłupa prawidłowego czworokątnego, można skorzystać z formuły na całkowitą powierzchnię, której zapis wygląda następująco: Pc = a² + 2ah. W tym równaniu a reprezentuje długość krawędzi kwadratowej podstawy, natomiast h to wysokość bocznej ściany.

Obliczając pole podstawy (Pp), używamy formuły a², co a zarazem wskazuje na powierzchnię kwadratu. Następnie zajmujemy się polem powierzchni bocznej (Pb), które jest sumą pól czterech trójkątów równoramiennych. Dlatego wzór na to pole to Pb = 2ah.

Wysokość boku ściany (h) można znaleźć, stosując funkcje trygonometryczne lub przy użyciu twierdzenia Pitagorasa, o ile dysponujemy informacjami na temat innych długości boków ostrosłupa. W kontekście geometrii przestrzennej, podobne zagadnienia są powszechnie wykorzystywane w nauczaniu, dając uczniom praktyczne umiejętności obliczeniowe. Ostrosłupy tego typu mają także swoje miejsce w rzeczywistych problemach związanych z architekturą i projektowaniem, pokazując ich szerokie zastosowanie.

Obliczanie pola ostrosłupa trójkątnego i pięciokątnego

Obliczanie pola ostrosłupa trójkątnego wymaga znajomości pola jego podstawy oraz powierzchni bocznej. Pole podstawy, która przyjmuje kształt trójkąta, można wyznaczyć przy użyciu następującego wzoru:

Pp = (a × h) / 2

W tym równaniu „a” oznacza długość podstawy, a „h” to wysokość trójkąta. Następnie, by ustalić pole powierzchni bocznej, musimy zsumować pola trzech bocznych ścian, które również mają formę trójkątów. Całkowite pole powierzchni ostrosłupa trójkątnego można obliczyć według wzoru:

Pc = Pp + Pb

Tutaj „Pb” to suma powierzchni trzech ścian bocznych.

Gdy przechodzimy do ostrosłupa pięciokątnego, jego podstawa staje się pięciokątem foremnym. Obliczenie pola podstawy wymaga uwzględnienia liczby boków „n” oraz długości boku „a” i apotemy „p”:

Pp = (1/2) × n × a × p

Powierzchnia pięciu bocznych trójkątów tworzy pole powierzchni bocznej, które znowu działa na podobnej zasadzie jak w przypadku ostrosłupa trójkątnego. Całkowitą powierzchnię można obliczyć, korzystając z tego samego wzoru:

Pc = Pp + Pb

W dodatkowych obliczeniach pomocne mogą być wzór Herona oraz funkcje trygonometryczne, dzięki którym można określić wysokości oraz kąty. Dzięki tym narzędziom uzyskujemy precyzyjne wymiary zarówno ostrosłupa trójkątnego, jak i pięciokątnego.

Typowe zadania szkolne, klasa VI

Typowe zadania, które uczniowie klasy VI rozwiązują w związku z ostrosłupami, stają się fascynującym wyzwaniem matematycznym. Kluczowe aspekty tych zadań obejmują obliczanie zarówno pola powierzchni całkowitej, jak i bocznej, a także ustalanie długości krawędzi oraz wysokości ścian bocznych. W trakcie pracy nad nimi, uczniowie mają okazję skorzystać z twierdzenia Pitagorasa, funkcji trygonometrycznych oraz wzoru Herona, co znacząco rozwija ich umiejętności geometryczne.

Na przykład niektóre zadania mogą obejmować:

obliczenie pola powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, uczniowie muszą zrozumieć, jak określić pole podstawy oraz pole powierzchni bocznej, a następnie umiejętnie zsumować te wartości przy użyciu odpowiedniego wzoru,
rozwiązywanie zadań związanych z ostrosłupami o trójkątnych i pięciokątnych podstawach, przy takich obliczeniach uczniowie uczą się dostosowywać używane wzory do różnorodnych kształtów podstaw, co korzystnie wpływa na ich zdolności analityczne,
wykorzystanie wzoru Herona do obliczania pól powierzchni trójkątów, które stanowią boki ostrosłupa, dzięki temu wzorowi, nawet skomplikowane długości boków stają się łatwiejsze do obliczenia.

Te zadania nie tylko przygotowują uczniów na bardziej zaawansowane tematy matematyczne, ale także angażują ich w rozwój umiejętności analizy i rozwiązywania problemów.

Gdzie wykorzystuje się wzór na pole ostrosłupa?

Wzór na pole ostrosłupa odgrywa ważną rolę w wielu dziedzinach, zwłaszcza w architekturze i budownictwie. Umożliwia dokładne obliczenie powierzchni, którą należy pokryć materiałami budowlanymi, co stanowi istotny etap w planowaniu i realizacji różnorodnych projektów.

W praktyce wykorzystanie tego wzoru przyczynia się do:

lepszej optymalizacji przestrzeni,
efektywnego zarządzania dostępnymi zasobami,
ułatwienia doboru odpowiednich materiałów budowlanych,
redukcji kosztów,
zwiększenia efektywności energetycznej budynków.

Dodatkowo, inżynierowie i architekci polegają na tym wzorze, aby zminimalizować marnotrawstwo materiałów. Starannie zaplanowane rozmieszczenie elementów konstrukcyjnych jest kluczowe w każdej inwestycji budowlanej. Wzór na pole ostrosłupa stanowi nie tylko narzędzie matematyczne, ale również praktyczne wsparcie w pracach budowlanych oraz architektonicznych.

Zastosowania praktyczne w architekturze i konstrukcjach budowlanych

W architekturze i budownictwie wzór na pole ostrosłupa odgrywa kluczową rolę. Dzięki niemu architekci i inżynierowie mogą z łatwością planować i realizować swoje projekty, umożliwiając im obliczenie powierzchni ostrosłupa, co jest niezbędne do oszacowania ilości materiałów potrzebnych na pokrycia dachowe, ściany czy inne elementy konstrukcyjne, co wpływa na ostateczne koszty i umożliwia lepszą optymalizację procesów budowlanych.

Formuła ta pozwala na kalkulację zarówno całkowitej, jak i bocznej powierzchni ostrosłupa, co ma ogromne znaczenie dla estetyki oraz funkcjonalności budynków. Na przykład, wcześniejsze ustalenie powierzchni, która ma być pokryta, ułatwia zaplanowanie użycia różnych materiałów, takich jak:

blacha,
szkło,
beton.

Takie podejście sprzyja wprowadzeniu bardziej zrównoważonych rozwiązań w budownictwie.

Dodatkowo, cechy ostrosłupów, w tym ich stabilność oraz wytrzymałość, są niezwykle istotne podczas projektowania nowoczesnych obiektów. W dzisiejszych czasach architekci chętnie sięgają po nietypowe kształty i formy. Przykładem mogą być innowacyjne konstrukcje stalowe, budynki mieszkalne oraz przestrzenie publiczne. Stosowanie oryginalnych form ostrosłupowych nie tylko poprawia estetykę architektoniczną, ale też zwiększa efektywność energetyczną budynków.

Nie ma wątpliwości, że umiejętność korzystania z wzoru na pole ostrosłupa jest nieodzownym elementem współczesnych praktyk budowlanych. Dzięki temu można tworzyć więcej funkcjonalnych, nowoczesnych i atrakcyjnych przestrzeni.

Jak wzór pomaga w optymalizacji przestrzeni i doborze materiałów?

Wzór na pole ostrosłupa odgrywa kluczową rolę w architekturze oraz budownictwie. Umożliwia dokładne obliczenia powierzchni, co jest nieocenione w pracy projektantów i inżynierów. Efektywna optymalizacja przestrzeni, wynikająca z tych obliczeń, pozwala na zmniejszenie strat materiałowych, a tym samym prowadzi do obniżenia kosztów budowy.

Warto zrozumieć, jakie różnice zachodzą między polem powierzchni całkowitej a bocznej, gdyż ma to bezpośredni wpływ na zapotrzebowanie na materiały budowlane. Odpowiedni dobór tych komponentów, bazujący na wynikach obliczeń, sprzyja tworzeniu funkcjonalnych i ekonomicznych projektów. Dobrze zaplanowane użycie powierzchni maksymalizuje dostępne zasoby, co jest szczególnie istotne w zatłoczonych obszarach miejskich.

W praktyce, znajomość wzoru na pole ostrosłupa oraz jego właściwości geometrycznych pozwala architektom i inżynierom na skuteczne planowanie budowli. Na przykład, wybór technologii budowlanych jest ściśle związany z wymaganiami dotyczącymi materiałów. Informacje te można uzyskać właśnie dzięki analizie powierzchni. W rezultacie, zastosowanie wzoru przyczynia się do lepszego zarządzania zasobami, co ma kluczowe znaczenie w nowoczesnym budownictwie.