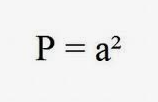Pole kwadratu wyliczamy, podnosząc do kwadratu długość jego boku. Wzór przedstawia się jako P = a², gdzie a to długość jednego z boków. Ten prosty sposób pozwala łatwo obliczyć powierzchnię, mając tylko jedną miarę boku. Kwadrat charakteryzuje się równymi bokami oraz kątem prostym, co sprawia, że jego pole można wykorzystywać w różnych działach matematyki oraz zastosowaniach praktycznych.
Czym jest kwadrat jako figura geometryczna?
Kwadrat to czworokąt o równych bokach, w którym wszystkie kąty wewnętrzne są równe i mają po 90 stopni. Można go traktować jako szczególny przypadek prostokąta, który jednocześnie posiada właściwości rombu. Dzięki temu kwadrat wyróżnia się wyjątkową symetrią spośród figur geometrycznych.
Jakie są właściwości kwadratu w kontekście pola?
Pole kwadratu to miara przestrzeni zajmowanej przez tę figurę, w której wszystkie boki mają identyczną długość. Aby obliczyć jego powierzchnię, wystarczy skorzystać ze wzoru P = a², gdzie „a” oznacza długość boku.
Ciekawostką jest, że:
- przekątne kwadratu są równej długości,
- przekątne przecinają się w swoim środku,
- przekątne tworzą kąt prosty.
- dzielimy kwadrat na dwa identyczne trójkąty prostokątne,
- stosujemy twierdzenie Pitagorasa do obliczenia długości przekątnej.
Możemy to wyrazić wzorem d = a√2. Ta sama formuła daje nam także możliwość obliczenia pola kwadratu, wykorzystując przekątną, a wzór na to brzmi P = (1/2)d².
Warto zauważyć, że pole kwadratu jest wyrażane w jednostkach kwadratowych, takich jak cm² lub m². Taki sposób oznaczania wynika z konieczności uwzględnienia obu wymiarów powierzchni.
Jak bok i przekątna wpływają na pole kwadratu?
Bok kwadratu, który symbolizujemy literą „a”, ma ogromne znaczenie dla obliczenia jego powierzchni. Można to łatwo zauważyć w formule P = a², co oznacza, że pole kwadratu jest równe kwadratowi długości jego boku. Kiedy wydłużamy bok, jego pole zwiększa się w sposób proporcjonalny do kwadratu tej zmiany.
Dodatkowo, przekątna kwadratu, zazwyczaj określana jako „d”, również odgrywa istotną rolę w obliczeniach dotyczących powierzchni. W tym przypadku posługujemy się wzorem P = d²/2. Możemy zauważyć, że długość przekątnej wiąże się z bokiem poprzez zależność d = a√2, która opiera się na twierdzeniu Pitagorasa. Dzięki temu, jeśli znamy długość przekątnej, bez trwoniącego czasu możemy wyznaczyć pole, nawet w sytuacji, gdy długość boku jest nam nieznana.
Jak obwód kwadratu wiąże się z polem?
Obwód kwadratu to po prostu suma długości jego czterech równych boków. Możemy to wyrazić za pomocą prostego wzoru: O = 4a, gdzie 'a’ oznacza długość boku. Gdy już wiemy, jaki jest obwód, łatwo możemy wyznaczyć długość boku – wystarczy podzielić obwód przez cztery (a = O/4).
Jeśli chodzi o pole kwadratu, obliczamy je korzystając z wzoru P = a². Co ciekawe, pole można również zdefiniować za pomocą obwodu, co prowadzi nas do wzoru P = (O/4)². Na przykład, jeśli obwód wynosi 24 cm, to każdy bok ma długość 6 cm, a jego pole wynosi 36 cm².
Dzięki tej zależności możemy szybko obliczyć pole kwadratu, mając tylko informację o obwodzie, bez potrzeby wiedzy o długości boków.
| Parametr | Wzór | Opis |
|---|---|---|
| Pole kwadratu (bok) | P = a² | Pole wyrażone jako kwadrat długości boku a |
| Pole kwadratu (przekątna) | P = d² / 2 | Pole wyrażone za pomocą przekątnej d |
| Długość przekątnej | d = a√2 | Przekątna kwadratu jako funkcja długości boku |
| Długość boku (z pola) | a = √P | Bok kwadratu wyliczony z pola |
| Długość boku (z przekątnej) | a = d / √2 | Bok kwadratu wyliczony z przekątnej |
| Obwód kwadratu | O = 4a | Suma długości czterech boków |
| Bok kwadratu (z obwodu) | a = O / 4 | Długość boku wyliczona z obwodu |
| Pole kwadratu (z obwodu) | P = (O / 4)² | Pole wyliczone korzystając z obwodu |
| Jednostki pola | cm², m², km², ha, a | Jednostki wyrażające dwuwymiarową powierzchnię |
| Przeliczniki jednostek |
1 m² = 10 000 cm² 1 km² = 1 000 000 m² 1 dm² = 100 cm² 1 a = 100 m² 1 ha = 10 000 m² | Konwersje pomiędzy jednostkami pola |
| Zależność Pitagorasa | d² = 2a² | Relacja między przekątną a bokiem kwadratu |
Jaki jest podstawowy wzór na pole kwadratu?
Podstawowy wzór do obliczenia pola kwadratu to P = a². W tym równaniu 'P’ reprezentuje pole, a 'a’ oznacza długość boku. Ale dlaczego tak to działa? Kwadrat charakteryzuje się czterema równymi bokami i kątami prostymi, a jego pole to przestrzeń, którą zajmuje figura o wymiarach a na a.
Aby dowiedzieć się, jakie jest pole, wystarczy pomnożyć długość jednego boku przez siebie. To bardzo łatwy krok. Ten wzór jest niezwykle istotny w matematyce oraz geometrii, ponieważ umożliwia szybkie i precyzyjne obliczenia powierzchni kwadratu.
Jednostką, w której podajemy pole, jest zawsze jednostka kwadratowa, na przykład:
- centymetry kwadratowe (cm²),
- metry kwadratowe (m²).
Warto również wspomnieć o alternatywnym wzorze. Gdy znamy długość przekątnej, oznaczanej literą d, możemy skorzystać z wzoru P = d²/2.
Jak działa wzór P = a²?
Wzór P = a² wskazuje, jak obliczyć pole kwadratu, podnosząc długość boku 'a’ do kwadratu. Innymi słowy, pole kwadratu uzyskujemy, mnożąc długość boku przez siebie. Ta metoda obliczania ma sens, ponieważ kwadrat istnieje w dwóch wymiarach, co wymaga pomnożenia długości w obu kierunkach, aby uzyskać całkowitą powierzchnię.
W praktyce, gdy znamy długość boku, wystarczy przeprowadzić jedno proste działanie matematyczne. Dzięki temu wzór ten staje się wygodnym i skutecznym narzędziem do określania pola kwadratu w różnych jednostkach miary.
Dlaczego pole wyraża się w jednostkach kwadratowych?
Pole wyrażane jest w jednostkach kwadratowych, ponieważ odnosi się do dwuwymiarowej powierzchni, którą zajmuje figura, a nie do długości linii. Do jednostek pola zaliczamy długości podniesione do kwadratu, takie jak:
- centymetr kwadratowy (cm²),
- metr kwadratowy (m²),
- kilometr kwadratowy (km²).
Na przykład pole kwadratu o boku 1 metra wynosi 1 m². Oznacza to, że powierzchnia kwadratu o wymiarach 1 m × 1 m równa się 1 m². Taki sposób wyrażania jednostek umożliwia dokładne określenie rozmiaru powierzchni oraz zapewnia spójność w obliczeniach.
Jak obliczyć pole kwadratu przy podanej długości boku?
Aby obliczyć pole kwadratu, wystarczy znać długość jego boku oznaczoną jako ’a’. Wykorzystujemy do tego prosty wzór: P = a². Innymi słowy, musisz pomnożyć długość boku przez siebie. Przykładowo, jeśli bok ma 7 cm, pole wyniesie 7 cm × 7 cm, co daje 49 cm².
Pamiętaj, że długość boku powinna być wyrażona w miarach takich jak:
- centymetry (cm),
- metry (m),
- milimetry (mm).
Rezultat obliczeń zawsze przedstawiaj w odpowiednich jednostkach kwadratowych, czyli cm², m² czy mm².
Obliczanie powierzchni kwadratu jest naprawdę szybkie i nieskomplikowane dzięki temu wzorowi. Ważne jest, by przy obliczeniach korzystać z tych samych jednostek długości, co pomoże uniknąć ewentualnych nieporozumień.
Na przykład, gdy długość boku wynosi 0,5 m, obliczamy pole jako 0,5 × 0,5, co daje 0,25 m². Dzięki temu bez trwonić czas, możesz z łatwością obliczyć pole kwadratu niezależnie od jego rozmiaru.
Jak przeliczać pole kwadratu na różne jednostki (cm², m², km²)?
Przeliczanie pól kwadratowych pomiędzy różnymi jednostkami wymaga podniesienia przelicznika długości do kwadratu. Na przykład, aby przeprowadzić konwersję pola z centymetrów kwadratowych (cm²) na metry kwadratowe (m²), wystarczy podzielić wartość przez 10 000, ponieważ 1 metr to 100 centymetrów, a gdy podniesiemy 100 do kwadratu, otrzymujemy 10 000.
W podobny sposób, 1 km² równa się 1 000 000 m². Wynika to z faktu, że 1 kilometr to 1000 metrów, a podnosząc 1000 do kwadratu, dostajemy 1 000 000.
Oto kilka istotnych przeliczników, które mogą być pomocne:
- 1 m² to 10 000 cm²,
- 1 km² z kolei to 1 000 000 m²,
- 1 dm² można przeliczyć na 100 cm²,
- 1 a odpowiada 100 m²,
- 1 ha to 10 000 m².
Gdy chcemy przeliczyć pole kwadratu z cm² na m², wystarczy podzielić przez 10 000. Natomiast, gdy dokonujemy konwersji z m² na cm², działamy w przeciwnym kierunku i mnożymy przez 10 000. Jeśli zaś planujemy zamienić m² na km², dzielimy przez 1 000 000.
Warto pamiętać, że jednostki pola zawsze wyrażają się w formie kwadratowej. Dlatego, podejmując się przeliczania, nie możemy zapomnieć o uwzględnieniu kwadratu przelicznika długości.
Jak obliczyć pole kwadratu mając długość przekątnej?
Aby obliczyć pole kwadratu mając długość jego przekątnej (d), możemy zastosować prosty wzór: P = d² / 2. W tym przypadku bazujemy na zależności między bokiem a przekątną kwadratu, którą można określić równaniem d = a√2. Gdy podstawimy a = d/√2 do wzoru na pole kwadratu P = a², otrzymujemy P = (d/√2)². Tak więc, pole kwadratu można wyrazić jako połowę kwadratu długości przekątnej.Aby przeprowadzić obliczenia pola kwadratu na podstawie długości przekątnej, warto postępować według następujących kroków:
- zmierz długość przekątnej d,
- oblicz d², czyli podnieś długość przekątnej do kwadratu,
- podziel d² przez 2, aby uzyskać wartość pola kwadratu.
Na przykład, jeśli mamy przekątną o długości 8 cm, nasze obliczenia wyglądają następująco: P = 64 / 2 = 32 cm².Warto dodać, że do uzyskania tego wzoru wykorzystujemy twierdzenie Pitagorasa. Przekątna kwadratu dzieli go na dwa trójkąty prostokątne, w których przekątna pełni rolę przeciwprostokątnej, a boki stanowią przyprostokątne. Tak się składa, że dzięki temu łatwo możemy przeliczyć długość przekątnej na długość boku i obliczyć pole kwadratu.
Jak stosować wzór P = d²/2?
Wzór P = d²/2 jest użyteczny, gdy mamy do czynienia z długością przekątnej kwadratu. Aby rozpocząć, wykonaj następujące kroki:
- zmierz długość tej przekątnej (d),
- podnieś ją do kwadratu (d²),
- podziel przez 2.
Wynik, który uzyskasz, to pole kwadratu, a jego jednostki będą zgodne z długością przekątnej. Wartości te są oparte na twierdzeniu Pitagorasa, które łączy bok kwadratu z długością jego przekątnej. To wygodna i efektywna metoda obliczania pola kwadratu, a znajomość tego wzoru na pewno się przyda.
Jak długość przekątnej oblicza się z boku kwadratu?
Długość przekątnej kwadratu można łatwo ustalić, stosując wzór d = a√2. W tym równaniu 'a’ symbolizuje długość jednego z boków kwadratu. Związek ten wynika z twierdzenia Pitagorasa. Przekątna stanowi przeciwprostokątną w trójkącie prostokątnym, którego boki odpowiadają bokom kwadratu.Na przykład, gdy długość boku kwadratu wynosi 5 cm, obliczamy przekątną jako 5 cm pomnożone przez √2, co daje w przybliżeniu 7,07 cm. Znajomość tego wzoru jest niezwykle pomocna przy rozwiązywaniu różnych zadań geometrycznych, umożliwiając szybkie przeliczenie długości przekątnej na długość boku i odwrotnie.
Jak twierdzenie Pitagorasa pomaga znaleźć pole?
Twierdzenie Pitagorasa znajduje szerokie zastosowanie w obliczeniach związanych z polem kwadratu, zwłaszcza gdy dysponujemy długością jego przekątnej. Ta przekątna dzieli kwadrat na dwa identyczne trójkąty prostokątne, w których długości przyprostokątnych odpowiadają długościom boków kwadratu.
Z tego zasady możemy wywnioskować równanie: d² = 2a², gdzie d oznacza długość przekątnej, a a to długość boku kwadratu. Dzięki temu możemy łatwo określić długość boku za pomocą wzoru a = d/√2.
Aby obliczyć pole kwadratu, korzystamy z równania P = a². Po zastąpieniu a² równaniem d²/2, otrzymujemy formułę na pole w zależności od długości przekątnej: P = d²/2.
Te proste obliczenia sprawiają, że twierdzenie Pitagorasa jest niezwykle pomocne w znajdowaniu pola kwadratu na podstawie długości jego przekątnej, co bywa szczególnie korzystne, gdy pomiar boków kwadratu staje się utrudniony.
Jak wyznaczyć bok kwadratu na podstawie pola lub przekątnej?
Aby obliczyć długość boku kwadratu na podstawie jego pola, można zastosować prosty wzór: a = √P, gdzie P reprezentuje pole kwadratu. Na przykład, gdy pole wynosi 64 cm², długość boku możemy łatwo wyliczyć jako √64, co daje nam 8 cm.
Inny sposób na ustalenie długości boku polega na znaniu długości przekątnej (d). W takim przypadku stosujemy wzór: a = d/√2. Jeśli przekątna ma 14 cm, bok kwadratu obliczymy dzieląc 14 przez 1,414, co daje nam w przybliżeniu 9,9 cm.
Te proste wzory umożliwiają szybką i precyzyjną kalkulację długości boku kwadratu, w zależności od dostępnych danych geometrycznych.