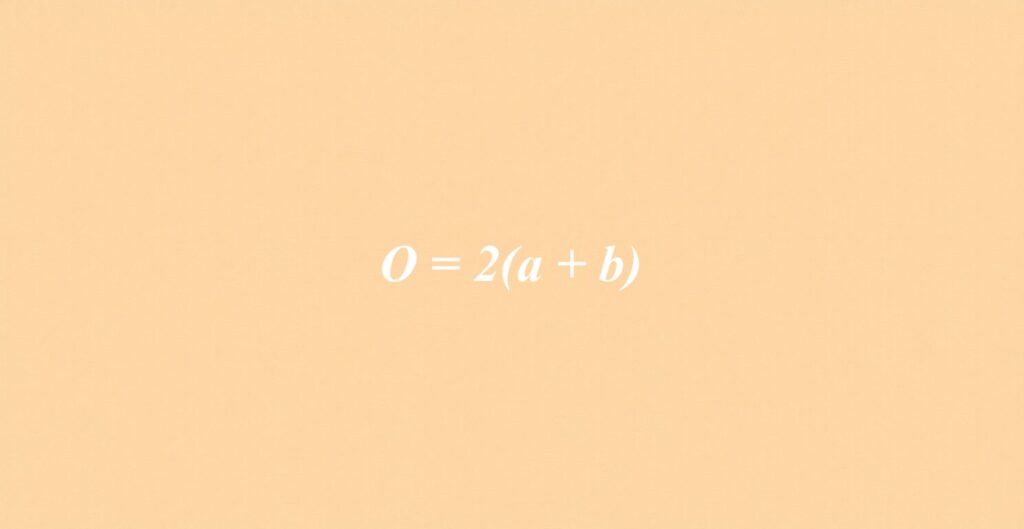Wzór na obwód prostokąta

Co to jest obwód prostokąta?

Obwód prostokąta to całkowita długość, którą trzeba pokonać, aby obejść tę figurę. Aby go obliczyć, wystarczy dodać długości wszystkich boków prostokąta. Można to zapisać za pomocą wzoru O = 2(a + b), gdzie „a” i „b” oznaczają długości boków. Prostokąt to specyficzny typ czworokąta, który charakteryzuje się dwiema parami równoległych boków oraz tym, że przeciwległe boki mają identyczną długość.

Pomiar obwodu prostokąta można przeprowadzać w różnych jednostkach, takich jak:

• centymetry,
• metry,
• milimetry.

To fundamentalna koncepcja w matematyce oraz geometrii.

Zrozumienie obwodu prostokąta jest niezwykle istotne w licznych dziedzinach, w tym w:

• architekturze,
• budownictwie,
• planowaniu przestrzennym.

Wiedza na temat obliczania obwodu pozwala lepiej pojąć proporcje figur, a także może być przydatna na przykład przy ustalaniu długości ogrodzeń czy projektowaniu wnętrz.

Jak działa wzór na obwód prostokąta?

Wzór na obwód prostokąta można wyrazić jako O = 2(a + b), gdzie a i b reprezentują długości dwóch obok siebie znajdujących się boków. Obliczenie obwodu przy użyciu tego wzoru jest proste i dostarcza błyskawicznych rezultatów, co ma ogromne znaczenie w różnych praktycznych zastosowaniach, takich jak:

• projektowanie budynków,
• budowa ogrodzeń,
• tworzenie planów architektonicznych.

Kluczowym założeniem tego wzoru jest fakt, że prostokąt ma dwie pary równoległych boków. Aby uzyskać całkowity obwód, wystarczy zsumować długości obu boków i pomnożyć je przez dwa, co pozwala uniknąć skomplikowanych obliczeń, a także skupić się na bardziej praktycznych zadaniach, takich jak:

• rysowanie prostokątów,
• przeprowadzanie podobnych kalkulacji,
• uzyskiwanie dokładnych wyników.

Zrozumienie wzoru O = 2(a + b) jest kluczowe, zwłaszcza gdy dokonujemy pomiarów związanych z prostokątami. Ta wiedza umożliwia również korzystanie z różnych narzędzi do szybkiego obliczania obwodu w rozmaitych sytuacjach, co jest niezwykle istotne zarówno w matematyce, jak i w wielu dziedzinach codziennego życia.

Jak wygląda wzór O = 2(a + b)?

Wzór na obwód prostokąta, O = 2(a + b), stanowi prosty sposób na obliczenie jego długości. Tutaj O oznacza obwód, a litery a i b odnoszą się do długości boków. Aby ustalić obwód, wystarczy zsumować długości dwóch sąsiednich boków i pomnożyć uzyskaną wartość przez 2.

Korzystając z tej formuły, łatwo wyznaczymy obwód prostokąta w dowolnych jednostkach miary. Dla przykładu:

• jeśli a wynosi 3 cm,
• a b to 4 cm,

obliczenie obwodu wygląda następująco: O = 2(3 + 4) = 2 × 7 = 14 cm. Takie obliczenia mają praktyczne zastosowanie, na przykład przy mierzeniu powierzchni ogrodów czy wnętrz, gdzie znajomość obwodu jest niezbędna.

Jakie znaczenie mają długości boków a i b?

Długości boków prostokąta, oznaczane jako a i b, mają zasadnicze znaczenie w różnych obliczeniach związanych z tym kształtem geometrycznym. W szczególności, wpływają one na obwód, który można obliczyć za pomocą prostego wzoru O = 2(a + b). Warto zauważyć, że im większe są te dwa wymiary, tym większa staje się długość obwodu prostokąta.

Oprócz tego, wartości a i b są niezbędne do wyznaczenia pola prostokąta, co można zrobić stosując wzór P = a * b. To kluczowy aspekt, zwłaszcza dla architektów, którzy muszą dokładnie planować wykorzystanie przestrzeni w swoich projektach.

Długości boków pozwalają również na obliczenie przekątnej prostokąta, co realizuje się poprzez zastosowanie twierdzenia Pitagorasa. Ta wiedza jest użyteczna w licznych sytuacjach, takich jak:

• rysowanie prostokąta,
• dokonanie precyzyjnych pomiarów.

Warto podkreślić, że precyzyjne określenie wartości a i b ma ogromne znaczenie; nawet niewielkie błędy w tych obliczeniach mogą skutkować niepoprawnymi wynikami.

Jak obliczyć obwód prostokąta krok po kroku?

Aby obliczyć obwód prostokąta, warto wykonać kilka prostych kroków:

1. zmierz długości sąsiadujących boków, które oznaczymy jako a i b,
2. dodaj długości boków a i b,
3. skorzystaj z wzoru na obwód: O = 2(a + b),
4. pomnóż uzyskaną sumę przez 2,
5. pamiętaj, aby wynik był w tych samych jednostkach, w których dokonano pomiarów.

Dzięki temu bierzesz pod uwagę wszystkie cztery boki prostokąta. Możesz również skorzystać z różnych narzędzi online, takich jak kalkulatory obwodu, które mogą uprościć cały proces i zminimalizować ryzyko pomyłek.

Jak poprawnie wyznaczać długości boków prostokąta?

Aby skutecznie określić długości boków prostokąta, warto skorzystać z różnych narzędzi pomiarowych, takich jak linijka czy taśma miernicza. Proces rozpoczynamy od zmierzenia dwóch sąsiadujących krawędzi, które nazywamy „a” oraz „b”. Istotne jest, aby wszystkie pomiary odbywały się w tej samej jednostce, co jest kluczem do precyzyjnych obliczeń obwodu i pola prostokąta.

Podczas dokonywania pomiarów pamiętaj, by mierzyć wzdłuż prostych krawędzi, co podnosi precyzję wyników. Jakość pomiarów ma ogromne znaczenie dla dalszych obliczeń i ich zastosowań w praktyce. Jeśli posługujesz się niestandardowymi jednostkami, konieczna będzie ich konwersja, aby precyzyjnie określić długości boków.

Aby zminimalizować ryzyko błędów, warto sięgnąć po cyfrowe narzędzia pomiarowe, które zapewniają większą dokładność. Ponadto, zaleca się na bieżąco zapisywać dokonane pomiary, co znacznie ułatwia późniejsze obliczenia. Staranność podczas mierzenia to podstawa dla prawidłowego działania prostokąta i jego zastosowania w praktyce.

Jakie jednostki miary stosuje się przy obwodzie?

Obliczanie obwodu prostokąta to zadanie, które wymaga znajomości jednostek miary. Ponieważ obwód określa długość, kluczowe jest, aby wszystkie wymiary boków były wyrażone w tych samych jednostkach, co zapewni dokładność obliczeń.

Do najczęściej stosowanych jednostek należą:

• Centymetry (cm) – często wykorzystywane w codziennych czynnościach, zwłaszcza w kontekście edukacyjnym,
• Metry (m) – uznawane za standardową jednostkę długości, idealną do większych projektów, takich jak budowy,
• Decymetry (dm) – stanowią praktyczne rozwiązanie, gdy potrzebujemy czegoś pomiędzy centymetrami a metrami,
• Milimetry (mm) – doskonałe w sytuacjach wymagających precyzyjnych pomiarów, na przykład w rzemiośle czy inżynierii.

Wybór odpowiedniej jednostki zależy od wymiarów prostokąta oraz kontekstu, w jakim ma być używany. Ważne jest także stosowanie spójnych jednostek, aby uzyskać prawidłowy wynik.

Przykłady obliczania obwodu prostokąta

Aby zobaczyć, w jaki sposób obliczamy obwód prostokąta, warto przyjrzeć się kilku różnym przykładom. Dzięki nim lepiej zrozumiemy, jak zastosować wzór O = 2(a + b).

1. Przykład 1: prostokąt o wymiarach a = 5 cm i b = 7 cm, obliczenie obwodu: O = 2(5 cm + 7 cm) = 2(12 cm) = 24 cm,
2. Przykład 2: prostokąt o bokach a = 8 m i b = 3 m, obliczenie obwodu: O = 2(8 m + 3 m) = 2(11 m) = 22 m,
3. Przykład 3: prostokąt o długościach a = 2,5 stopy oraz b = 1,5 stopy, obliczenie obwodu: O = 2(2,5 ft + 1,5 ft) = 2(4 ft) = 8 ft.

Różnorodne przykłady z różnymi długościami boków i jednostkami miary mogą w znaczny sposób ułatwić zrozumienie, jak korzystać ze wzoru w codziennym życiu. Na przykład, przy planowaniu przestrzeni czy w budownictwie, te obliczenia stają się niezwykle pomocne.

Jak obliczyć obwód z podanymi bokami?

Aby wyznaczyć obwód prostokąta, wystarczy skorzystać z prostego wzoru: O = 2(a + b). W tym równaniu „a” i „b” oznaczają długości dwóch sąsiednich boków prostokąta. Sam proces obliczeń jest intuicyjny i nieskomplikowany.

Na przykład, gdy bok „a” ma długość 8 cm, a bok „b” wynosi 3 cm, obliczenia odbywają się w następujący sposób:

1. najpierw sumujemy długości boków: 8 cm + 3 cm = 11 cm,
2. następnie mnożymy otrzymaną sumę przez 2: 2 × 11 cm = 22 cm.

W efekcie otrzymujemy obwód prostokąta równy 22 cm. Kluczowe jest, aby długości obu boków były podane w tej samej jednostce miary, co zapewni spójność wyników. Dodatkowo warto upewnić się, czy operujemy w centymetrach czy metrach, aby uniknąć pomyłek. Umiejętność obliczania obwodu prostokąta znajduje zastosowanie w wielu praktycznych sytuacjach, jak na przykład przy planowaniu ogrodzeń czy aranżowaniu wnętrz.

Jak wykorzystać wzór przy nietypowych jednostkach?

Aby obliczyć obwód prostokąta, używamy prostego wzoru O = 2(a + b). Kiedy pracujemy z nietypowymi jednostkami, takimi jak cale, stopy czy jardy, niezwykle istotne jest, aby oba wymiary – a oraz b – były wyrażone w tej samej jednostce. Choć wzór pozostaje niezmieniony, precyzja obliczeń w dużej mierze zależy od konsekwencji w doborze jednostek.

Na przykład, jeśli jeden bok, a, jest w stopach, a bok b w calach, konieczne będzie przeliczenie jednego z wymiarów na pasującą jednostkę. W praktyce korzystanie z kalkulatorów obwodu lub różnorodnych narzędzi obliczeniowych znacząco ułatwia ten proces. Wiele z tych aplikacji automatycznie konwertuje jednostki, co pozwala nam szybko i precyzyjnie uzyskać wyniki bez potrzeby ręcznego przeliczania.

Dodatkowo, korzystanie z kalkulatorów podnosi dokładność wyników, minimalizując ryzyko błędów, które mogą wyniknąć z nieprawidłowej konwersji jednostek. Zastosowanie wzoru na obwód prostokąta w kontekście różnych jednostek jest istotne w wielu dziedzinach, takich jak architektura czy projektowanie wnętrz, gdzie precyzyjne pomiary odgrywają kluczową rolę.

Jak wykorzystać kalkulator obwodu prostokąta?

Kalkulator obwodu prostokąta to niezwykle pomocne narzędzie, które znacznie ułatwia wykonywanie obliczeń. Użytkownicy mogą błyskawicznie wprowadzić długości dwóch boków prostokąta. Następnie kalkulator automatycznie wykorzystuje wzór O = 2(a + b) do obliczenia wyniku. Takie aplikacje są szczególnie istotne w dziedzinach takich jak:

• edukacja,
• architektura,
• inżynieria.

W tych obszarach precyzja obliczeń odgrywa kluczową rolę.

Aby skorzystać z kalkulatora, wystarczy wprowadzić wartości dla boków a i b. Po wpisaniu danych, kalkulator szybko generuje wynik, co znacznie zmniejsza ryzyko popełnienia błędów, które mogą się zdarzyć przy obliczeniach ręcznych. Wiele z tych narzędzi oferuje też możliwość konwersji jednostek, co jest szczególnie użyteczne, gdy długości są podawane w różnych systemach miar.

Ponadto, nowoczesne kalkulatory umożliwiają także wizualizację prostokątów o określonym obwodzie. Takie funkcje są niezwykle przydatne zarówno w projektach architektonicznych, jak i podczas lekcji matematyki. Dzięki nim użytkownicy mogą:

• łatwiej zrozumieć omawiane zagadnienia,
• wizualizować wyniki.

Warto skorzystać z kalkulatora obwodu, aby uprościć proces obliczeń i zaoszczędzić cenny czas.

Przykłady praktycznego zastosowania obwodu prostokąta

Obwód prostokąta zyskuje zastosowanie w wielu obszarach, takich jak architektura czy ogrodnictwo. Zrozumienie, jak obliczyć ten obwód, odgrywa istotną rolę w projektowaniu wszelkiego rodzaju przestrzeni. Oto kilka sytuacji, w których ta wiedza jest nieoceniona:

• ogrodnictwo: znajomość obwodu jest kluczowa, gdy trzeba określić długość ogrodzenia dla prostokątnego ogródka,
• budownictwo: w kontekście aranżacji wnętrz, wiedza na temat obwodu prostokąta ma duże znaczenie, np. podczas montażu listew przypodłogowych czy aranżacji opraw oświetleniowych,
• urządzanie wnętrz: dzięki obliczeniu obwodu prostokąta łatwiej jest zaplanować rozmieszczenie mebli oraz ogólną organizację pomieszczenia, co znacząco wpływa na komfort jego użytkowania,
• architektura: w trakcie projektowania budynków, szczególnie tych o prostokątnym kształcie, znajomość obwodu jest istotna dla harmonijnego rozmieszczenia elementów strukturalnych oraz osiągnięcia odpowiedniej estetyki.

Umiejętność obliczania obwodu prostokąta jest zatem nieoceniona w precyzyjnym planowaniu. To kluczowy element w każdej dziedzinie, gdzie przestrzeń odgrywa decydującą rolę.

Jak obwód prostokąta pomaga w mierzeniu ogrodzeń i pomieszczeń?

Obwód prostokąta odgrywa niezwykle ważną rolę, zwłaszcza podczas pomiaru ogrodzeń i przestrzeni. Dzięki prostemu wzorowi, wiedząc, jak długie są boki, bez trudu obliczymy łączną długość ogrodzenia potrzebnego do zabezpieczenia terenu. Na przykład, kiedy planujemy ogrodzenie prostokątnej działki, znajomość obwodu umożliwi nam dokładne określenie ilości materiałów, takich jak słupki czy siatka, które będą niezbędne do prawidłowej instalacji.

Obwód prostokąta ma także swoje zastosowanie w organizacji przestrzeni użytkowej. Mierząc ogrodzenia, można starannie zaplanować:

• układ wnętrza,
• rozmieszczenie mebli,
• efektywne wykorzystanie dostępnego miejsca.

Rzeczywiście, precyzyjne pomiary obwodu przyczyniają się do uzyskania lepszych rezultatów w budownictwie i architekturze.

Zrozumienie znaczenia obwodu prostokąta jest niezwykle pomocne w planowaniu projektów budowlanych oraz w zakupach materiałów. Dzięki temu działamy sprawnie i skutecznie, realizując różnorodne przedsięwzięcia.

Kiedy potrzebne są precyzyjne pomiary obwodu?

Dokładne pomiary obwodu prostokąta odgrywają istotną rolę w wielu dziedzinach, gdzie precyzja jest na wagę złota. Na przykład w architekturze nawet najmniejsza nieścisłość może prowadzić do znaczących kosztów, a w produkcji mebli odpowiednie wymiary są kluczowe dla prawidłowego zestawienia różnych elementów.

W ogrodnictwie znajomość obwodu działki umożliwia skuteczne planowanie rozmieszczenia roślin. Dzięki temu zarówno ich wzrost, jak i ogólny wygląd ogrodu mogą być zoptymalizowane. Dodatkowo, przy układaniu podłóg, precyzyjne pomiary obwodu są istotne dla określenia ilości potrzebnych materiałów.

Aby uzyskać precyzyjne wyniki, wykorzystuje się różnorodne narzędzia, takie jak:

• taśmy miernicze,
• suwmiarki,
• lasery.

Dzięki nim znacząco minimizuje się ryzyko błędów, co jest niezbędne, gdy każdy centymetr ma ogromne znaczenie.

Jak wykorzystać przekątną i twierdzenie Pitagorasa w obliczeniach prostokąta?

Aby skutecznie wykorzystać przekątną i twierdzenie Pitagorasa w obliczeniach prostokąta, warto na początku zrozumieć, czym dokładnie jest przekątna. To linia łącząca przeciwległe wierzchołki prostokąta. Można obliczyć jej długość, stosując wzór: d = √(a² + b²), gdzie „a” i „b” oznaczają długości boków prostokąta.

Twierdzenie Pitagorasa odgrywa kluczową rolę w geometrii, ponieważ umożliwia określenie długości przekątnej, co jest niezwykle przydatne w różnych pomiarach oraz projektach. Na przykład, jeśli chcemy sprawdzić, czy dany obiekt jest prostokątny, wystarczy zmierzyć długości jego boków, a następnie skorzystać ze wspomnianego wzoru, aby znaleźć długość przekątnej. Porównując wyniki pomiarów z obliczeniami, możemy potwierdzić, czy figura rzeczywiście ma kształt prostokąta.

Zrozumienie przekątnej prostokąta wzbogaca naszą wiedzę o wymiarach i ułatwia precyzyjne pomiary oraz obliczenia. Jest to szczególnie istotne zarówno w matematyce, jak i w codziennym życiu, gdzie znajomość twierdzenia Pitagorasa pozwala na lepsze zrozumienie geometrii prostokątów oraz ich praktycznych zastosowań.

Ćwiczenia i zadania interaktywne z obliczania obwodu prostokąta

Ćwiczenia oraz interaktywne zadania dotyczące obliczania obwodu prostokąta stanowią doskonały sposób na rozwijanie umiejętności w zakresie matematyki. Temat obliczania obwodu prostokąta odgrywa kluczową rolę w nauczaniu matematyki, a uczniowie mogą go zgłębiać na wiele różnych sposobów. Oferowane materiały edukacyjne zawierają aż 27 zadań, w tym 16 interaktywnych, które angażują uczniów i umożliwiają praktyczne wykorzystanie zdobytej wiedzy.

Interaktywne zadania pomagają w przyswojeniu wzoru na obwód: O = 2(a + b). Dzięki wizualizacji oraz samodzielnym obliczeniom uczniowie mają szansę lepiej zrozumieć ten materiał. Umożliwia im to określenie długości boków prostokąta na podstawie podanego obwodu, co sprzyja rozwijaniu ich zdolności analitycznych. Dodatkowo, ćwiczenia te są niezwykle pomocne w rysowaniu prostokątów o określonym obwodzie, co jest przydatne w codziennych sytuacjach, takich jak:

• planowanie przestrzeni,
• budowa ogrodzeń,
• tworzenie planów architektonicznych.

W ramach tych materiałów dydaktycznych uczniowie mogą korzystać z różnorodnych przykładów obliczeniowych, co znacząco wzbogaca ich wiedzę. Powtarzalność oraz różnorodność zadań sprawiają, że przyswajanie tematu staje się łatwiejsze. Dzięki temu, uczniowie lepiej przygotowują się na bardziej skomplikowane zagadnienia matematyczne. Warto również zauważyć, że wraz z rozwojem aplikacji oraz platform online, ćwiczenia te stają się o wiele bardziej dostępne, co z kolei zachęca uczniów do aktywnego uczestnictwa w procesie nauki.

Czym różni się obwód prostokąta od pola tej figury?

Obwód prostokąta to całkowita długość wszystkich boków tego kształtu. Aby go obliczyć, można skorzystać z prostego wzoru: O = 2(a + b). Z drugiej strony, pole prostokąta odnosi się do powierzchni wewnętrznej figury i można je wyliczyć, używając innego wzoru: P = a * b.

Kluczowa różnica pomiędzy obwodem a polem polega na tym, że:

• obwód mierzy długość granic prostokąta,
• pole obrazuje, ile obszaru zajmuje dany kształt.

Znajomość obwodu jest pomocna na przykład przy planowaniu materiałów potrzebnych do ogrodzenia, podczas gdy informacja o polu jest istotna przy ocenie powierzchni działki lub podłogi.

Zrozumienie tych różnic jest istotne nie tylko w matematyce, ale także w codziennym życiu. Dzięki nim możemy lepiej planować przestrzeń czy wprowadzać obliczenia finansowe związane z nieruchomościami. Regularne ćwiczenia związane z obliczaniem obwodu i pola prostokąta wspierają rozwój umiejętności geometrycznych, co może przyczynić się do lepszego opanowania tego materiału.

Jak narysować prostokąt o danym obwodzie?

Aby narysować prostokąt o określonym obwodzie, najpierw musimy ustalić długości jego boków, oznaczonych jako a i b. Pamiętajmy o istotnym wzorze: O = 2(a + b). Możemy na przykład zacząć od jednego boku i z tej wartości wyliczyć długość drugiego.

Rozważmy obwód równy 20. Jeśli zdecydujemy się na długość boku a = 4, obliczenie boku b możemy przeprowadzić w kilku prostych krokach:

1. O = 2(a + b) => 20 = 2(4 + b)
2. 20 = 8 + 2b
3. 12 = 2b
4. b = 6.

Gdy już znamy długości boków, mamy możliwość skorzystania z różnorodnych narzędzi, takich jak programy do grafiki komputerowej, które pomogą nam zobrazować prostokąt. Wizualizacje w formie rysunków czy ilustracji znacznie ułatwiają dostrzeżenie relacji między obwodem a długościami poszczególnych boków.

Nie zapominajmy, że dokładność jest kluczowa w tym procesie. Warto sięgnąć po przyrządy jak linijki, komputery czy aplikacje mobilne, które pozwolą nam precyzyjnie odwzorować wymiary prostokąta.

Kiedy znajomość wzoru na obwód prostokąta jest najczęściej wykorzystywana?

Znajomość wzoru na obwód prostokąta odgrywa niezwykle ważną rolę w wielu branżach, w których precyzyjne pomiary są na wagę złota. Oto przykłady zastosowania tego wzoru:

• w architekturze i budownictwie, szybka kalkulacja obwodu umożliwia efektywne planowanie przestrzeni oraz optymalne wykorzystanie materiałów budowlanych,
• w ogrodnictwie, potrzebna jest do wyliczania długości ogrodzeń, co ułatwia oszacowanie kosztów i ilości potrzebnych surowców,
• w projektowaniu wnętrz, wiedza na temat obwodu prostokąta jest kluczowa przy rozmieszczeniu mebli i dodatków w różnych pomieszczeniach,
• w edukacji matematycznej, uczniowie uczą się go na lekcjach geometrii i wykorzystują w praktycznych zadaniach,
• umiejętność ta stanowi podstawę dla bardziej złożonych zagadnień geometrycznych i matematycznych, otwierając drzwi do nowoczesnych wyzwań.

Wzór na obwód prostokąta jest więc nie tylko teorią, ale praktycznym narzędziem, które rozwija zdolności analityczne uczniów i profesjonalistów w różnych branżach.