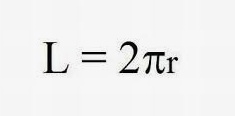Co to jest obwód koła?
Obwód koła to długość linii, która tworzy jego granice. Jest to zamknięta krzywa, składająca się z punktów usytuowanych w równej odległości od centrum koła. W kontekście matematyki oraz geometrii, obwód, oznaczany literą O, stanowi fundamentalne pojęcie, które umożliwia opisanie kształtu oraz rozmiaru okręgu.
Aby ustalić długość obwodu, korzystamy z liczby π (pi), która ilustruje związek między obwodem a średnicą okręgu. To oznacza, że bez względu na wielkość, wszystkie koła dzielą tę samą proporcję. Obliczanie obwodu jest niezwykle istotne, zarówno w zadaniach geometrycznych, jak i w inżynierii, gdzie dokładne pomiary długości okręgów są kluczowe.
Ponadto, obwód koła ma szerokie zastosowanie w wielu dziedzinach, na przykład w:
- projektowaniu mechanicznych komponentów,
- analizie przestrzeni w architekturze,
- rozwiązywaniu problemów związanych z obliczeniami geometrycznymi.
Ta wiedza jest szczególnie wartościowa dla uczniów i studentów zgłębiających tajniki geometrii i matematyki, ponieważ pozwala im lepiej rozumieć i rozwiązywać praktyczne problemy związane z obliczeniami geometrycznymi.
Jakie są wzory na obwód koła?
Obliczanie obwodu koła można przeprowadzić na dwa różne sposoby, korzystając z dwóch kluczowych wzorów matematycznych:
- L = 2πr, gdzie L oznacza obwód, a r jest promieniem koła.
- L = πd, gdzie d to średnica koła.
Warto zwrócić uwagę na następujące aspekty:
- obwód to podwójna wartość liczby π pomnożona przez promień,
- przykład: dla koła z promieniem 5 cm obliczamy: L = 2 × π × 5 cm, co przekłada się na około 31,42 cm,
- średnica (d) jest dwukrotnością promienia (d = 2r),
- w przypadku koła o średnicy 10 cm, obliczenia będą wyglądać następująco: L = π × 10 cm, co również daje około 31,42 cm,
- liczba π (Pi) odgrywa kluczową rolę w tych obliczeniach, reprezentując stosunek obwodu do średnicy koła.
Te wzory umożliwiają łatwe wyliczanie obwodu koła, co może być przydatne zarówno w matematycznych zadaniach, jak i w praktycznych zastosowaniach związanych z geometrią.
Obwód koła przy danym promieniu: O = 2πr
Obliczając obwód koła, posługujemy się prostym wzorem O = 2πr. W nim O to obwód, r reprezentuje promień, a π (pi) ma wartość zbliżoną do 3,14159. Promień koła to odległość, jaka dzieli jego środek od brzegu. Zauważalna zmiana promienia wpływa bezpośrednio na obwód – kiedy promień wzrasta, obwód również rośnie w takim samym stosunku. Dla przykładu, jeśli podniesiemy promień do dwóch razy większej wartości, obliczony obwód również zwiększy się dwukrotnie.
Zrozumienie tego wzoru odgrywa istotną rolę w geometrii. Jest on wykorzystywany w wielu branżach, takich jak:
- architektura,
- inżynieria,
- matematyka.
Dokładne pomiary obwodu są kluczowe, by unikać pomyłek w obliczeniach.
Przykładowo, dla promienia wynoszącego 5 cm, możemy obliczyć obwód w następujący sposób: O = 2 × π × 5 cm, co daje nam wartość około 31,42 cm. Dzięki temu wzorowi z łatwością określimy długość okręgu dla rozmaitych promieni.
Obwód koła przy danej średnicy: O = πd
Obliczenie obwodu koła jest proste dzięki wzorowi O = πd. W tym równaniu O oznacza obwód, d to średnica, a π, znane jako liczba Pi, wynosi około 3,14. W praktyce, wystarczy pomnożyć średnicę przez π, aby uzyskać wartość obwodu.
Wzór ten doskonale ukazuje, że obwód jest bezpośrednio związany ze średnicą. Gdy powiększamy średnicę, obwód również rośnie proporcjonalnie. Na przykład:
- jeśli średnica wynosi 10 cm,
- obliczymy obwód jako O = π × 10 cm,
- co daje nam w przybliżeniu 31,4 cm.
Metoda obliczania obwodu w ten sposób jest nie tylko szybka, ale również skuteczna, zwłaszcza w kontekście geometrii oraz różnorodnych zastosowań praktycznych. Dodatkowo, warto zauważyć, że liczba Pi to stała matematyczna, co czyni ją niezwykle użytecznym narzędziem w wielu obliczeniach związanych z kołami.
Jak działa liczba pi (π) w obwodzie koła?
Liczba pi (π) odgrywa kluczową rolę w obliczeniach związanych z obwodem koła. Jej wartość wynosi około 3,14159 i stanowi stosunek długości obwodu do średnicy. To oznacza, że niezależnie od wielkości koła, jego obwód jest zawsze niemal 3,14 razy większy niż średnica.
Do podstawowych wzorów służących do wyliczania obwodu należą:
- O = 2πr (gdzie r oznacza promień),
- O = πd (gdzie d to średnica).
Pierwszy z nich ilustruje sposób obliczenia obwodu poprzez pomnożenie promienia przez 2 i następnie przez π. Z kolei drugi wzór pokazuje, jak istotna jest średnica w tych obliczeniach.
Pi jest niezwykle pomocne w precyzyjnym przeliczaniu wymiarów koła, co czyni je uniwersalnym narzędziem w matematyce i geometrii. W różnych dziedzinach, od teorii po praktyczne zastosowania w inżynierii, liczba pi pozostaje nieodłącznym elementem wszelkich analiz dotyczących obwodu koła.
Jak obliczyć obwód koła — krok po kroku?
Aby obliczyć obwód koła, musisz znać przynajmniej jego promień lub średnicę. W tym celu wykorzystuje się znane wzory matematyczne.
Jeżeli masz promień koła oznaczony jako r, obliczenia obwodu O wykonasz za pomocą wzoru O = 2·π·r. Dla przykładu, przy promieniu 5 cm, obliczysz obwód jako O = 2·π·5 cm, co daje wynik około 31,4 cm.
Z kolei, jeśli dysponujesz średnicą d, możesz skorzystać z prostszego wzoru O = π·d. Dla średnicy 10 cm otrzymasz O ≈ 31,4 cm.
Nie zapomnij o konieczności dostosowania jednostek, jeżeli zajdzie taka potrzeba. Na przykład, przeliczając centymetry na metry, pamiętaj, że 100 cm odpowiada 1 m.
Jeśli chcesz, możesz również skorzystać z dostępnych online kalkulatorów obwodu koła. To szybka i wygodna metoda, ponieważ wystarczy wpisać promień lub średnicę. Kluczowe jest, by w całym procesie obliczeń stosować te same jednostki miary.
Jak znaleźć promień lub średnicę znając obwód koła?
Aby obliczyć promień lub średnicę koła, posiadając jego obwód O, możemy skorzystać z kilku prostych równań matematycznych. Obwód koła można zdefiniować na dwa różne sposoby:
- pierwszym jest równanie O = 2πr, gdzie r to promień,
- drugim natomiast jest O = πd, gdzie d oznacza średnicę.
Jeśli znamy wartość obwodu, łatwo możemy wyznaczyć promień, dzieląc obwód przez 2π. Oto jak wygląda wzór na promień:
r = O / (2π)
Jeśli chcemy znaleźć średnicę, wystarczy podzielić obwód przez π. Wzór na średnicę przedstawia się następująco:
d = O / π
Na przykład, gdy obwód koła wynosi 31,4 cm, obliczamy promień w następujący sposób:
r = 31,4 / (2 * π) ≈ 5 cm
Tymczasem, aby obliczyć średnicę, wykonujemy następujące działanie:
d = 31,4 / π ≈ 10 cm
Znajomość tych równań znacznie upraszcza prace w geometrii. Co więcej, takie umiejętności są niezwykle przydatne w dziedzinach takich jak budownictwo czy pomiar.
Jaką rolę odgrywa proporcjonalność w obwodzie koła?
Proporcjonalność odgrywa kluczową rolę w zrozumieniu relacji między obwodem koła, jego promieniem a średnicą. Możemy to ująć w postaci zgrabnych wzorów matematycznych:
- O = 2·π·r,
- O = π·d.
W obu przypadkach obwód wzrasta proporcjonalnie do promienia lub średnicy koła.
Na przykład, jeśli zwiększymy promień koła dwukrotnie, obwód także stanie się dwukrotnie większy. Taka zasada jest fundamentem geometrii, ponieważ upraszcza proces skalowania wymiarów koła oraz umożliwia rozwiązanie bardziej skomplikowanych zagadnień matematycznych.
Praktyczne zastosowania proporcjonalności można dostrzec w projektowaniu okrągłych obiektów czy w obliczeniach inżynierskich.
Zrozumienie wzorów dotyczących obwodu oraz koncepcji proporcjonalności ułatwia szybkie przeliczanie różnych parametrów koła. Można je dostosować do konkretnych potrzeb lub obliczeń, co jest niezwykle cenne w naukach ścisłych, gdzie dokładność ma ogromne znaczenie. Proporcjonalność obwodu ma więc wpływ na wiele praktycznych i teoretycznych aspektów w matematyce.
Jakie są jednostki miary obwodu koła i jak je konwertować?
Obwód koła można wyrażać w różnych jednostkach długości, takich jak milimetry (mm), centymetry (cm), metry (m), cale (in), stopy (ft) oraz jardy (yd). Wybór konkretnej jednostki często zależy od zastosowanego systemu miar, czyli metrycznego bądź imperialnego.
Aby przeliczyć różne jednostki, używa się współczynników konwersji. Na przykład, jeden cal równy jest 2,54 centymetra. Z tego powodu, przy przeliczaniu cali na centymetry wystarczy pomnożyć długość w calach przez 2,54. Wiele standardowych przeliczników można znaleźć w literaturze lub skorzystać z narzędzi dostępnych online.
Przykłady przeliczeń mogą wyglądać następująco:
- dziesięć cali to 25,4 centymetra (10 x 2,54 cm),
- jeden metr to 100 centymetrów (1 m = 100 cm),
- pięć jardów można przeliczyć na metry, co daje 4,572 m (5 x 0,9144 m).
Zrozumienie jednostek miary i umiejętność ich konwertowania odgrywa istotną rolę przy obliczaniu obwodu koła. Jest to szczególnie ważne w dziedzinach takich jak inżynieria, budownictwo czy precyzyjne pomiary. Dokładność w obliczeniach wymaga także konsekwencji w używaniu jednostek długości, co w efekcie prowadzi do uzyskania wiarygodnych rezultatów.
Jakie są różnice między obwodem, polem, łukiem i wycinkiem koła?
Obwód, pole, łuk i wycinek koła to kluczowe pojęcia w geometrii, które pełnią istotne funkcje i mają różnorodne zastosowania.
Obwód koła to długość linii otaczającej okrąg. Możemy go łatwo obliczyć, korzystając z formuły O = 2πr, co oznacza, że mówimy tu o sumie wszystkich punktów na granicy koła. Z kolei pole koła odnosi się do powierzchni, którą ono zajmuje, i można je wyznaczyć za pomocą wzoru P = π·r².
Łuk jest częścią okręgu, wyznaczaną przez dwa punkty na obwodzie. Jego długość wyliczamy, uwzględniając miarę kąta środkowego. Natomiast wycinek koła to figura ograniczona łukiem oraz dwoma promieniami, której pole również można obliczyć, biorąc pod uwagę kąt środkowy. Niezwykle istotne jest także zrozumienie, że odcinek koła to część koła ograniczona cięciwą oraz odpowiadającym jej łukiem. W przeciwieństwie do wycinka, odcinek nie zależy od kątów, lecz od segmentu łączącego dwa punkty na obwodzie.
Te różnorodne elementy stanowią fundament geometrii. Ich zgłębienie jest kluczowe dla rozwiązywania problemów związanych z figurami kołowymi oraz przeprowadzania skomplikowanych obliczeń geometrycznych.
Jak precyzyjnie mierzyć długość obwodu koła?
Aby zebrać dokładne dane dotyczące obwodu koła, należy sięgnąć po odpowiednie narzędzia oraz techniki. Pierwszym etapem jest dokonanie wyboru idealnego przyrządu pomiarowego. Zwykle wykorzystywane są:
- taśmy miernicze,
- cyrkle,
- różnego typu urządzenia specjalistyczne.
Te narzędzia mogą dostarczyć zadowalające rezultaty.
Ponadto, obwód koła można obliczyć, korzystając z formuł związanych z promieniem (r) lub średnicą (d) oraz π. Na przykład, obliczenia wykonujemy ze wzoru:
- O = 2πr,
- O = πd.
Te matematyczne wyliczenia generują bardzo precyzyjne wyniki, które znajdują zastosowanie w inżynierii.
Nie bez znaczenia jest używanie odpowiednich jednostek, takich jak metry czy centymetry. Zmiana jednostek, np. przeliczenie cali na centymetry, wpływa na precyzję pomiarów. Dzięki nowoczesnym kalkulatorom dostępnym online można szybko przeprowadzać zarówno:
- obliczenia,
- konwersje.
To znacznie zwiększa efektywność pomiarów.
Uzyskanie precyzyjnych danych dotyczących obwodu koła wymaga umiejętnego połączenia matematyki z odpowiednim wyposażeniem pomiarowym. Takie podejście nie tylko zapewnia dokładność, ale także wiarygodność uzyskanych wyników.
Jakie są zadania i przykłady praktycznych obliczeń obwodu koła w matematyce i geometrii?
Zadania związane z obliczaniem obwodu koła odgrywają istotną rolę w matematyce oraz geometrii. Ich zastosowanie wykracza poza teoretyczne rozważania – są niezwykle przydatne w praktyce, na przykład przy określaniu ilości materiału potrzebnego do stworzenia obręczy, kabli lub różnych elementów budowlanych.
Rozważmy kilka przykładów:
- Obliczanie obwodu koła: kiedy musimy znaleźć obwód koła o promieniu 5 cm, korzystamy ze wzoru O = 2πr. Obliczenie wygląda następująco: O = 2 × π × 5 cm, co pozwala nam uzyskać 10π cm, czyli około 31,42 cm.
- Zastosowanie w budownictwie: w tej dziedzinie często zajmujemy się obliczeniami związków z kolumnami oraz okrągłymi fundamentami. Znalezienie długości obwodu jest kluczowe dla precyzyjnego zaplanowania elementów konstrukcyjnych.
- Długość cięciwy: jeśli interesuje nas obliczenie długości cięciwy w kole o konkretnym wymiarze, możemy to zrobić na wiele sposobów – zarówno geometrycznie, jak i algebraicznie.
W historii jednym z pionierów tego zagadnienia był Eratostenes, który opracował metodę pomiaru obwodu Ziemi, analizując kąt cienia w dwóch różnych lokalizacjach. Stosował przy tym proporcje geometryczne związane z okręgami.
Dzięki współczesnym technologiom, takim jak kalkulatory obwodu koła, proces obliczeń stał się znacznie łatwiejszy i szybszy. Użytkownicy mogą teraz w prosty sposób przeprowadzać złożone obliczenia.
Obliczenia obwodu koła mają również głębsze znaczenie teoretyczne. Pojęcia, takie jak łuk czy wycinek koła, są niezwykle istotne w bardziej złożonych zagadnieniach geometrycznych. Warto pamiętać, że obliczenia te stanowią fundamentalny element matematyki oraz narzędzie, które znajduje praktyczne zastosowanie w codziennym życiu.