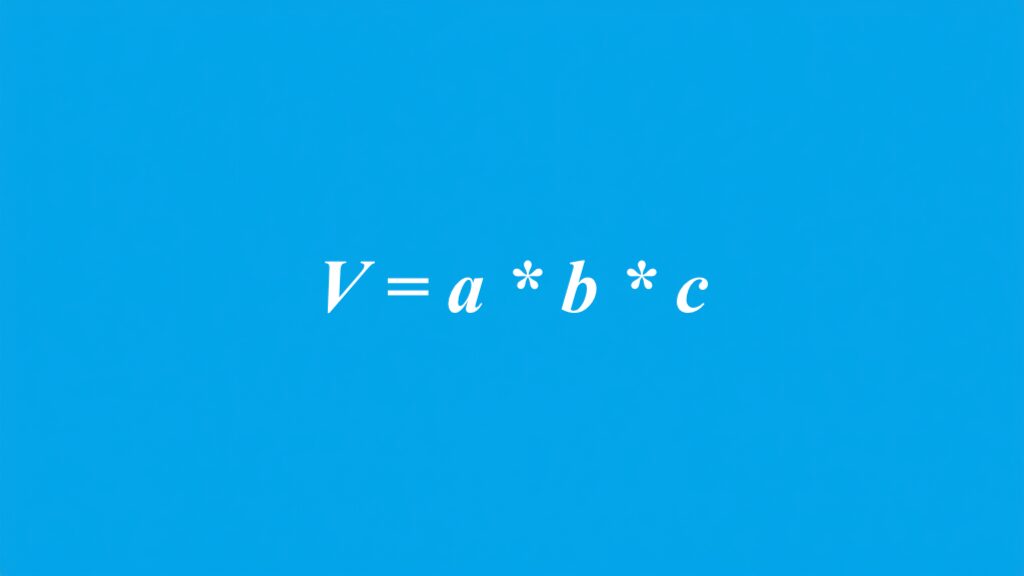Wzór na objętość prostopadłościanu

Prostopadłościan to figura w trzech wymiarach, która składa się z sześciu prostokątnych ścian. Te ściany tworzą trzy pary, które są naprzeciwko siebie. Każda para jest zarówno równoległa, jak i prostopadła do sąsiednich ścian, co sprawia, że prostopadłościan stanowi jeden z najprostszych przykładów graniastosłupa. Jego wymiary obejmują długość, szerokość oraz wysokość.

Ten kształt odgrywa ważną rolę w geometrii przestrzennej. Właściwości prostopadłościanu są niezwykle przydatne w wielu dziedzinach, takich jak:

architektura,
inżynieria,
pakowanie produktów,
planowanie wykorzystania przestrzeni,
analiza materiałów.

Co więcej, prostopadłościan jest kluczowy przy obliczeniach dotyczących objętości oraz pola powierzchni. Dzięki tym obliczeniom uzyskujemy istotne informacje na temat pojemności czy powierzchni materiałów. Jest to nieocenione w praktycznych zastosowaniach. Stosując odpowiednie wzory matematyczne, można szybko i łatwo policzyć te wartości. Dlatego prostopadłościan ma fundamentalne znaczenie w wielu różnych obszarach.

Jak definiowana jest objętość prostopadłościanu?

Objętość prostopadłościanu stanowi jeden z najważniejszych aspektów w geometrii. To miara przestrzeni trójwymiarowej, jaką zajmuje ta figura. Możemy ją obliczyć, mnożąc trzy podstawowe wymiary: długość, szerokość oraz wysokość. Jeśli przyjmiemy, że długość to a, szerokość to b, a wysokość to c, otrzymamy wzór: V = a × b × c.

Wartości te są niezwykle istotne, gdyż pozwalają określić pojemność obiektu, co ma kluczowe znaczenie w takich dziedzinach jak:

projektowanie opakowań,
aranżacja przestrzeni magazynowych.

Dodatkowo oznaczenie objętości literą V sprawia, że łatwiej odróżnić ją od innych wielkości geometrycznych.

Zrozumienie tej definicji jest naprawdę ważne, ponieważ umożliwia swobodne korzystanie z wzoru na objętość prostopadłościanu i rozwiązywanie coraz bardziej złożonych zadań związanych z geometrią.

Jaki jest wzór na objętość prostopadłościanu?

Wzór na objętość prostopadłościanu to V = a * b * c. W tej formule V symbolizuje objętość, natomiast a, b i c odpowiadają kolejno za długość, szerokość oraz wysokość danego obiektu. Aby obliczyć objętość, wystarczy pomnożyć te trzy wymiary. To szybki i skuteczny sposób na uzyskanie rezultatu. Na przykład, gdy a wynosi 5 cm, b 3 cm, a c 4 cm, obliczamy objętość prostopadłościanu jako 5 * 3 * 4, co daje nam wynik 60 cm³.

Sześcian, który jest szczególnym rodzajem prostopadłościanu, charakteryzuje się tym, że wszystkie jego krawędzie są równe. W jego przypadku wzór na objętość ulega uproszczeniu i przyjmuje formę a³. Oznacza to, że do obliczeń wykorzystujemy potęgowanie długości krawędzi.

Wzór V = a * b * c odgrywa kluczową rolę w wielu branżach, takich jak:

architektura,
inżynieria,
codzienne życie.

Często zachodzi potrzeba określenia objętości różnych pojemników, budynków czy przestrzeni użytkowej. Dlatego znajomość tego wzoru jest naprawdę niezwykle przydatna.

Jakie wymiary są potrzebne do obliczenia objętości prostopadłościanu?

Aby obliczyć objętość prostopadłościanu, potrzebujemy trzech podstawowych wymiarów:

długości,
szerokości,
wysokości.

Te wartości odpowiadają krawędziom, które wychodzą z jednego wierzchołka prostopadłościanu. Długość i szerokość tworzą podstawę, a wysokość definiuje, jak wysoko obiekt sięga w górę.

Wszystkie te wymiary powinny być zmierzone lub dostarczone. Kiedy je już mamy, możemy bez trudu obliczyć objętość prostopadłościanu. Cała sztuka polega na pomnożeniu:

długości,
szerokości,
wysokości.

I to wszystko, co potrzebne, by uzyskać wynik!

Co oznacza V we wzorze na objętość prostopadłościanu?

Litera V w kontekście objętości prostopadłościanu symbolizuje przestrzeń, którą dana bryła zajmuje. To powszechnie używany znak w matematyce, który odnosi się do pojemności w różnych dyscyplinach nauki.

Wzór na obliczenie objętości prostopadłościanu przedstawia się jako V = a * b * c, gdzie:

a to długość,
b to szerokość,
c to wysokość tej bryły.

Dzięki temu równaniu możemy w prosty sposób określić, ile miejsca zajmuje prostopadłościan. Takie obliczenia są niezwykle istotne w wielu dziedzinach, takich jak:

architektura,
inżynieria,
projektowanie wnętrz,
budownictwo,
logistyka.

Jak obliczyć objętość prostopadłościanu krok po kroku?

Aby obliczyć objętość prostopadłościanu, wystarczy postępować według kilku łatwych kroków. Zacznij od zmierzenia długości, szerokości oraz wysokości tego kształtu – te trzy wymiary będą niezbędne do dalszych obliczeń.

Kolejnym etapem jest skorzystanie z formuły na objętość:

V = a * b * c, gdzie:

a oznacza długość,
b to szerokość,
c to wysokość.

Teraz po prostu pomnóż te trzy wartości, aby uzyskać objętość. Nie zapomnij podać wyniku w odpowiednich jednostkach, takich jak centymetry sześcienne (cm³), decymetry sześcienne (dm³) lub metry sześcienne (m³).

Warto pamiętać, że precyzyjność pomiarów ma ogromne znaczenie. Dzięki dokładnym wartościom bez trudu ustalisz pojemność prostopadłościanu. To może okazać się przydatne w wielu sytuacjach, na przykład w projektowaniu mebli lub przy obliczaniu pojemności różnego rodzaju zbiorników.

Jak stosować jednostki sześcienne w zadaniach?

Jednostki sześcienne są niezwykle istotne, gdy chodzi o obliczanie objętości obiektów geometrycznych, a zwłaszcza prostopadłościanów. Posługując się jednostkami takimi jak centymetry sześcienne (cm³), decymetry sześcienne (dm³) czy metry sześcienne (m³), można precyzyjnie oszacować przestrzeń zajmowaną przez różne przedmioty.

Aby prawidłowo wykorzystać jednostki sześcienne w zadaniach, istotne jest, aby wszystkie wymiary prostopadłościanu — długość, szerokość oraz wysokość — były wyrażone w tych samych jednostkach. Gdy na przykład długość jest podana w centymetrach, to również szerokość i wysokość należy wyrazić w centymetrach. Następnie, mnożąc te wartości:

długość × szerokość × wysokość,

uzyskujemy wynik w jednostkach sześciennych.

Warto mieć na uwadze, że po zakończonych obliczeniach, wynik powinien być zapisany w odpowiednich jednostkach sześciennych, które odpowiadają wcześniej zastosowanym jednostkom liniowym. Tak więc, jeśli wszystkie wymiary to centymetry, objętość zostanie podana jako centymetry sześcienne (cm³). Dzięki temu wyniki stają się bardziej zrozumiałe i łatwiejsze do zastosowania w codziennej praktyce.

Jak przekształcać wzór na objętość w zależności od brakującego wymiaru?

Przekształcanie wzoru na objętość prostopadłościanu, który można zapisać jako V = a * b * c, pozwala na odnalezienie brakującego wymiaru, gdy dysponujemy pozostałymi wartościami. Kiedy znamy objętość oraz dwa z trzech wymiarów (a, b, c), łatwo wyliczamy ten brakujący. Na przykład, aby obliczyć wysokość h, wystarczy zastosować wzór h = V / (a * b).

Jeśli brakuje nam szerokości lub długości, sięgamy po odpowiednie formuły:

a = V / (b * c) dla długości,
b = V / (a * c) dla szerokości.

Dzięki tym metamorfozom wzorów możemy skutecznie rozwiązywać różnorodne zadania geometryczne, nawet w przypadku brakujących danych. Te obliczenia mają znaczenie nie tylko w teorii, ale także w praktycznych zastosowaniach, jak projektowanie przestrzeni czy określanie pojemności.

Warto mieć na uwadze, że przekształcanie wzoru wymaga umiejętności związanych z mnożeniem i dzieleniem, co sprawia, że tematyka ta jest dostępna dla uczniów na różnych etapach edukacji.

Jakie są jednostki objętości i kiedy je stosować?

Jednostki objętości mają kluczowe znaczenie w matematyce i naukach ścisłych. Wyróżniamy trzy najczęściej stosowane:

centymetry sześcienne (cm³),
decymetry sześcienne (dm³),
metry sześcienne (m³).

Centymetry sześcienne (cm³) idealnie nadają się do pomiaru drobnych przedmiotów. Często wykorzystywane są w laboratoriach do określenia objętości małych pojemników czy substancji chemicznych. Na przykład, kontener o pojemności 100 cm³ sprawdzi się doskonale w przechowywaniu niewielkich ilości płynów czy proszków.

Decymetry sześcienne (dm³) są bardziej odpowiednie do mierzenia obiektów średniej wielkości, takich jak butelki, słoiki czy większe naczynia. Jeden decymetr sześcienny to aż 1000 cm³, co czyni go praktycznym wyborem dla przedmiotów, które nie wymagają stosowania metrów sześciennych.

Metry sześcienne (m³) są stosowane do określania dużych przestrzeni, takich jak pomieszczenia, zbiorniki wodne czy całe obszary budowlane. Jeden metr sześcienny odpowiada 1,000,000 cm³ lub 1000 dm³. Ta jednostka jest szczególnie użyteczna w budownictwie oraz architekturze, gdzie precyzyjne pomiary są kluczowe.

Wybór odpowiedniej jednostki objętości zależy przede wszystkim od rozmiaru analizowanych obiektów oraz kontekstu, w jakim są one badane. Istotne jest, aby przy podjęciu decyzji o konkretnej jednostce uwzględnić skalę danego obiektu, co pozwala na zwiększenie precyzji pomiarów.

Czym różnią się centymetry sześcienne (cm³), decymetry sześcienne (dm³) i metry sześcienne (m³)?

Centymetry sześcienne (cm³), decymetry sześcienne (dm³) oraz metry sześcienne (m³) to jednostki objętości, które znajdują zastosowanie w różnych kontekstach. Centymetr sześcienny odnosi się do objętości sześcianu o krawędzi wynoszącej 1 centymetr, co czyni go idealnym narzędziem do pomiarów niewielkich obiektów. Z kolei decymetr sześcienny, który mierzy objętość sześcianu o krawędzi 10 centymetrów, sprawdza się doskonale w przypadku większych przedmiotów, takich jak pojemniki czy mniejsze meble. Natomiast metr sześcienny, definiowany jako objętość sześcianu o krawędzi 1 metra, jest zalecany przy pomiarach znacznie większych obiektów, na przykład budynków lub zbiorników na wodę.

Przy użyciu prostych obliczeń możemy lepiej zrozumieć relacje między tymi jednostkami:

jeden decymetr sześcienny to równowartość tysiąca centymetrów sześciennych,
jeden metr sześcienny odpowiada tysiącu decymetrów sześciennych.

Wiedza o tym, jakie jednostki stosować, jest niezwykle ważna w praktycznych sytuacjach, takich jak:

obliczenia inżynieryjne,
projektowanie architektoniczne,
codzienne pomiary w różnych dziedzinach życia.

Jak obliczyć objętość sześcianu jako szczególnego przypadku prostopadłościanu?

Sześcian to szczególny rodzaj prostopadłościanu, charakteryzujący się tym, że wszystkie jego krawędzie są jednakowej długości, oznaczanej symbolem a. Obliczanie jego objętości jest niezwykle proste i opiera się na krótkim wzorze: V = a³.

Aby obliczyć objętość sześcianu, wystarczy podnieść długość krawędzi do potęgi trzeciej. Na przykład, mając krawędź o długości 2 cm, obliczamy objętość, używając wzoru: V = 2³, co daje nam wynik 8 cm³.

Znajomość objętości sześcianu jest przydatna w wielu dziedzinach, takich jak:

architektura,
projektowanie przestrzeni,
produkcja opakowań,
matematyka,
przemysł.

Sześciany otaczają nas na co dzień – spotykamy je w postaci pojemników czy opakowań. Dlatego umiejętność ich obliczania staje się nie tylko praktyczna, ale i niezwykle użyteczna w codziennym życiu.

Kiedy objętość prostopadłościanu jest równa iloczynowi pola podstawy i wysokości?

Objętość prostopadłościanu można obliczyć, mnożąc pole jego podstawy przez wysokość. Taki sposób wynika z definicji matematycznej objętości tego kształtu.

Aby wyliczyć pole podstawy prostopadłościanu, wystarczy pomnożyć długość przez szerokość. Dlatego wzór na objętość przyjmuje formę:

V = P_podstawy × h

Gdzie:

V oznacza objętość,
P_podstawy to pole podstawy,
h to wysokość obiektu.

Jeśli znasz wartości pola podstawy i wysokości, bez trudu obliczysz objętość prostopadłościanu. To jedna z fundamentalnych reguł w geometrii przestrzennej.

Jak praktycznie zastosować wzór na objętość prostopadłościanu? (Przykłady)

Zastosowanie wzoru na objętość prostopadłościanu odgrywa kluczową rolę w wielu codziennych sytuacjach, zwłaszcza przy obliczaniu pojemności różnych przedmiotów. Prostopadłościany są powszechnie spotykane w naszym otoczeniu, a umiejętność ich obliczania okazuje się niezwykle przydatna w praktyce.

Na przykład, gdy mamy akwarium w kształcie prostopadłościanu, możemy łatwo określić, ile litrów wody jest w środku. Dla akwarium o wymiarach 60 cm długości, 30 cm szerokości i 40 cm wysokości, wystarczy zastosować wzór V = a × b × h. W naszym przypadku będzie to 60 × 30 × 40, co daje imponujące 72 000 cm³, czyli równowartość 72 litrów.

Podobnie możemy obliczać objętość basenów. Na przykład, basen o długości 8 m, szerokości 4 m i głębokości 1,5 m ma objętość wynoszącą 8 × 4 × 1,5, co daje nam 48 m³, a to odpowiada aż 48 000 litrów. Znajomość tej metody obliczeń ułatwia również planowanie przestrzeni do przechowywania – zarówno w szafach, jak i w pudełkach używanych do transportu różnych artykułów.

Warto dodać, że wzór na obliczanie objętości prostopadłościanów znajduje zastosowanie także w projektowaniu mebli czy pakowaniu produktów. Dokładne obliczenia zapewniają optymalne wykorzystanie dostępnej przestrzeni. Zatem, umiejętność obliczania objętości prostopadłościanu ma nie tylko swoje teoretyczne podstawy, ale przede wszystkim realne, praktyczne znaczenie w naszym codziennym życiu.

Jak obliczyć pojemność prostopadłościanu w życiu codziennym?

Aby określić pojemność prostopadłościanu, musimy najpierw zmierzyć jego wymiary: długość, szerokość i wysokość. Używamy do tego prostego wzoru: V = a * b * c, gdzie „a” to długość, „b” to szerokość, a „c” to wysokość. Na przykład, mając pudełko o wymiarach 2 dm (długość) x 3 dm (szerokość) x 4 dm (wysokość), wykonujemy obliczenia: 2 * 3 * 4, co daje nam 24 dm³.

Wynik, wyrażony w jednostkach sześciennych, informuje nas o tym, ile substancji, na przykład wody czy piasku, można pomieścić w danym pojemniku. Jest to niezwykle użyteczna umiejętność w praktyce, na przykład:

w akwarystyce, znajomość pojemności akwarium jest kluczowa, aby dowiedzieć się, ile ryb można w nim hodować,
przy projektowaniu basenów, ważne jest obliczenie ich pojemności, szczególnie w kontekście napełniania ich wodą.

Z tego powodu umiejętność obliczania pojemności prostopadłościanów ma szerokie zastosowanie w wielu aspektach codziennego życia.

Na czym polega różnica między prostopadłościanem a innymi graniastosłupami?

Prostopadłościan to wyjątkowy typ graniastosłupa, którego wszystkie ściany mają formę prostokątów. W odróżnieniu od innych graniastosłupów, jak na przykład te posiadające trójkątne lub wielokątne podstawy, prostopadłościan charakteryzuje się kątami prostymi, gdzie każdy z nich wynosi dokładnie 90 stopni. Dzięki temu, każda para przeciwległych ścian pozostaje równoległa oraz prostopadła do swoich sąsiednich.

Inne graniastosłupy mogą mieć podstawy o różnych kształtach, co dodaje im różnorodności i sprawia, że ich struktura jest bardziej złożona. Przykładowo, graniastosłup trójkątny ma podstawę w formie trójkąta, a jego boczne ściany przypominają równoległoboki, co sprawia, że nie są one prostokątne.

Warto również podkreślić, że chociaż wszystkie prostopadłościany są klasyfikowane jako graniastosłupy, to nie każdy graniastosłup spełnia kryteria prostopadłościanu. Ten szczególny kształt geometryczny cieszy się szerokim zastosowaniem zarówno w geometrii, jak i w praktycznych dziedzinach, takich jak inżynieria czy architektura.

Czy wzór na objętość prostopadłościanu wymaga użycia twierdzenia Pitagorasa lub funkcji trygonometrycznych?

Wzór na objętość prostopadłościanu jest prosty: V = a * b * c. Przy obliczeniach korzystamy z trzech wymiarów – długości (a), szerokości (b) oraz wysokości (c) – co wymaga jedynie podstawowego mnożenia. W tym przypadku nie musimy sięgać po twierdzenie Pitagorasa ani nie potrzebujemy funkcji trygonometrycznych, co czyni proces wyjątkowo przystępnym.

Jednakże w bardziej rozbudowanych sytuacjach, na przykład gdy obliczamy objętość na podstawie przekątnych czy kątów między nimi, twierdzenie Pitagorasa może okazać się nieocenioną pomocą. Jeśli chcemy wyznaczyć długość przekątnej, zastosujemy wzór a² + b² = d², gdzie d reprezentuje długość przekątnej. Z kolei funkcje trygonometryczne, takie jak tangens czy cotangens, mogą pomóc w ustaleniu kątów w bryłach, co również przyczynia się do dokładnego obliczania objętości.

W praktycznych zastosowaniach wystarczy korzystać z podstawowego wzoru na objętość prostopadłościanu. Sprawdza się on doskonale w obliczeniach dotyczących pojemności różnych kontenerów czy przestrzeni w pomieszczeniach. Takie podejście jest wystarczające, aby zaspokoić wiele codziennych potrzeb.