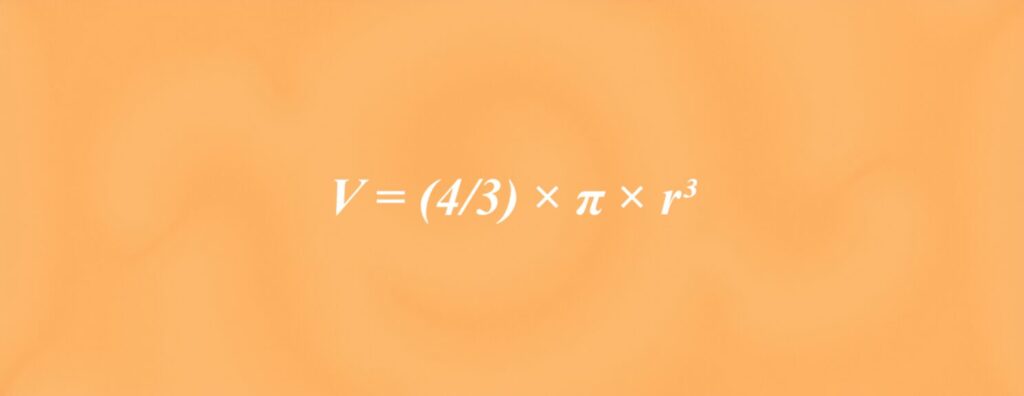Wzór na objętość kuli

Kula w geometrii to trójwymiarowy kształt, który powstaje, gdy koło obraca się wokół swojej średnicy. Jedną z jej najbardziej charakterystycznych cech jest symetria. Powierzchnia kuli składa się z punktów, które znajdują się w równej odległości od środka, określanej jako promień.

Ten geometryczny obiekt odgrywa kluczową rolę w geometrii przestrzennej i ma istotne znaczenie w różnych dziedzinach matematyki oraz inżynierii. W praktyce jego właściwości są nieocenione, na przykład w obliczeniach objętości i pola powierzchni, co podkreśla jego istotność. Obliczając objętość kuli, korzystamy z promienia oraz liczby π (pi), która wynosi około 3,14. Znajomość właściwości kuli ułatwia przeprowadzanie bardziej zaawansowanych obliczeń geometrycznych, a także jest niezbędna w naukach przyrodniczych oraz technologii.

Kula to nie tylko teoretyczna koncepcja matematyczna; ma również praktyczne zastosowania. Jest szeroko wykorzystywana w:

projektowaniu kulistych struktur,
obiektów w architekturze,
sztuce.

To sprawia, że jest niezwykle wszechstronna i użyteczna w różnych kontekstach.

Jak wygląda wzór na objętość kuli?

Wzór na objętość kuli jest kluczowym elementem w geometrii przestrzennej. Ułatwia nam precyzyjne obliczenie przestrzeni zajmowanej przez obiekty o kształcie kulistym. Matematycznie, możemy go przedstawić jako V = (4/3) × π × r³. W tym równaniu V symbolizuje objętość, r to promień kuli, a π (pi) to stała matematyczna, której wartość wynosi około 3,14159.

Jednym z największych atutów tego wzoru jest jego wszechstronność. Umożliwia szybkie oraz dokładne obliczenia; aby określić objętość kuli, wystarczy znać długość promienia. Podnosząc go do trzeciej potęgi, a następnie mnożąc przez π oraz stałą (4/3), otrzymujemy precyzyjny wynik.

Wzór ten ma zastosowanie w wielu dziedzinach, takich jak:

fizyka,
inżynieria,
projektowanie struktur sferycznych.

Pomaga obliczać objętości przedmiotów takich jak piłki, bańki mydlane czy balony. Znalezienie objętości kuli nie tylko wspiera nauki ścisłe, lecz również bywa użyteczne w codziennych sytuacjach, gdzie wiedza o przestrzeni zajmowanej przez różne przedmioty okazuje się niezwykle pomocna.

Jakie są elementy niezbędne do obliczenia objętości kuli?

Aby obliczyć objętość kuli, ważne jest, aby zrozumieć kilka podstawowych pojęć. Dwa istotne elementy to:

promień kuli – odległość mierzona od środka kuli do jej powłok,
liczba π (pi) – stała matematyczna, która przyjmuje wartość w przybliżeniu 3,14.

Wzór na objętość kuli przedstawia się następująco: V = (4/3)πr³, gdzie „r” oznacza promień. Warto również wspomnieć o:

średnicy – która jest dwukrotną wartością promienia (d = 2r),
znalezienie średnicy może znacząco uprościć obliczanie promienia,
co zdecydowanie ułatwia dalsze wyliczenia.

Zarówno promień, jak i liczba π są kluczowe, aby otrzymać precyzyjny wynik przy wyznaczaniu objętości kuli.

Rola promienia i średnicy w obliczeniach

Promień i średnica odgrywają kluczową rolę w obliczeniach związanych z objętością kuli. Promień, który wyznacza wielkość kuli, ma bezpośredni wpływ na jej objętość. Wzór na obliczenie tej objętości to V = (4/3)πr³. W tym równaniu V oznacza objętość, π to stała matematyczna, a r symbolizuje promień.

Średnica, będąca dwukrotnością promienia (d = 2r), również ma znaczenie w tych wyliczeniach. Dzięki temu możemy łatwo przeliczyć średnicę na promień, co pozwala na wykorzystanie tego samego wzoru do ustalenia objętości kuli. Wiedząc, jaka jest średnica, możemy z łatwością określić promień i obliczyć objętość.

W praktycznym zastosowaniu, przy obliczeniach obwodu kuli czy innych parametrów geometrycznych, znajomość promienia i średnicy jest niezbędna. Rozpoznawanie popularnych wzorów oraz umiejętność przeliczania tych dwóch jednostek znacznie ułatwia rozwiązywanie bardziej skomplikowanych problemów geomatrycznych.

Znaczenie liczby π (pi) w wzorze

Liczba π (pi) odgrywa kluczową rolę w obliczeniach związanych z objętością kuli. To liczba nieskończona i niewymierna, wynosząca w przybliżeniu 3,14159. Jej znaczenie w matematyce polega na umożliwieniu precyzyjnego obliczania objętości trójwymiarowych obiektów, takich jak kule. Wzór na objętość kuli można zdefiniować jako V = (4/3)πr³, gdzie V to objętość, a r oznacza promień kuli.

Zastosowanie liczby π w tym równaniu uwzględnia krzywiznę kuli, co jest niezwykle istotne. Wartości objętości kuli różnią się znacznie od objętości prostopadłościanów czy innych brył o prostych krawędziach. Dzięki π możemy uzyskać precyzyjne wyniki, które mają istotne znaczenie w naukach przyrodniczych, inżynierii oraz matematyce. Bez tej fundamentalnej stałej, dokładne określenie miejsca zajmowanego przez kulę byłoby ogromnie trudne.

Zrozumienie liczby π oraz jej różnorodnych zastosowań to niezbędny krok dla każdego, kto pragnie zgłębiać tajniki geometrii.

Jak obliczyć objętość kuli krok po kroku?

Obliczanie objętości kuli to kluczowe zadanie w geometrii. W tym celu posługujemy się wzorem V = (4/3) × π × r³, gdzie r oznacza promień kuli. Cały proces można zredukować do kilku prostych kroków:

zmierz promień kuli, jeśli dysponujesz średnicą, podziel ją przez dwa, aby uzyskać poszukiwany promień,
podnieś tę wartość do trzeciej potęgi (r³), mnożąc promień przez siebie dwa dodatkowe razy: r × r × r,
pomnóż tę wartość przez π (Pi), które wynosi mniej więcej 3,14; jeśli potrzebujesz, sięgnij po dokładniejszą wartość liczby Pi,
na finał, wynik pomnóż przez 4/3; w ten sposób otrzymasz objętość kuli, a jej jednostką będą na przykład centymetry sześcienne (cm³).

Jeśli zaczynasz od średnicy, najpierw oblicz promień dzieląc średnicę przez dwa. A jeśli znasz objętość kuli i chcesz znaleźć promień, możesz skorzystać ze wzoru r = ((3V)/(4π))^(1/3).

Stosując te proste kroki, z łatwością wyliczysz objętość dowolnej kuli. Ta umiejętność jest niezwykle przydatna w wielu dziedzinach, od nauki po inżynierię.

Obliczanie objętości kuli mając promień

Aby obliczyć objętość kuli na podstawie jej promienia, możemy skorzystać z wzoru V = (4/3) × π × r³. W tej formule V oznacza objętość, π to stała matematyczna znana jako liczba Pi, a r to promień kuli.

Oto etapy obliczeń:

podnieś promień do potęgi trzeciej (r³),
pomnóż otrzymaną wartość przez π,
pomnóż wynik przez 4/3.

Dzięki temu prostemu równaniu uzyskujemy precyzyjny wynik, który można obliczyć w mgnieniu oka.

Przykładowo, jeżeli mamy kulę o promieniu 5 cm, obliczenia wyglądają następująco:

najpierw r³ = 5³, co daje 125,
następnie mnożymy 125 przez π, co daje nam w przybliżeniu 392,7,
na koniec, wykonujemy mnożenie (4/3) × 392,7, co prowadzi do wyniku około 523,6 cm³.

Ta metoda obliczania objętości kuli ukazuje, jak kluczowy jest promień w geometrii brył. Jego wartość wpływa na różne cechy kuli, co czyni go bardzo istotnym elementem w wszelkiego rodzaju obliczeniach związanych z objętością.

Obliczanie objętości kuli mając średnicę

Obliczanie objętości kuli zaczyna się od przekształcenia średnicy na promień. Warto pamiętać, że średnica jest dwukrotnością promienia, więc aby uzyskać promień, wystarczy podzielić średnicę przez 2.

Gdy już mamy promień, możemy przejść do obliczenia objętości, korzystając z następującego wzoru: V = (4/3) × π × r³, gdzie r oznacza promień. Jeśli wolisz pracować ze średnicą, dostępny jest również inny wzór: V = (1/6) × π × d³, gdzie d to średnica.

Przykładowo, mając kulę o średnicy 6 cm, promień wyniesie 3 cm (czyli 6 cm podzielone przez 2). Po podstawieniu tej wartości do wzoru, otrzymujemy: V = (4/3) × π × 3³. To przeliczenie daje nam około 113,1 cm³.

Stosując takie metody, można szybko i efektywnie obliczyć objętość kuli. Znajomość odpowiednich wzorów jest niezwykle ważna, szczególnie w geometrii, ponieważ umożliwia uzyskanie dokładnych wyników w krótkim czasie.

Jak wyznaczyć promień kuli znając objętość?

Aby obliczyć promień kuli znając jej objętość, musimy skorzystać z wzoru, który jest odwrotnością standardowego równania dla objętości. Jak wiadomo, objętość kuli wyraża się jako V = (4/3)πr³, gdzie V to objętość, a r oznacza promień. Przekształcając ten wzór, uzyskujemy formułę do wyliczenia promienia:

r = ∛(3V / 4π).

Oto, co należy zrobić, aby ustalić promień kuli:

zmierz objętość kuli (V),
wprowadź tę zmierzoną wartość do wzoru r = ∛(3V / 4π),
przeprowadź obliczenia, aby uzyskać ostateczną wartość promienia (r).

Na przykład, mając kulę o objętości 100 cm³, wstawiając ją do wzoru, możemy obliczyć promień:

r = ∛(3 × 100 / 4π) ≈ 2,15 cm.

Zrozumienie tego wzoru jest cenne nie tylko w kontekście matematycznym, ale także w różnych praktycznych zastosowaniach. Umożliwia on łatwe określenie wymiarów kuli na podstawie jej objętości, co przydaje się w wielu dziedzinach.

Co to jest półkula i jak obliczyć jej objętość?

Półkula to ciekawa figura geometryczna, której objętość można łatwo obliczyć przy pomocy wzoru V = (2/3) × π × r³, gdzie „r” to promień półkuli. Półkula powstaje w wyniku przecięcia kuli z płaszczyzną, która przechodzi przez jej środek. Dzięki tej właściwości znajduje wiele zastosowań w geometrii przestrzennej oraz w praktycznych obliczeniach objętości.

Aby obliczyć objętość półkuli, musimy znać jej promień. Na przykład:

jeżeli promień wynosi 4 cm, obliczenia będą wyglądać następująco: V = (2/3) × π × (4)³, co daje nam V ≈ 33,51 cm³,
jeżeli mamy średnicę półkuli równą 8 cm, łatwo przeliczymy promień, korzystając z wzoru r = d/2, co w tym przypadku daje 4 cm.

Oprócz teorii, półkula ma wiele praktycznych zastosowań w życiu codziennym, takich jak:

misy,
półkuliste pokrywy.

Obliczenia objętości są szczególnie ważne w dziedzinach takich jak inżynieria czy projektowanie, gdzie dokładne wymiary odgrywają kluczową rolę.

Jak wyprowadzić wzór na objętość kuli?

Aby obliczyć objętość kuli, korzystamy z narzędzi analizy matematycznej oraz rachunku całkowego. Proces ten polega na podzieleniu kuli na nieskończoną liczbę cienkich warstw, które następnie zliczamy, aby uzyskać łączną objętość.

Na początku zakładamy, że kula o promieniu r znajduje się w układzie współrzędnych. Tworzymy cienkie warstwy w postaci dysków o promieniu x i grubości dy. Z geometrii wiemy, że objętość takiego dysku wyrażamy za pomocą wzoru:

dV = πx²dy

Aby określić wartość x w odniesieniu do y, posługujemy się wzorem x = √(r² – y²). Po podstawieniu tej relacji do równania objętości, otrzymujemy:

dV = π(r² – y²)dy

Następnie przeprowadzamy całkowanie tej funkcji w granicach od -r do r:

V = ∫_{-r}^{r} π(r² – y²)dy

Po wykonaniu obliczeń, tych związanych z całkami i właściwościami funkcji, dochodzimy do końcowego wyniku:

V = (4/3)πr³

To klasyczne wyprowadzenie wzoru ilustruje, jak można zastosować całki w geometrii. Co więcej, stanowi ono fundament do zrozumienia charakterystyki brył obrotowych.

Zastosowanie analizy matematycznej i rachunku całkowego

Analiza matematyczna oraz rachunek całkowy to fundamentalne narzędzia w zakresie matematyki wyższej, szczególnie podczas obliczania objętości kuli. W tym celu wykorzystujemy sumowanie nieskończono małych elementów objętości, co jest kluczowe dla zgłębiania problematyki brył obrotowych.

Metody całkowe umożliwiają modelowanie objętości kuli, co w efekcie pozwala na uwzględnienie bardziej skomplikowanej geometrii przestrzennej. Wzór na objętość kuli, zapisany jako V = (4/3)πr³ (gdzie r oznacza promień), powstał dzięki zastosowaniu analiz matematycznych. Korzystając z całek, jesteśmy w stanie przeprowadzać obliczenia z dokładnością, co w konsekwencji prowadzi do precyzyjnych wyników objętości. Ta wiedza jest również istotna w dziedzinie inżynierii oraz fizyki.

Analiza matematyczna dostarcza teoretycznych fundamentów, które uczą nas, jak wykorzystać rachunek całkowy w praktycznych zastosowaniach. Dzięki tym technikom potrafimy nie tylko wyprowadzić wzór na objętość kuli, ale również wprowadzić kluczowe pojęcia związane z obliczeniami, które różnią się w zależności od liczby elementów. Takie podejście odgrywa istotną rolę w edukacji matematycznej studentów kierunków inżynieryjnych i nauk ścisłych, ponieważ zrozumienie wpływu teorii na praktykę jest niezbędne w ich dalszej karierze.

Jakie są jednostki objętości – cm³ i inne?

Objętość kuli zazwyczaj wyrażamy w jednostkach sześciennych, z których najpopularniejszym wyborem jest centymetr sześcienny (cm³). Ta jednostka, uznawana w systemie metrycznym, wskazuje nam, ile przestrzeni zajmuje kula. Dla lepszego zobrazowania: kula o objętości 1 cm³ zajmuje miejsce odpowiadające sześcianowi o boku 1 centymetra.

Możemy także przedstawić objętość kuli w metrach sześciennych (m³), co jest szczególnie przydatne w kontekście większych miar, takich jak te stosowane w budownictwie czy inżynierii. W obszarze nauk ścisłych spotykamy także inne jednostki, na przykład litry, które odpowiednio są związane z objętością, ponieważ 1 litr to 1000 cm³.

Te jednostki mają kluczowe znaczenie w wielu dziedzinach, od fizyki po chemię, umożliwiając nam dokładne obliczenia i precyzyjne pomiary. Znajomość jednostek objętości ułatwia zrozumienie procesów związanych z pojemnością różnych zbiorników oraz przepływem cieczy. Warto zatem umieć właściwie interpretować objętość w różnych jednostkach, co jest nie tylko teoretyczną, ale i praktyczną umiejętnością.

Jak można wykorzystać kalkulator objętości kuli?

Kalkulator objętości kuli to niezwykle przydatne narzędzie, które znacznie upraszcza obliczanie objętości tych brył na podstawie promienia lub średnicy. Umożliwia szybkie i precyzyjne wyliczenia, co znacznie minimalizuje ryzyko popełnienia błędów, jakie mogą występować podczas ręcznych obliczeń. Jego wartość szczególnie doceniają uczniowie, inżynierowie oraz specjaliści z różnych dziedzin naukowych.

W ramach edukacji i w laboratoriach inżynieryjnych, kalkulator objętości kuli wspiera zarówno uczniów, jak i profesjonalistów w zrozumieniu oraz zastosowaniu wzoru V = (4/3) × π × r³. Wystarczy tylko wpisać wartość promienia lub średnicy, aby uzyskać wynik w ułamku sekundy. Takie aplikacje internetowe lub mobilne ułatwiają przyswajanie podstawowych koncepcji geometrycznych, co znacznie przyspiesza naukę.

Oprócz obliczeń objętości kuli, to narzędzie pozwala również na przeprowadzanie różnorodnych analiz porównawczych, na przykład zestawiając objętości kul o różnych promieniach. Sprawdza się także w praktycznych zastosowaniach, na przykład przy projektowaniu okrągłych obiektów, jak kuliste zbiorniki czy pomoce dydaktyczne.

Współczesne kalkulatory objętości kuli często posiadają dodatkowe funkcje, takie jak:

przeliczanie jednostek,
analizę porównawczą objętości,
szybkie obliczenia,
wsparcie w nauce matematyki,
zastosowania w inżynierii.

To znacząco rozszerza ich zastosowanie w codziennych zadaniach inżynierów oraz naukowców.

Jak wzór na objętość kuli znajduje zastosowanie w praktyce?

Wzór na objętość kuli odgrywa ważną rolę w licznych dziedzinach nauki i technologii, w tym w fizyce, inżynierii, biologii oraz matematyce.

W kontekście fizyki, obliczenia objętości kuli są niezbędne przy badaniu ruchu ciał sferycznych. Na przykład, w przypadku analizy planet oraz innych obiektów kosmicznych, znajomość tego wzoru umożliwia określenie masy, jeśli dysponujemy danymi o gęstości i objętości. Ta informacja jest kluczowa w astronomii, gdzie każdy detal ma znaczenie.

W inżynierii, wykorzystanie wzoru na objętość kuli jest praktyczne w projektowaniu takich elementów jak:

zbiorniki,
kuliste pompy,
kule zaworowe.

Precyzyjne obliczenia ich objętości pozwalają na ustalenie pojemności oraz dobór odpowiednich materiałów do produkcji.

W biologii, ten wzór zyskuje znaczenie przy analizie objętości komórek i innych biologicznych struktur. Dzięki tym obliczeniom lepiej rozumiemy mechanizmy życiowe organizmów oraz ich zdolności do przystosowywania się do różnorodnych warunków środowiskowych.

W kontekście edukacji matematycznej, wzór na objętość kuli staje się świetnym przykładem do nauki geometrii przestrzennej. Daje uczniom możliwość zgłębiania właściwości kul oraz rozwijania umiejętności analitycznych.

Wszystkie te zastosowania podkreślają ogromne znaczenie wzoru na objętość kuli, który odnajduje swoje miejsce nie tylko w naukowej teorii, ale także w praktycznych aspektach codziennego życia.

Jakie przykłady obliczeń objętości kuli można spotkać?

Przykłady obliczania objętości kuli odgrywają kluczową rolę w nauczaniu geometrii, zarówno na poziomie szkoły podstawowej, jak i średniej. Te praktyczne obliczenia umożliwiają uczniom lepsze zrozumienie, w jaki sposób wymiary kuli wpływają na jej pojemność.

Rozpocznijmy od pierwszego przykładu:

Obliczamy objętość kuli o promieniu 3 cm. Korzystamy z wzoru V = (4/3)πr³, gdzie r oznacza promień. W tym przypadku obliczamy:

V = (4/3)π(3)³,
V = (4/3)π(27),
co daje nam wynik 36π cm³,
co z kolei jest bliskie 113,1 cm³.

Przejdźmy do drugiego przykładu:

Chcemy obliczyć objętość kuli, mając na uwadze pole powierzchni wynoszące 113,1 cm². Najpierw musimy znaleźć promień, korzystając z wzoru na pole powierzchni:

S = 4πr². Przekształcamy go tak, aby uzyskać promień:

r = √(S/(4π)). Po wyliczeniu promienia możemy zastosować go w wzorze na objętość.

Te przykłady jasno ilustrują, jak praktycznie można zastosować wzór na objętość kuli, przeprowadzając istotne obliczenia oraz przypominając o podstawowych definicjach promienia i średnicy. Tego rodzaju zadania są niezwykle pomocne dla uczniów, ponieważ pozwalają im lepiej zrozumieć zagadnienia związane z geometrią oraz dostrzegać ich zastosowanie w codziennym życiu.

Przykład: Obliczanie objętości kuli o promieniu 3 cm

Aby obliczyć objętość kuli o promieniu 3 cm, skorzystamy ze wzoru na tę objętość, który brzmi:

V = (4/3) × π × r³.

Podstawiając nasz promień, przeprowadzamy obliczenia:

V = (4/3) × π × (3 cm)³.

Zaczynając od wartości promienia, mamy:

V = (4/3) × π × 27 cm³, co prowadzi nas do:

V = (4/3) × 27π cm³.

Po chwili uzyskujemy wynik:

V = 36π cm³.

Zatem, objętość kuli o promieniu 3 cm wynosi 36π cm³, co możemy przybliżyć do około 113,1 cm³, jeśli przyjmiemy π jako 3,14.

Ten przykład podkreśla, jak kluczowy jest promień przy obliczaniu objętości. Używamy wzoru, aby lepiej zrozumieć, jak zachowuje się objętość w jednostkach cm³.

Przykład: Obliczenie objętości na podstawie pola powierzchni

Aby określić objętość kuli na podstawie jej pola powierzchni, wystarczy wykonać kilka prostych kroków. Rozpoczniemy od wzoru na pole powierzchni kuli, który brzmi: P = 4πr². Z tego równania możemy obliczyć promień.

Na wstępie przekształcamy wzór, aby znaleźć wartość promienia: r = √(P / 4π).
Po ustaleniu promienia, możemy przejść do obliczeń objętości kuli. Wzór na objętość ma postać V = (4/3)πr³. Tutaj podstawiamy wcześniej uzyskaną wartość promienia.

Na przykład, jeśli pole powierzchni kuli wynosi 50,24 cm², obliczymy promień w następujący sposób:

r = √(50,24 / (4π)) ≈ 2 cm.

Następnie, korzystając z promienia, wyliczamy objętość:

V = (4/3)π(2)³ ≈ 33,51 cm³.

Dzięki tym prostym wzorom i przekształceniom mamy możliwość łatwego obliczenia objętości kuli, znając jej pole powierzchni.