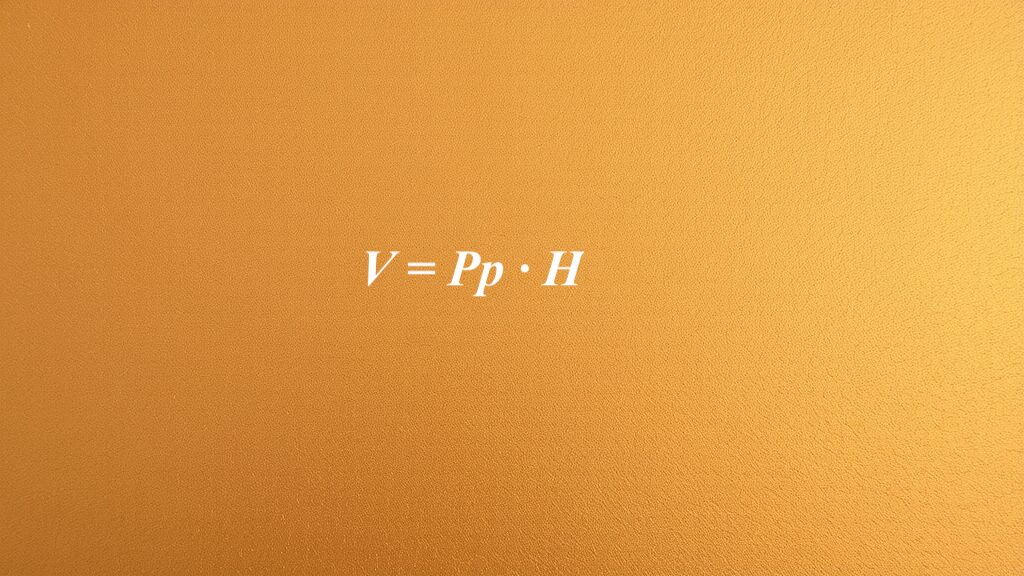Wzór na objętość graniastosłupa

Co oznacza wzór na objętość graniastosłupa?

Wzór na objętość graniastosłupa to kluczowa formuła matematyczna, która umożliwia obliczenie pojemności tej specyficznej bryły geometrycznej. Można go zdefiniować jako iloczyn pola podstawy oraz wysokości graniastosłupa. W skrócie wygląda to tak: V = Pp · H, gdzie V oznacza objętość, Pp to pole podstawy, a H to wysokość.

Pole podstawy (Pp) to powierzchnia figury, która tworzy dolną część graniastosłupa, natomiast wysokość (H) to odległość pomiędzy dwiema równoległymi podstawami, mierzona w kierunku prostopadłym. To ogólne podejście sprawia, że wzór jest bardzo wszechstronny – możemy go zastosować do obliczenia objętości różnych graniastosłupów, bez względu na kształt ich podstawy.

Dzięki temu wzorowi szybko i precyzyjnie określamy, jaką objętość zajmuje ta figura. Ma to wielkie znaczenie nie tylko w dziedzinie matematyki, ale także w geometrii oraz w zastosowaniach praktycznych, gdzie znajomość objętości ma kluczowe znaczenie.

Jak wygląda uniwersalny wzór na objętość graniastosłupa?

Objętość graniastosłupa można obliczyć, korzystając z prostego wzoru V = Pp · H. W tym równaniu V oznacza objętość, Pp odnosi się do pola podstawy, a H stanowi wysokość bryły. Ten uniwersalny wzór sprawdza się dla wszelakich graniastosłupów, niezależnie od kształtu ich podstawy – mogą to być:

• trójkąty,
• prostokąty,
• a nawet bardziej skomplikowane figury.

Wysokość H to po prostu odległość między dwiema równoległymi podstawami, co czyni obliczanie objętości szybkim i precyzyjnym procesem. Dzięki temu wzorowi możemy łatwo określić objętość różnych graniastosłupów, opierając się tylko na podstawie i wysokości.

Jakie elementy zawiera wzór na objętość graniastosłupa?

Wzór na obliczanie objętości graniastosłupa opiera się na dwóch istotnych składnikach: polu podstawy (Pp) i wysokości (H).

• pole podstawy to obszar zajmowany przez kształt geometryczny znajdujący się na dnie bryły, który może przybierać formę trójkąta,
• kwadratu,
• czy sześciokąta foremnego.

Wysokość to odległość pomiędzy dwiema równoległymi podstawami, mierzona prostopadle do nich. Możemy zapisać wzór na objętość graniastosłupa jako V = Pp · H, gdzie V oznacza poszukiwaną wartość objętości.

Zrozumienie tych dwóch aspektów jest niezwykle ważne dla właściwego obliczenia objętości graniastosłupa.

Dlaczego pole podstawy i wysokość są kluczowe?

Pole podstawy oraz wysokość graniastosłupa odgrywają kluczową rolę w obliczeniach związanych z jego objętością. Zasada jest prosta: wystarczy pomnożyć pole podstawy przez wysokość, aby uzyskać pożądany wynik.

Pole podstawy odnosi się do powierzchni figury geometrycznej, która stanowi fundament graniastosłupa. Z kolei wysokość to odległość mierzona prostopadle pomiędzy dwiema podstawami.

Dokładne określenie tych dwóch parametrów jest niezbędne, aby przeprowadzić precyzyjne obliczenia objętości. Ważne jest, by wysokość była zawsze mierzona prostopadle, niezależnie od tego, czy graniastosłup jest prosty, czy pochylony.

Wszystkie te aspekty pokazują, że pole podstawy oraz wysokość są fundamentalnymi elementami wzoru na objętość graniastosłupa. To właśnie od nich w dużej mierze zależy jakość i dokładność naszych obliczeń.

Jak obliczać pole podstawy graniastosłupa?

Pole podstawy graniastosłupa wyznacza się w zależności od jego kształtu. Może to być na przykład:

• trójkąt,
• prostokąt,
• kwadrat,
• trapez,
• sześciokąt foremny.

Każda z tych figur ma swój unikalny wzór do wyliczenia pola. Dla przykładu, aby znaleźć pole trójkąta, wystarczy obliczyć połowę iloczynu długości jego podstawy i wysokości. W przypadku prostokąta pole to po prostu iloczyn długości jego boków.

Aby dokładnie obliczyć pole podstawy, niezbędne są precyzyjne wymiary figury, w tym długości boków. Starannie wykonane obliczenia mają ogromne znaczenie, gdyż stanowią kluczowy składnik formuły do obliczenia objętości graniastosłupa: V = Pp · H, gdzie Pp oznacza pole podstawy.

W praktyce, nim przystąpimy do wyliczania objętości graniastosłupa, warto najpierw szczegółowo określić pole jego podstawy, dostosowując metodykę do specyfiki danego kształtu.

Jak pole podstawy zależy od typu figury geometrycznej?

Pole podstawy różni się w zależności od kształtu figury geometrycznej, która je tworzy. Oto jak obliczyć pole dla różnych kształtów:

• Trójkąt: pole obliczamy, mnożąc długość podstawy przez wysokość, a następnie dzieląc przez dwa.
• Kwadrat: pole to długość boku podniesiona do kwadratu.
• Prostokąt: pole uzyskujemy, mnożąc długości dwóch sąsiednich boków.
• Trapez: pole oblicza się, mnożąc wysokość przez połowę sumy długości obu podstaw.
• Sześciokąt foremny: pole obliczamy według wzoru: 6 razy (a kwadrat razy pierwiastek z 3, podzielony przez 4), gdzie a to długość boku figury.

Wybór odpowiedniego wzoru jest kluczowy dla precyzyjnego obliczenia pola podstawy graniastosłupa.

Jak wyznaczyć pole podstawy graniastosłupa trójkątnego?

Pole podstawy trójkątnego graniastosłupa można ustalić poprzez obliczenie pola trójkąta, który jest jego podstawą. W przypadku prostokątnego trójkąta, pole obliczamy jako połowę iloczynu długości jego dwóch przyprostokątnych. Można to zapisać w formie równania:

P = (1/2) · a · b,

gdzie a oraz b oznaczają długości tych przyprostokątnych.

Natomiast dla trójkąta równobocznego stosujemy inny wzór:

P = (√3/4) · a²,

gdzie a to długość boku trójkąta.

Precyzyjne obliczenie pola podstawy jest niezwykle istotne, gdyż ma kluczowe znaczenie dla dalszych analiz oraz obliczeń objętości graniastosłupa trójkątnego. Zrozumienie tej kalkulacji pomoże lepiej zgłębić właściwości tego typu bryły.

Jak wyznaczyć pole podstawy graniastosłupa prostokątnego?

Aby obliczyć pole podstawy graniastosłupa prostokątnego, stosujemy tę samą metodę, co w przypadku prostokąta – wystarczy pomnożyć długość dwóch przyległych boków. Na przykład, dla podstawy o wymiarach 5 cm i 3 cm, rezultatem będzie 15 cm².

W przypadku prostopadłościanu, który możemy traktować jako szczególny typ graniastosłupa prostokątnego, zasada pozostaje niezmienna. Po prostu mnożymy długość przez szerokość. Precyzyjne zmierzenie tych boków odgrywa kluczową rolę, ponieważ umożliwia późniejsze obliczenie objętości. Aby to zrobić, wystarczy pomnożyć pole podstawy przez wysokość graniastosłupa. Dzięki temu zyskujemy dokładny obraz zarówno pola powierzchni, jak i objętości tej bryły.

Jak obliczyć pole podstawy graniastosłupa prawidłowego sześciokątnego?

Pole podstawy graniastosłupa prawidłowego sześciokątnego można łatwo obliczyć, korzystając ze wzoru na pole sześciokąta foremnego. Ten wzór brzmi: 6 · (a²√3/4), gdzie „a” to długość krawędzi podstawy.

Sześciokąt foremny wyróżnia się równymi bokami oraz identycznymi kątami wewnętrznymi, co ułatwia zastosowanie formuły. Gdy już obliczymy pole podstawy, możemy je wykorzystać do przeprowadzenia kolejnych obliczeń, na przykład objętości graniastosłupa. Aby to zrobić, należy:

1. pomnożyć pole podstawy przez wysokość bryły.

Warto pamiętać, że ten wzór odnosi się wyłącznie do graniastosłupów, których podstawą jest foremny sześciokąt.

W jakich sytuacjach stosuje się twierdzenie Pitagorasa?

Twierdzenie Pitagorasa jest niezwykle pomocne w obliczaniu długości krawędzi, wysokości oraz przekątnych graniastosłupów, zwłaszcza gdy ich podstawy lub ściany boczne tworzą kąty prostokątne. To narzędzie staje się nieocenione, gdy chcemy ustalić wysokość graniastosłupa pochyłego albo długości krawędzi bocznych, które nie są prostopadłe do podstawy.

Z wiedzą na temat długości dwóch boków trójkąta prostokątnego, mamy możliwość łatwego wyznaczenia długości trzeciego boku. Dzięki temu twierdzeniu możemy precyzyjnie określić wymiary obiektów, co jest kluczowe dla późniejszych obliczeń, takich jak:

• obliczanie objętości,
• obliczanie powierzchni graniastosłupa.

Takie podejście zwiększa dokładność naszych wyliczeń oraz upraszcza proces, którym się zajmujemy.

Jak ustalić wysokość graniastosłupa?

Wysokość graniastosłupa odnosi się do odległości między jego dwiema równoległymi podstawami, która jest mierzona prostopadle do nich. W przypadku prostego graniastosłupa, ta wartość odpowiada długości krawędzi bocznej, a więc linii, która jest ustawiona prostopadle do podstawy. Natomiast w graniastosłupach pochylonych wysokość również definiuje się jako odległość między podstawami, ale ważne jest, że mierzona jest w linii prostej, bez względu na kąt nachylenia bocznych krawędzi.

Precyzyjne ustalenie wysokości odgrywa kluczową rolę w obliczaniu objętości graniastosłupa. Wartość ta ma istotny wpływ na całkowitą pojemność obiektu, dlatego nie należy jej lekceważyć.

W których przypadkach wysokość to długość krawędzi bocznej?

Wysokość graniastosłupa jest równa długości krawędzi bocznej jedynie w przypadku graniastosłupów prostych. W takich bryłach krawędzie boczne są ustawione prostopadle do podstawy, a ściany, które je łączą, przyjmują formę prostokątów. W graniastosłupach pochyłych sytuacja jest jednak inna, ponieważ krawędzie boczne nie są prostopadłe do podstawy. W związku z tym wysokość definiuje się jako odległość prostopadłą między podstawami, co skutkuje tym, że nie odpowiada ona długości krawędzi bocznej.

Warto zapamiętać, że wysokość zawsze odnosi się do odcinka prostopadłego względem podstawy, co ma ogromne znaczenie przy obliczaniu objętości każdego graniastosłupa.

Jak krok po kroku obliczać objętość graniastosłupa?

Aby obliczyć objętość graniastosłupa, w pierwszej kolejności musimy zidentyfikować kształt jego podstawy. Kluczowe jest też wyznaczenie pola powierzchni tej podstawy, co można osiągnąć za pomocą odpowiednich wzorów, zależnych od rodzaju figury geometrycznej. Na przykład, dla:

• trójkątów,
• prostokątów,
• sześciokątów.

Każda z tych figur wymaga innych formuł.

Kolejnym krokiem jest zmierzenie wysokości graniastosłupa, która definiuje odległość prostopadłą między górną a dolną podstawą. Ważne, aby wszystkie dokonywane pomiary, zarówno pole podstawy, jak i wysokość, były w tych samych jednostkach – czy to centymetrach, czy może w metrach.

Kiedy upewnimy się, że jednostki są spójne, możemy przystąpić do obliczeń, stosując wzór: V = pole podstawy × wysokość graniastosłupa. Wynik, jaki uzyskujemy, będzie w jednostkach sześciennych, takich jak centymetry sześcienne (cm³) lub metry sześcienne (m³).

Taki przemyślany i systematyczny sposób obliczania objętości graniastosłupa znajduje zastosowanie w różnych sytuacjach.

Jak sprawdzić jednostki przy obliczaniu objętości?

Aby poprawnie obliczyć objętość graniastosłupa, pierwszym krokiem jest upewnienie się, że długość, szerokość oraz wysokość są podane w tych samych jednostkach. Mogą to być metry, decymetry lub centymetry. Objętość wyrażamy w jednostkach sześciennych, które zgadzają się z wybraną długością, na przykład w metrach sześciennych (m³), decymetrach sześciennych (dm³) lub centymetrach sześciennych (cm³).

Zanim jednak przystąpisz do obliczeń, warto zamienić jednostki, jeśli nie są zgodne. Dzięki temu możesz uniknąć ewentualnych pomyłek. Przydatne jest także posiadanie wiedzy o jednostkach pojemności. Przykładowo:

• 1 dm³ jest równy liter,
• 0,001 dm³ to mililitr,
• hektolitr to 100 dm³,
• baryłka ma różne wartości w zależności od przeznaczenia.

Znajomość tych jednostek ułatwia przeliczanie wyników objętości na bardziej praktyczne miary.

Jak wykonać rysunek pomocniczy?

Rysunek pomocniczy pomaga w lepszym zobrazowaniu graniastosłupa i upraszcza proces obliczania jego objętości. Proces rozpoczynamy od:

• narysowania podstawy figury,
• dokładnego określenia wymiarów boków,
• uwzględnienia wysokości graniastosłupa,
• długości krawędzi bocznych.

W przypadku graniastosłupów pochylonych warto również:

• zaznaczyć przekątne,
• określić kąty między krawędziami.

Takie przygotowanie ma ogromne znaczenie, gdy przystępujemy do kalkulacji objętości. Ostatecznie, posługiwanie się takim rysunkiem pozwala na łatwiejsze stosowanie odpowiednich wzorów oraz minimalizuje ryzyko błędów podczas pomiarów.

Przykład obliczenia objętości różnych typów graniastosłupów

Obliczanie objętości prostego graniastosłupa o prostokątnej podstawie jest niewątpliwie łatwe. Wystarczy pomnożyć pole prostokąta, które uzyskujemy z długości i szerokości, przez wysokość graniastosłupa. Na przykład, kiedy mamy prostokąt o wymiarach 4 metry na 3 metry i wysokości 5 metrów, objętość wynosi 4 razy 3 razy 5, co daje 60 metrów sześciennych.

Przechodząc do graniastosłupa trójkątnego, aby obliczyć pole podstawy, musimy pomnożyć długości dwóch przyprostokątnych i podzielić przez dwa. Dla przyprostokątnych o długości 6 metrów i 4 metrów oraz wysokości graniastosłupa wynoszącej 10 metrów, objętość obliczamy jako 0,5 razy 6 razy 4 razy 10, co daje nam 120 metrów sześciennych.

Gdy mówimy o graniastosłupie prawidłowym sześciokątnym, korzystamy ze wzoru na pole sześciokąta foremnego, który brzmi: P = (3√3 / 2) × a², gdzie a to długość boku podstawy. Dla boku o długości 2 metrów i wysokości 8 metrów, obliczenia prowadzą nas do objętości: V = P × H = (3√3 / 2) × 2² × 8, co w rezultacie daje nam około 83,14 metrów sześciennych.

Te przykłady doskonale ilustrują, jak stosować uniwersalny wzór V = Pp × H do obliczania objętości dla różnych typów graniastosłupów. Dzięki nim widzimy, jak zróżnicowane mogą być obliczenia geometryczne.

Na czym polega różnica między objętością graniastosłupa prostego a pochyłego?

Różnice w objętości graniastosłupa prostego i pochyłego wynikają głównie z układu ich krawędzi bocznych w odniesieniu do podstawy. W graniastosłupach prostych krawędzie boczne są ustawione prostopadle do podstawy, co oznacza, że wysokość graniastosłupa jest równa długości tych krawędzi. Z kolei w graniastosłupach pochyłych krawędzie boczne mają kąt nachylenia, co sprawia, że wysokość definiuje się jako miara prostopadła między podstawami, a nie jako długość krawędzi bocznej.

Mimo tych różnic, sposób obliczania objętości pozostaje taki sam dla obu rodzajów graniastosłupów: objętość obliczamy jako pole podstawy pomnożone przez wysokość. Wysokość zawsze odnosi się do odległości mierzonych prostopadle pomiędzy podstawami. To fundamentalna zasada, której przestrzeganie jest kluczowe dla prawidłowego wyznaczenia objętości, niezależnie od tego, czy mamy do czynienia z graniastosłupem prostym, czy pochyłym.

Jakie są zasady zamiany jednostek objętości?

Zasady dotyczące zamiany jednostek objętości opierają się na przeliczeniach między jednostkami sześciennymi a pojemnościowymi. Na przykład, jeden metr sześcienny (m³) odpowiada tysiącu decymetrów sześciennych (dm³). Co ciekawe, każdy dm³ jest równy jednemu litrowi (l), co sprawia, że konwersja objętości z dm³ na litry jest niezwykle prosta.

Kiedy przekształcamy jednostki, na przykład z litrów na mililitry, stosujemy prostą zasadę: jeden litr to 1000 mililitrów (ml). Hektolitr (hl) z kolei odpowiada 100 litrom. Istnieje również baryłka, która stanowi większą jednostkę objętości, często używaną w przemyśle naftowym oraz piwowarskim; jej pojemność zazwyczaj wynosi około 159 litrów, ale może się różnić w zależności od kontekstu.

Warto zauważyć, że przy konwersji jednostek sześciennych istotne jest uwzględnienie potęgowania długości. Długość jednego metra jest równa 10 decymetrom, dlatego objętość 1 m³ to (10 dm)³, co przekłada się na 1000 dm³. Taki sposób myślenia ułatwia i precyzuje przemiany między różnymi jednostkami objętości.

Aby skutecznie zamieniać jednostki objętości, warto kierować się kilkoma prostymi zasadami:

• przy przeliczeniach między m³, dm³ i l należy mnożyć lub dzielić przez 1000,
• na przykład, aby zamienić litry na mililitry, wystarczy pomnożyć przez 1000,
• hektolitry przeliczamy na litry, mnożąc przez 100,
• należy również pamiętać o specyfice jednostek niestandardowych, jak baryłka.

Przestrzeganie tych zasad gwarantuje, że obliczenia związane z objętością będą zarówno spójne, jak i precyzyjne.

Jak zamieniać decymetry sześcienne, litry, mililitry, metry sześcienne, baryłki i hektolitry?

Decymetr sześcienny (dm³) jest równy dokładnie jednemu litrowi (l). Warto dodać, że litr to 1000 mililitrów (ml). Metr sześcienny (m³) składa się z 1000 decymetrów sześciennych, co przekłada się na 1000 litrów. Z kolei hektolitr (hl) stanowi równowartość 100 litrów.

Aby zamieniać jednostki, posługujemy się odpowiednimi współczynnikami. Na przykład:

• przeliczenie metrów sześciennych na litry wymaga pomnożenia przez 1000,
• konwersja litrów na decymetry sześcienne odbywa się w stosunku 1:1.

Baryłki, które mogą mieć różne pojemności w zależności od ich przeznaczenia, zazwyczaj zawierają około 159 litrów. Kiedy dokonujemy zamiany jednostek objętości, kluczowe jest uwzględnianie różnych skal. Należy pamiętać o mnożeniu lub dzieleniu przez potęgi dziesięciu, zwracając uwagę na proporcje między jednostkami sześciennymi a pojemnościowymi.

Jak wykorzystać wiedzę o objętości graniastosłupa na egzaminie ósmoklasisty?

Wiedza na temat objętości graniastosłupa odgrywa bardzo istotną rolę w przygotowaniach do egzaminu ósmoklasisty. Umożliwia sprawne rozwiązywanie problemów związanych z geometrią przestrzenną. Aby właściwie obliczyć objętość graniastosłupa, posługujemy się wzorem: V = Pp · H, gdzie Pp oznacza pole podstawy, a H to jego wysokość.

Niezwykle istotne jest, aby znać metody wyliczania pola podstawy dla rozmaitych figur, takich jak:

• trójkąty,
• prostokąty,
• sześciokąty foremne.

To pozwala na dokładne przeprowadzanie obliczeń. Ważne jest również, aby poprawnie zdefiniować wysokość oraz śledzić jednostki miar, co pomaga uniknąć różnych pomyłek.

Dobrze jest także narysować szkic, który pomoże zobrazować problem i ułatwi zastosowanie twierdzenia Pitagorasa, by określić brakujące długości. Umiejętność przeliczania jednostek objętości, na przykład dm³, l czy m³, znacznie poszerza nasze możliwości działania.

Systematyczne ćwiczenia oraz praktyczne przykłady przyczyniają się do głębszego zrozumienia tych tematów. W ten sposób stajemy się coraz lepsi i bardziej pewni siebie podczas egzaminu ósmoklasisty.