Objętość przedmiotu można wyznaczyć, dzieląc jego masę przez gęstość, zgodnie ze wzorem V = m/ρ. W przypadku regularnych brył wykorzystuje się specjalne wzory geometryczne, które umożliwiają szybkie i dokładne obliczenia. Natomiast w sytuacji, gdy kształt jest nieregularny, często stosuje się metodę Archimedesa, pozwalającą na precyzyjne określenie objętości. Znajomość tych zasad jest niezwykle istotna, ponieważ umożliwia dokładne pomiary oraz efektywne wykorzystanie materiałów.
Co to jest objętość i jak ją obliczyć?
Objętość określa przestrzeń zajmowaną przez trójwymiarowy obiekt i zazwyczaj wyraża się ją w jednostkach sześciennych, takich jak metry czy centymetry sześcienne. W przypadku prostych figur, na przykład prostopadłościanu, wystarczy pomnożyć długość, szerokość i wysokość, by obliczyć objętość. Gdy natomiast mamy do czynienia z bardziej złożonymi kształtami, jak kula czy stożek, stosuje się specjalne wzory matematyczne umożliwiające precyzyjne określenie zajmowanej przez nie przestrzeni. W układzie SI podstawową miarą objętości jest metr sześcienny (m³).
Jakie są wzory na objętość najważniejszych brył geometrycznych?
Wzory na obliczanie objętości różnych brył geometrycznych różnią się w zależności od ich kształtu oraz wymiarów.
Na przykład:
- objętość sześcianu obliczamy jako V = a³, gdzie „a” to długość krawędzi,
- objętość prostopadłościanu to V = a × b × c, gdzie „a” to długość, „b” to szerokość, a „c” to wysokość,
- objętość walca znajduje się poprzez V = π r² h, gdzie „r” to promień podstawy, a „h” to wysokość,
- objętość kuli określamy równaniem V = (4/3) π r³, gdzie „r” to promień sfery,
- objętość graniastosłupa uzyskujemy jako V = P_p h, gdzie P_p to pole podstawy,
- objętość stożka wynosi V = (1/3) π r² h, a objętość ostrosłupa to V = (1/3) P_p h.
Te wzory są nieocenionymi narzędziami w matematyce, umożliwiającymi obliczanie objętości różnych brył na podstawie wymiarów, takich jak długość, szerokość, wysokość, promień oraz pole podstawy.
Wzór na objętość sześcianu
Objętość sześcianu można obliczyć przy zastosowaniu prostego wzoru:
V = a³, gdzie „a” reprezentuje długość krawędzi. Wszystkie krawędzie sześcianu są równe, co sprawia, że wystarczy podnieść tę wartość do potęgi trzeciej, aby uzyskać objętość.
Ten wzór nie tylko jest łatwy do zrozumienia, ale również znajduje szerokie zastosowanie w:
- problemach matematycznych,
- praktycznych obliczeniach,
- przestrzeni trójwymiarowej.
Wzór na objętość prostopadłościanu
Objętość prostopadłościanu można obliczyć stosując wzór: V = a × b × c. W tym przypadku „a” oznacza długość, „b” to szerokość, a „c” odnosi się do wysokości bryły. Prostopadłościan to figura geometryczna z prostymi krawędziami i prostokątnymi podstawami, co czyni go łatwym do zrozumienia.
Aby określić objętość, wystarczy pomnożyć trzy wymiary. Wynik, czyli pojemność prostopadłościanu, podawany jest w jednostkach objętości, takich jak metry sześcienne czy litry.
Dzięki temu wzorowi możemy szybko i skutecznie obliczać objętość różnych prostopadłościanów, biorąc pod uwagę ich specyficzne wymiary. To prosty sposób, który ułatwia zrozumienie i realizację obliczeń.Wzór na objętość walca
Objętość walca można obliczyć przy użyciu wzoru V = π r² h. W tym równaniu r oznacza promień podstawy, a h jest wysokością walca. Pole podstawy walca, które przyjmuje formę koła, wynosi π r².
Aby obliczyć objętość, traktujemy pole podstawy jako kluczowy składnik, który następnie mnożymy przez wysokość. Taki sposób obliczeń zapewnia dokładność w analizach geometrycznych. Wzór na objętość walca znajduje zastosowanie nie tylko w teorii matematycznej, ale również w rozmaitych praktycznych dziedzinach inżynieryjnych. Dzięki niemu możemy łatwo określić objętość każdego walca, dla którego znamy promień i wysokość.
Wzór na objętość kuli
Wzór na objętość kuli brzmi V = (4/3) π r³. W tej formuły r symbolizuje promień kuli, a π to stała matematyczna o przybliżonej wartości 3,14159. Obliczając objętość, najpierw podnosimy promień do potęgi trzeciej, a następnie mnożymy wynik przez cztery trzecie oraz π.
Ten wzór odgrywa kluczową rolę w dziedzinie geometrii, fizyki i wielu innych naukach, umożliwiając precyzyjne określenie objętości kuli, która jest symetryczna w każdej płaszczyźnie. Oznacza to, że jej objętość zależy wyłącznie od długości promienia.
Znajomość tego wzoru otwiera drzwi do rozwiązywania wielu praktycznych problemów związanych z pomiarami objętości obiektów kulistych. Możemy go zastosować do:
- obliczeń dotyczących sportowych piłek,
- obliczeń kul towarzyskich,
- procesów inżynieryjnych,
- projektowania różnorodnych konstrukcji,
- efektywnego tworzenia i analizowania obiektów.
Wzór na objętość graniastosłupa
Objętość graniastosłupa można obliczyć za pomocą wzoru: V = P_p * h. W tym równaniu P_p oznacza pole podstawy, natomiast h to wysokość graniastosłupa. Graniastosłup to figura geometryczna składająca się z dwóch równoległych podstaw oraz ścian bocznych w postaci prostokątów lub równoległoboków.
Z powyższego wzoru wynika, że objętość graniastosłupa jest uzależniona zarówno od powierzchni podstawy, jak i od jego wysokości. Ta forma obliczeń przypomina wzór na objętość walca, w którym podstawą jest okrąg. W praktyce pole podstawy oblicza się w zależności od kształtu—przykładowo, może to być:
- trójkąt,
- prostokąt,
- wielokąt.
Dodatkowo, uwzględnienie wysokości graniastosłupa umożliwia dokładne określenie jego objętości. Wzory te są niezwykle istotne w geometrii, a ich zastosowanie znajduje się także w takich dziedzinach jak inżynieria czy budownictwo.
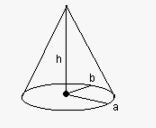
Wzór na objętość stożka
Objętość stożka można wyznaczyć za pomocą wzoru: V = (1/3) π r² h. Tutaj r oznacza promień podstawy, a h to jego wysokość. Pole podstawy, która ma kształt koła o promieniu r, można przedstawić jako π r².
Interesujące jest to, że objętość stożka to zaledwie jedna trzecia objętości walca o identycznej podstawie i wysokości. Ten wzór jest niezwykle istotny w geometrii, ponieważ pozwala nam oszacować, jaką przestrzeń zajmuje ta ciekawa figura o okrągłej podstawie.
Wzór na objętość ostrosłupa
Objętość ostrosłupa można obliczyć przy pomocy wzoru: V = (1/3) P_p h. W tym wzorze P_p oznacza pole podstawy, natomiast h to wysokość, czyli odległość od wierzchołka do płaszczyzny podstawy. Ostrosłup to solidna figura, której podstawa ma kształt wielokąta, a wierzchołek znajduje się powyżej tej podstawy.
Wzór ten odgrywa istotną rolę w obliczaniu objętości różnych ostrosłupów, niezależnie od kształtu ich podstaw. Zauważ, że jest on analogiczny do wzoru stosowanego dla stożków, z tą różnicą, że dotyczy podstaw wielokątnych, a nie tylko okrągłych. Biorąc pod uwagę pole podstawy oraz wysokość, możemy precyzyjnie obliczyć objętość danej bryły.
| Bryła geometryczna | Wzór na objętość | Opis parametrów |
|---|---|---|
| Sześcian | V = a³ | a – długość krawędzi |
| Prostopadłościan | V = a × b × c | a – długość, b – szerokość, c – wysokość |
| Walec | V = π r² h | r – promień podstawy, h – wysokość |
| Kula | V = (4/3) π r³ | r – promień kuli |
| Graniastosłup | V = P_p × h | P_p – pole podstawy, h – wysokość |
| Stożek | V = (1/3) π r² h | r – promień podstawy, h – wysokość |
| Ostrosłup | V = (1/3) P_p × h | P_p – pole podstawy, h – wysokość |
Od jakich parametrów zależy objętość bryły?
Objętość bryły w dużej mierze zależy od jej wymiarów oraz kształtu. Kluczowymi czynnikami są:
- pole podstawy,
- wysokość,
- promień,
- średnica.
To szczególnie ważne w przypadku takich figur jak graniastosłupy, walce, stożki oraz ostrosłupy. W kulach i cylindrach główną rolę odgrywają promień i średnica.
Dla sześcianów i prostopadłościanów objętość obiektów wyznacza:
- długość krawędzi,
- szerokość,
- wysokość.
Zmiany tych wymiarów wpływają na objętość w sposób proporcjonalny do sześcianu skali, co oznacza, że nawet drobne modyfikacje mogą znacznie wpłynąć na objętość.
Zasada Cavalierego umożliwia porównywanie objętości brył o identycznych przekrojach. Głosi ona, że jeżeli przekroje poprzeczne dwóch brył mają taki sam kształt i pole, to ich objętości są równe, nawet jeśli różnią się innymi wymiarami.
W praktyce, kluczowe parametry, takie jak:
- pole podstawy,
- wysokość,
- promień,
- średnica,
- długość krawędzi,
determinują objętość danej figury geometrycznej.
Pole podstawy i wysokość
Pole podstawy oraz wysokość to istotne elementy przy obliczaniu objętości różnorodnych brył geometrycznych. Aby ustalić objętość graniastosłupa lub walca, należy pomnożyć pole podstawy przez ich wysokość. W przypadku stożków oraz ostrosłupów sytuacja wygląda nieco inaczej, ponieważ objętość tych figur wynosi jedną trzecią iloczynu pola podstawy i wysokości.
Warto zwrócić uwagę, że kształt podstawy wpływa na pole. Na przykład:
- gdy mamy do czynienia z podstawą okrągłą, pole obliczamy na podstawie wzoru na pole koła,
- dla graniastosłupów o podstawach wielokątnych posługujemy się wzorem na pole wielokąta.
Wysokość bryły definiuje odległość, mierzoną prostopadle, od podstawy do przeciwległej ściany lub wierzchołka.
Zrozumienie tych dwóch kluczowych parametrów jest niezbędne do dokładnego obliczania objętości różnych brył. Stanowi to podstawowy element geometrii, który znajduje zastosowanie w wielu dziedzinach życia codziennego oraz w praktycznych zastosowaniach.
Jakie są jednostki objętości i jak je przeliczać?
Jednostki miary objętości pozwalają nam określić, jaką przestrzeń zajmują różne obiekty. W systemie SI podstawowym wymiarem jest metr sześcienny (m³), co odpowiada objętości sześcianu o krawędzi wynoszącej 1 metr. Obok tej jednostki istnieją także mniejsze miary, takie jak decymetr sześcienny (dm³) oraz centymetr sześcienny (cm³), które są odpowiadające litrom i mililitrom.
Decymetr sześcienny, czyli 1 dm³, jest równy 1 litrze (l); to właśnie ta jednostka najczęściej stosuje się do pomiarów objętości cieczy. Z kolei centymetr sześcienny (cm³) jest równy 1 mililitrowi (ml), który zyskuje dużą popularność w medycynie i branży spożywczej.
Przeliczanie jednostek objętości opiera się na systemie dziesiętnym, co można zaprezentować w prosty sposób:
- 1 m³ to 1000 dm³, co odpowiada 1000 litrom,
- 1 dm³ to równocześnie 1000 cm³, czyli 1000 mililitrom.
Te przejrzyste przeliczenia ułatwiają konwersję między różnymi jednostkami. Dzięki temu, zarówno w naukach ścisłych, jak i w codziennych sytuacjach, można łatwo przeliczać objętości. Dla przykładu, można zmierzyć ilość cieczy w litrach, a następnie z łatwością zmienić tę wartość na centymetry sześcienne.
Jak obliczyć objętość w fizyce i chemii?
Objętość to kluczowy koncept w fizyce i chemii, często ustalana za pomocą wzoru V = m/ρ. W tym równaniu V reprezentuje objętość, m oznacza masę, a ρ to gęstość danej substancji. Dzięki temu wzorowi możemy łatwo obliczać objętość zarówno ciał stałych, jak i cieczy, o ile znamy ich masę i gęstość.
Kiedy mówimy o gazach, objętość staje się bardziej skomplikowana, ponieważ zależy od takich czynników jak:
- temperatura,
- ciśnienie,
- forma naczynia.
Dlatego do obliczeń często wykorzystuje się równanie gazu idealnego, które integruje te różne parametry. Pomiar objętości cieczy zazwyczaj przeprowadza się przy pomocy naczyń oznaczonych podziałką. Natomiast aby określić objętość nieregularnych ciał stałych, można zastosować metodę Archimedesa, polegającą na zanurzeniu obiektu w cieczy i zmierzeniu objętości wypieranej przez niego.
Zrozumienie wzoru V = m/ρ oraz zasad pomiaru objętości gazów, cieczy i ciał stałych jest niezwykle istotne w kontekście precyzyjnych obliczeń i praktycznych zastosowań w obszarze fizyki oraz chemii.
Jak wyznaczyć objętość nieregularnych obiektów?
Objętość nieregularnych kształtów można określić za pomocą metody Archimedesa, która polega na zanurzeniu obiektu w cieczy. Gdy przedmiot zostanie umieszczony w wodzie, mierzona jest ilość wypartej cieczy, a ta wartość jest równa objętości badanego obiektu.
Ta technika staje się szczególnie przydatna, gdy tradycyjne wzory geometrii nie sprawdzają się z powodu krzywizn czy skomplikowanych form ciała. Dzięki niej, pomiar objętości staje się nie tylko dokładny, ale także znalazł zastosowanie w różnych dziedzinach, w tym:
- fizyce,
- badaniach naukowych,
- kontrolowaniu objętości materiałów,
- eksperymentach.
Jak wykorzystać objętość w praktyce?
Obliczanie objętości jest niezwykle istotne w wielu codziennych zastosowaniach, zwłaszcza w budownictwie oraz technice instalacyjnej. Umiejętność ta pozwala na dokładne określenie, ile betonu będzie potrzebne do wylewek, fundamentów czy stropów, co z kolei przyczynia się do redukcji kosztów i minimalizacji strat materiałów.
W przypadku materiałów sypkich, takich jak piasek czy żwir, znajomość objętości jest kluczowa przy planowaniu wykopów i nasypów. Dzięki tym informacjom prace ziemne stają się bardziej precyzyjne i efektywne.
Jeśli mowa o wykończeniach wnętrz czy ocieplaniu budynków, wiedza o objętości nabiera jeszcze większego znaczenia. Pozwala precyzyjnie oszacować ilości:
- pianki,
- styropianu,
- wełny mineralnej.
W transporcie materiałów, objętość wpływa na wybór odpowiedniej pojemności pojazdów czy kontenerów, co jest kluczowe dla płynności operacji.
Ponadto, objętość pomieszczeń ma fundamentalne znaczenie przy projektowaniu systemów wentylacyjnych i klimatyzacyjnych. Umożliwia to określenie przepływu powietrza, który jest niezbędny do utrzymania komfortu i zdrowia użytkowników.
W kontekście konstrukcji zbiorników i szamb, precyzyjne wyliczenie objętości zapewnia odpowiednią pojemność do magazynowania cieczy czy odpadów, co jest kluczowe dla bezpieczeństwa i wydajności instalacji.
Jak wyznaczyć objętość za pomocą całek?
Objętość bryły można obliczyć, integrując funkcje, które wyznaczają jej granice w przestrzeni. W przypadku bardziej złożonych kształtów, konieczne staje się zastosowanie całki potrójnej, biorąc pod uwagę zmienne x, y i z. Ta technika pozwala na dokładne uchwycenie objętości obszaru zdefiniowanego przez powierzchnie ograniczające bryłę.
Dla obiektów o symetrii kołowej, takich jak stożki czy paraboloidy, zaleca się wykorzystanie współrzędnych biegunowych. Dzięki nim obliczenia stają się prostsze, gdyż zmieniają one dziedzinę całkowania na obszar kołowy. Taka zmiana często ułatwia identyfikację obszaru całkowania oraz wykonanie później całki podwójnej lub potrójnej.
Całka podwójna ma zastosowanie przy wyznaczaniu objętości bryły znajdującej się między dwiema funkcjami w trzech wymiarach. Proces integracji pola powierzchni odbywa się wzdłuż zdefiniowanego obszaru na płaszczyźnie. Wybór odpowiedniego obszaru całkowania odgrywa kluczową rolę, ponieważ wyznacza granice integracji, co wpływa na wyniki obliczeń.
Całki podwójne i potrójne stanowią precyzyjne narzędzie matematyczne, które pozwala na obliczanie objętości brył ograniczonych powierzchniami. Odgrywają one istotną rolę, zwłaszcza gdy kształt bryły jest nieregularny lub wymaga uwzględnienia zmienności w trzech wymiarach. Stosowanie współrzędnych biegunowych oraz prawidłowe określenie obszaru całkowania przyczyniają się do zwiększenia efektywności i dokładności tych obliczeń.