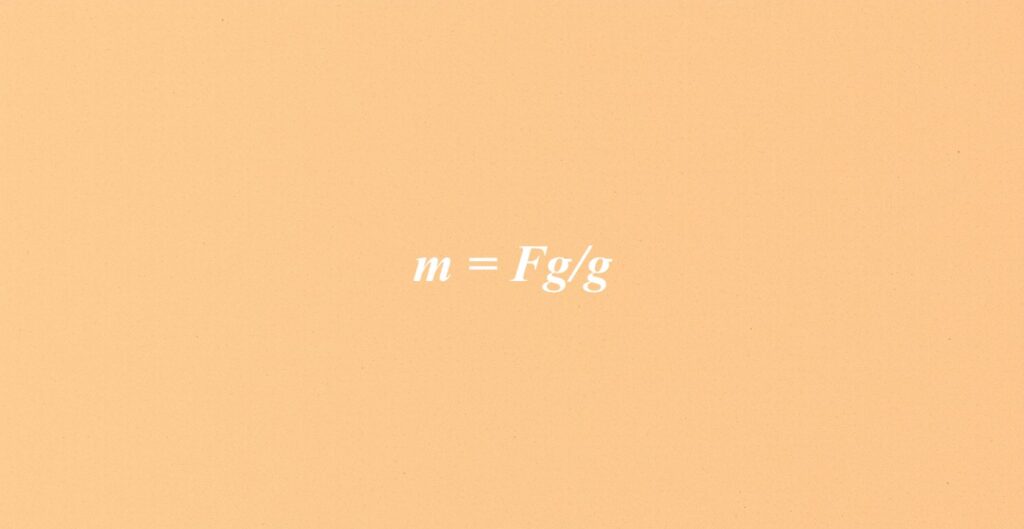Wzór na masę

Czym jest masa i jak ją definiujemy?

Masa to kluczowa wielkość fizyczna, która określa ilość materii zawartej w obiekcie. Jako wielkość skalarna dysponuje jedynie wartością liczbową, co oznacza, że nie jest uzależniona od układu odniesienia. W ramach fizyki klasycznej wyróżniamy dwa podstawowe typy masy:

• masę bezwładną, która odzwierciedla opór, jaki dany obiekt stawia wobec zmian swojego ruchu, które są rezultatem działania zewnętrznych sił,
• masę grawitacyjną, która dotyczy siły grawitacyjnej działającej między ciałami; większa masa skutkuje silniejszym oddziaływaniem.

Fundamentalna zasada równoważności masy bezwładnej i grawitacyjnej ma kluczowe znaczenie w nowoczesnej fizyce, gdyż jest niezbędna do zrozumienia dynamiki ruchu oraz teorii grawitacji.

Masa może być wyrażana w różnych jednostkach. Najczęściej spotykane to:

• kilogramy,
• gramy,
• tony.

Te podstawowe jednostki masy mają ogromne znaczenie w naukach przyrodniczych oraz engineeringu. Znacząca dokładność pomiarów masy jest niezbędna w wielu dziedzinach zastosowań.

Jakie są podstawowe wzory na masę?

Podstawowe wzory dotyczące masy odgrywają kluczową rolę w dziedzinie fizyki, umożliwiając obliczanie masy obiektów na podstawie innych wielkości. Najważniejszym z tych równań jest m = V · d. W tej formule „m” symbolizuje masę, „V” odnosi się do objętości, a „d” oznacza gęstość. Dzięki temu wzorowi bez trudu możemy ustalić masę substancji, pod warunkiem, że znamy jej objętość oraz gęstość. To narzędzie znajduje szerokie zastosowanie w naukach przyrodniczych.

Kolejnym istotnym równaniem jest m = Fg/g, gdzie „Fg” odpowiada za siłę ciężkości działającą na obiekt, a „g” to przyspieszenie grawitacyjne. To równanie umożliwia obliczenie masy, gdy dysponujemy wartością siły ciężkości. Jego przydatność szczególnie ujawnia się w kontekście badań i eksperymentów fizycznych.

Zrozumienie tych wzorów jest kluczowe nie tylko w aspekcie teoretycznym, ale także praktycznym. Wykorzystuje się je w różnorodnych dziedzinach, takich jak:

• laboratoria,
• budownictwo,
• inżynieria.

Dodatkowo, znajomość przekształceń, na przykład d = m/V, jest równie ważna, ponieważ pozwala badać gęstość substancji, gdy posiadamy informacje o masie i objętości.

Wzór: m = V * d

Wzór m = V * d to fundamentalne równanie fizyczne, które umożliwia obliczenie masy danego obiektu, odwołując się do jego objętości i gęstości. W tej formule:

• m reprezentuje masę,
• V oznacza objętość ciała,
• d to gęstość, definiowana jako stosunek masy do objętości.

Objętość możemy wyrazić w litrze lub metrach sześciennych, a gęstość zazwyczaj podaje się w kilogramach na metr sześcienny (kg/m³). Dzięki temu wzorowi, łatwo obliczymy masę, znając objętość i gęstość konkretnego przedmiotu.

Wykorzystanie wzoru m = V * d jest niezwykle wszechstronne i przydatne w wielu dziedzinach, takich jak inżynieria, chemia czy fizyka. Umożliwia on wykonywanie szybkich i precyzyjnych obliczeń, co sprawia, że jest to kluczowe narzędzie w analizie właściwości materiałów. Na przykład, można łatwo określić masę cieczy znajdującej się w zbiorniku, bazując na jego objętości oraz znanej gęstości cieczy.

Wzór: m = Fg / g

Wzór m = Fg / g stanowi istotne narzędzie do obliczania masy obiektów na podstawie siły ciężkiej (Fg) oraz przyspieszenia grawitacyjnego (g). W tej formule:

• m oznacza masę, którą zamierzamy określić,
• Fg to siła ciężkości działająca na ciało w polu grawitacyjnym, mierzona w niutonach,
• g to przyspieszenie grawitacyjne, które na Ziemi wynosi około 9,81 m/s².

Ten wzór umożliwia łatwe przeliczenie ciężaru obiektu na masę, co ma kluczowe znaczenie w zastosowaniach takich jak wagi czy siłomierze. Na przykład, gdy znamy siłę ciężkości działającą na dany przedmiot, wystarczy podzielić tę wartość przez g, aby uzyskać masę.

Co więcej, równanie m = Fg / g znajduje szerokie zastosowanie w fizyce oraz inżynierii. Dzięki niemu możliwe są dokładne obliczenia w różnych dziedzinach nauki i techniki.

Jak masa, objętość i gęstość są ze sobą powiązane?

Masa, objętość i gęstość to pojęcia, które są ze sobą ściśle związane poprzez podstawowy wzór: m = d * V. W tym równaniu m oznacza masę, d gęstość, a V objętość, która stanowi miarę przestrzeni zajmowanej przez dany obiekt. W ten sposób możemy lepiej zrozumieć, jak materia jest rozmieszczona w trzech wymiarach. Gęstość ilustruje związek między masą a objętością, wskazując, ile masy znajduje się w jednostce objętości.

Gdy posiadamy dwie z tych trzech wartości, z łatwością obliczamy trzecią. Na przykład:

• mając gęstość danego materiału oraz jego objętość,
• możemy zastosować wzór m = d * V, aby obliczyć masę.

Takie podejście ułatwia inżynierom i naukowcom badanie właściwości materiałów oraz ich zachowania w różnych sytuacjach.

W dziedzinach inżynierii i fizyki, rozumienie interakcji między masą, objętością i gęstością jest niezwykle istotne. To kluczowy element przy projektowaniu oraz ocenianiu fizycznych właściwości materiałów. Przykłady zastosowań tej wiedzy obejmują wszelkiego rodzaju obliczenia w:

• budownictwie,
• inżynierii mechanicznej,
• naukach przyrodniczych.

Dzięki znajomości tych związków można skutecznie zarządzać materiałami w różnych branżach.

Definicja objętości i gęstości

Objętość to istotny czynnik fizyczny, który definiuje przestrzeń, jaką zajmuje ciało lub substancja. Mierzymy ją w różnych jednostkach, na przykład w litrach (L) czy metrach sześciennych (m³). Gęstość natomiast to relacja masy do objętości, co można ująć w prostym wzorze: d = m / V, gdzie d oznacza gęstość, m to masa, a V to objętość.

Gęstość odgrywa kluczową rolę w charakterystyce materiałów. Dzięki temu wskaźnikowi możemy ocenić, jak zwarty jest dany obiekt. Na przykład:

• gęstość wody wynosi 1 g/cm³,
• 1 cm³ wody waży dokładnie 1 gram,
• gęstości różnych substancji mogą się znacząco różnić,
• ołów jest o wiele gęstszy od wody,
• ołów łatwo opada na dno.

Zarówno objętość, jak i gęstość stanowią istotne elementy w obliczeniach masy. Umożliwiają one przejrzyste przejście między masą a objętością, co jest niezwykle pomocne. Dzięki temu naukowcy oraz inżynierowie mogą szybko oceniać właściwości fizyczne różnych substancji i przeprowadzać analizy, oparte na tych fundamentalnych wielkościach.

Przekształcenia wzoru na masę

Przekształcenia wzoru na masę są niezwykle ważne, aby lepiej zrozumieć, jak masa, objętość i gęstość współdziałają ze sobą. Podstawowy wzór, który mamy na myśli, to m = d * V. Można go modyfikować, co prowadzi do uzyskania formuł dla objętości i gęstości.

Pozwól, że przedstawię te przekształcenia:

1. Objętość: V = m / d
2. Gęstość: d = m / V

Te przekształcenia umożliwiają obliczanie objętości obiektu, gdy znamy jego masę oraz gęstość. Z kolei, dysponując masą i objętością, możemy wyznaczyć gęstość.

Te relacje tworzą fundamenty w dziedzinie fizyki, a ich zastosowanie jest szerokie. Umożliwiają one przeprowadzanie różnorodnych obliczeń dotyczących substancji oraz ich właściwości. Dodatkowo, są nieocenione w analizie parametrów fizycznych, co znajduje zastosowanie w wielu dziedzinach inżynieryjnych i naukowych.

Do czego służy masa jako wielkość fizyczna?

Masa stanowi istotny element w dziedzinie fizyki, ponieważ pozwala nam zrozumieć, jaką ilość materii zawierają różne obiekty oraz jak się poruszają i oddziałują ze sobą. Można ją klasyfikować na dwa główne typy: masę bezwładną oraz masę grawitacyjną.

• Masa bezwładna odnosi się do oporu, który obiekt stawia wobec zmian swojego ruchu,
• Masa grawitacyjna dotyczy sił przyciągających między ciałami,
• zrozumienie masy grawitacyjnej jest niezbędne do stosowania prawa powszechnego ciążenia,
• umożliwia prognozowanie ruchu planet oraz innych obiektów znajdujących się w przestrzeni,
• ma kluczowe znaczenie w definiowaniu różnych zjawisk fizycznych, takich jak energia kinetyczna czy potencjalna.

Te pojęcia są ważne zarówno w klasycznej fizyce, jak i w teorii względności. Dodatkowo, w fizyce współczesnej masa często odnosi się do masy relatywistycznej. To zagadnienie jest kluczowe dla zrozumienia procesów zachodzących przy prędkościach zbliżonych do prędkości światła oraz w badaniach dotyczących cząstek elementarnych i ich interakcji.

Masa ma również szereg praktycznych zastosowań. Umożliwia na przykład wyważanie obiektów, a także obliczanie sił w różnych dynamicznych systemach. W technologii precyzyjne pomiary masy są niezwykle ważne dla zapewnienia bezpieczeństwa oraz efektywności w różnych dziedzinach.

Masa bezwładna i oddziaływanie grawitacyjne

Masa bezwładna oraz grawitacyjna to kluczowe zagadnienia w świecie fizyki, dotyczące reakcji ciał na działające na nie siły. Masa bezwładna informuje nas o tym, jak bardzo ciało sprzeciwia się zmianom swojego ruchu. Jest to fundament drugiej zasady dynamiki Newtona, sformułowanej jako F = m * a. Oznacza to, że im większa masa bezwładna, tym silniejszy opór wobec przyspieszania lub hamowania. Na przykład, samochód ważący jedną tonę wymaga znacznie większej siły, aby zacząć się poruszać w porównaniu do roweru, który waży jedynie 10 kilogramów.

Z drugiej strony, masa grawitacyjna wyjaśnia, jak obiekty wchodzą w interakcję z siłą grawitacyjną. Prawo powszechnego ciążenia określa, że każde dwa ciała przyciągają się nawzajem siłą, której wartość zależy od iloczynu ich mas oraz odwrotnie proporcjonalne do kwadratu odległości między nimi. Doskonałym tego przykładem jest Ziemia, która przyciąga wszelkie obiekty znajdujące się w jej pobliżu, manifestując w ten sposób działanie siły grawitacyjnej.

Nie można również pominąć zasady równoważności mas bezwładnej i grawitacyjnej, która sugeruje, że te dwa rodzaje mas są w eksperymentach nieodróżnialne. Są one ze sobą ściśle powiązane i wpływają na dynamikę ruchu ciał w polu grawitacyjnym. Ta zależność ma ogromne znaczenie w ramach teorii względności Einsteina, która zmienia nasze postrzeganie grawitacji. W rzeczywistości opisuje ją jako zakrzywienie czasoprzestrzeni, będące wynikiem obecności masy.

Zastosowanie masy w dynamice Newtona

Masa bezwładna to niezwykle ważny aspekt w dynamice, zgodnej z zasadami Newtona. Jest to istotny parametr, który ma wpływ na ruch różnych obiektów. Zgodnie z drugą zasadą dynamiki, przyspieszenie obiektu (a) jest wprost proporcjonalne do siły (F), która działa na ten obiekt, a jednocześnie odwrotnie proporcjonalne do jego masy (m). Można to sprowadzić do prostego wzoru: F = m * a. Zrozumienie masy pozwala przewidywać, w jaki sposób różnorodne siły wpływają na ruch zarówno prostoliniowy, jak i obrotowy ciał.

W praktyce, znajomość masy jest niezwykle wartościowa dla inżynierów i fizyków, którzy wykorzystują ją w swoich obliczeniach dotyczących sił niezbędnych do przemieszczenia obiektów. Przykłady zastosowań masy obejmują:

• zrozumienie masy ładunku w logistyce, co jest kluczowe do określenia siły potrzebnej do jego przyspieszenia,
• wpływ masy na moment bezwładności w ruchu obrotowym, co determinuje łatwość lub trudność obrotu obiektów,
• ajednakowe wykorzystanie w różnych dziedzinach inżynierii i nauki.

Zatem masa bezwładna nie tylko ma znaczenie teoretyczne, ale również praktyczne. Stanowi fundament do analizy zjawisk związanych z ruchem oraz siłami oddziałującymi na różne obiekty w naszym otoczeniu.

Jakie są jednostki masy i jak je przeliczać?

Kilogram (kg) stanowi podstawową jednostkę masy w systemie SI, będąc kluczowym punktem odniesienia w różnych kontekstach. Obok niego ważnymi jednostkami są również gram (g) oraz tona (t). Dla lepszego zrozumienia:

• 1 kilogram to równowartość 1000 gramów,
• 1 tona to 1000 kilogramów.

Te informacje odgrywają istotną rolę w naukach przyrodniczych i technologii, ponieważ umożliwiają precyzyjne przedstawianie oraz interpretację danych dotyczących masy.

Konwersje masy są nie tylko przydatne w laboratoriach, lecz także w naszym codziennym życiu. Często podczas gotowania czy robienia zakupów musimy dostosowywać jednostki. Zrozumienie tych przeliczeń zdecydowanie ułatwia korzystanie z wag oraz analizę wyników pomiarów. Warto także zaznaczyć, że precyzyjność w nauce jest niezwykle ważna, co odnosi się również do stosowania odpowiednich jednostek masy.

Jednostka SI: kilogram

Kilogram to podstawowa jednostka masy w układzie SI, która odgrywa nieocenioną rolę zarówno w nauce, jak i w codziennym życiu. Został zdefiniowany na podstawie stałych fizycznych i stanowi globalny standard w pomiarach masy. Dzięki temu możemy precyzyjnie określić masę różnych obiektów, niezależnie od ich charakterystyki czy zastosowania.

W praktyce, kilogram jest niezwykle przydatny do przeliczania innych jednostek masy, w tym:

• jeden kilogram odpowiada tysiącu gramów,
• jedna tona to także tysiąc kilogramów,
• wszechstronność jednostki sprawia, że jest łatwo wykorzystywana w wielu dziedzinach.

Wprowadzenie kilograma jako jednostki SI miało na celu ujednolicenie pomiarów masy na całym globie, co z kolei przyczyniło się do postępu w nauce i technologii. Ponadto, kilogram stanowi podstawę wielu teorii oraz obliczeń w dziedzinie fizyki, co czyni go kluczowym elementem w zrozumieniu świata wokół nas.

Przeliczanie jednostek masy: kilogram, gram, tona

Przeliczanie jednostek masy odgrywa kluczową rolę w handlu, nauce i przemyśle. Aby lepiej to zrozumieć, warto zapoznać się z podstawowymi relacjami między kilogramami, gramami i tonami.

• 1 kilogram to 1000 gramów,
• 5 kilogramów to 5000 gramów,
• 1 tona to 1000 kilogramów,
• 2 tony to 2000 kilogramów,
• tony są powszechnie wykorzystywaną jednostką w transporcie.

Znajomość tych przeliczeń jest niezbędna w logistyce. Chociaż przeliczanie jednostek masy jest stosunkowo proste, stanowi fundament dla precyzyjnych obliczeń. Ułatwia to nie tylko wystawianie faktur, ale także obliczanie kosztów transportu i prowadzenie badań naukowych. W dziedzinie nauki dokładne pomiary są kluczowe dla uzyskania wiarygodnych wyników. Z tego powodu umiejętność szybkiego przeliczania masy między kilogramami, gramami a tonami jest niezwykle praktyczna w codziennym życiu.

Jak mierzyć masę? Metody i narzędzia

Pomiar masy można realizować na wiele sposobów. Najczęściej korzystamy z wag, które oceniasz siłę ciężkości działającą na dany obiekt. Zasada ich funkcjonowania opiera się na przeliczeniu tej siły na masę, uwzględniając przy tym przyspieszenie grawitacyjne.

Siłomierze stanowią kolejne praktyczne narzędzie do pomiaru masy. Działają na zasadzie pomiaru siły, jaką obiekt wywiera na podłoże, wyrażając ją w niutonach. Również dynamometry służą do mierzenia siły, chociaż często wykorzystuje się je w różnych kontekstach, na przykład przy pomiarze obciążeń mechanicznych.

Aby uzyskane dane były precyzyjne, niezwykle istotne jest odpowiednie kalibrowanie urządzeń pomiarowych. Warto również pamiętać, że różne warunki grawitacyjne mogą prowadzić do zróżnicowanych wyników pomiarów. To zróżnicowanie ma szczególne znaczenie, gdy eksperymenty odbywają się w różnych lokalizacjach.

Siłomierz, dynamometr i inne urządzenia

Siłomierz i dynamometr to kluczowe urządzenia stosowane do pomiaru siły, w tym także siły ciężkości działającej na różnorodne obiekty. Siłomierz, na przykład waga sprężynowa, mierzy tę siłę w niutonach, co pozwala na określenie masy obiektu na podstawie jego ciężaru. Tego rodzaju pomiary są niezwykle istotne w wielu dziedzinach, takich jak nauka i przemysł. Wagi zarówno mechaniczne, jak i elektroniczne przekształcają siłę ciężkości na masę, uwzględniając lokalne przyspieszenie grawitacyjne.

Kiedy korzystamy z siłomierza do pomiaru masy, otrzymujemy precyzyjne informacje o badanych obiektach. W laboratoriach, te narzędzia odgrywają kluczową rolę w dokładnych badaniach:

• fizycznych,
• chemicznych,
• biologicznych.

Ponadto, dynamometry znajdują szerokie zastosowanie w inżynierii, gdzie analizują właściwości materiałów oraz siły wpływające na różne konstrukcje.

Należy zaznaczyć, że większość nowoczesnych wag elektronicznych opiera się na pomiarze siły ciężkości. Dzięki temu proces ustalania masy obiektu staje się szybki i precyzyjny. Takie urządzenia są bardzo efektywne i znajdują zastosowanie w naszym codziennym życiu, zarówno w kuchni, jak i w przemyśle.

Jaka jest różnica między masą a ciężarem?

Masa i ciężar to dwa odrębne pojęcia, które odgrywają istotną rolę w fizyce. Masa określa ilość materii w danym obiekcie. To wartość skalarna, czyli niezmienna, niezależnie od tego, gdzie się znajdujemy. Czy jesteśmy na Ziemi, czy w przestrzeni kosmicznej, masa obiektu pozostaje taka sama. Zazwyczaj wyrażamy ją w kilogramach (kg) lub gramach (g).

Ciężar to siła, z jaką masa oddziałuje na pole grawitacyjne. Możemy go obliczyć, stosując wzór: F_g = m · g. W tej formule F_g oznacza siłę ciężkości, m to masa, a g to przyspieszenie grawitacyjne, które na naszej planecie wynosi około 9,81 m/s². Wartość ciężaru zmienia się w zależności od lokalizacji; na przykład na Księżycu ciężar obiektu to tylko 1/6 tego, co waży na Ziemi.

W skrócie, masa pozostaje stała w różnych warunkach, natomiast ciężar zmienia się w zależności od działania grawitacji. Zrozumienie różnicy między tymi pojęciami jest niezwykle istotne, ponieważ umożliwia lepszą analizę zjawisk fizycznych oraz dokładniejsze pomiary.

Masa a siła ciężkości

Masa to ilość materii obecnej w danym obiekcie. Jest to wielkość stała, która nie zmienia się pod wpływem zmiennych warunków zewnętrznych. Z kolei siła ciężkości, oznaczana symbolem Fg, oddziałuje na masę obiektu na skutek działania pola grawitacyjnego. Możemy ją obliczyć korzystając ze wzoru Fg = m * g, gdzie g to przyspieszenie grawitacyjne. Na naszej planecie wynosi ono około 9,81 m/s².

Warto zrozumieć różnicę między masą a ciężarem. Masa obiektu jest niezmienna, natomiast siła ciężkości może różnić się w zależności od miejsca, w którym się znajdujemy. Na przykład, na Księżycu przyspieszenie grawitacyjne wynosi tylko około 1,62 m/s², co oznacza, że siła ciężkości tam jest znacznie mniejsza niż na Ziemi.

Możliwe jest zmierzenie siły ciężkości, co pozwala nam pośrednio oszacować masę obiektu. Kiedy korzystamy z siłomierza, określamy, jaką siłę grawitacja wywiera na dany przedmiot. Ta informacja, w połączeniu z wartością g, umożliwia nam z łatwością obliczenie masy. Na przykład, jeśli siłomierz wskazuje wartość 20 N na Ziemi, masa obiektu wynosi około 2,04 kg (20 N / 9,81 m/s²).

Warto również zauważyć, że masa odgrywa istotną rolę w dynamice obiektów w fizyce. Obiekty o większej masie potrzebują większych sił, aby uzyskać tę samą akcelerację. To jest zgodne z drugą zasadą dynamiki Newtona ( F = m * a ).

Wpływ przyspieszenia grawitacyjnego

Wpływ przyspieszenia grawitacyjnego to fundamentalne zagadnienie w fizyce, które odgrywa kluczową rolę w zrozumieniu działania sił na obiekty. Na Ziemi jego wartość wynosi około 9,81 m/s², co pozwala nam określić, jak silnie grawitacja oddziałuje na różne ciała. Interesujące jest to, że obiekty o identycznej masie mogą różnić się ciężarem w zależności od miejsca, ponieważ wartość przyspieszenia grawitacyjnego nie jest stała. Na przykład, na Księżycu siła ta jest znacznie mniejsza.

Choć masa obiektu pozostaje niezmienna, to jednak siła ciężkości, której wartość wyliczamy za pomocą wzoru Fg = m * g, zmienia się w zależności od g, co ma swoje praktyczne zastosowania. Różnice w ciężarze wpływają na sposób, w jaki posługujemy się wagami oraz siłomierzami, które muszą być dostosowane do lokalnego przyspieszenia grawitacyjnego, aby zapewnić dokładne pomiary.

Zrozumienie związku między masą a siłą ciężkości jest niezwykle ważne w wielu dziedzinach naukowych, ponieważ umożliwia precyzyjne obliczenia oraz lepszą analizę ruchu obiektów w polu grawitacyjnym.

Jak obliczyć masę ciała człowieka?

Obliczanie masy ciała człowieka opiera się na wskaźniku masy ciała, znanym jako BMI. To narzędzie odgrywa istotną rolę w ocenie kondycji fizycznej oraz stanu zdrowia. Aby obliczyć BMI, można skorzystać z prostego wzoru:

\[ \text{BMI} = \frac{\text{masa (kg)}}{\text{wzrost (m)}^2} \]

Innymi słowy, wystarczy podzielić masę ciała wyrażoną w kilogramach przez kwadrat wzrostu w metrach. Weźmy na przykład osobę ważącą 70 kg i mającą 1,75 m wzrostu. Jej BMI wyniesie:

\[ \text{BMI} = \frac{70}{(1,75)^2} \approx 22,86 \]

Wartości BMI mają swoje specyficzne znaczenie zdrowotne, które można określić w następujący sposób:

• BMI poniżej 18,5 – niedowaga,
• BMI 18,5 – 24,9 – waga prawidłowa,
• BMI 25 – 29,9 – nadwaga,
• BMI powyżej 30 – otyłość.

Oprócz wskaźnika BMI istnieje szereg innych wzorów, takich jak te zaproponowane przez Broca, Lorentza, Pottona i Robinsona. Te alternatywne metody również pomagają w oszacowaniu idealnej masy ciała, z uwzględnieniem takich elementów jak płeć i wzrost.

Przykładowo, wzór Broca na obliczanie idealnej masy ciała prezentuje się następująco:

• Dla mężczyzn: idealna masa (kg) = wzrost (cm) – 100,
• Dla kobiet: idealna masa (kg) = wzrost (cm) – 105.

Każdy z tych wzorów oferuje cenne wskazówki, które mogą być dostosowane do osobistych potrzeb. Zrozumienie metod obliczania masy ciała jest kluczowe dla śledzenia swojego zdrowia. Dzięki temu można podejmować świadome decyzje dotyczące stylu życia.

Wzór BMI i interpretacja wskaźnika masy ciała

Wzór na wskaźnik masy ciała, czyli BMI, opiera się na prostej formule: BMI = masa (kg) / (wzrost (m))². Na przykład, jeśli ktoś ma 70 kg wagi oraz 1,75 m wzrostu, proces obliczania BMI wygląda tak: 70 / (1,75)² = 22,86.

Wartości BMI można interpretować w sposób następujący:

• wartość poniżej 18,5 oznacza niedowagę,
• zakres od 18,5 do 24,9 to norma,
• wyniki od 25 do 29,9 wskazują na nadwagę,
• wartość 30 lub wyższa sugeruje otyłość.

Niemniej jednak, wskaźnik BMI ma pewne ograniczenia. Nie uwzględnia rozkładu masy ciała, co może prowadzić do mylnych wniosków, szczególnie w przypadku sportowców lub osób o dużej masie mięśniowej. Ponadto, BMI nie bierze pod uwagę takich czynników jak wiek, płeć czy rasa, które mogą wpływać na jego wyniki. Dlatego też, BMI powinno być postrzegane głównie jako narzędzie wstępnej oceny zdrowia, a nie jedyny wskaźnik ogólnego stanu zdrowia.

Alternatywne wzory: Broca, Lorentza, Pottona, Robinsona

Alternatywne metody oceny masy ciała są cennymi narzędziami w dziedzinie medycyny oraz zdrowia. Wzory Broca, Lorentza, Pottona i Robinsona pomagają ustalić optymalną wagę, uwzględniając różne aspekty, takie jak wzrost czy płeć.

Najbardziej podstawowy jest wzór Broca. Aby go zastosować, wystarczy od wysokości w centymetrach odjąć 100. Na przykład, osoba mierząca 180 cm powinna ważyć około 80 kg, mając na uwadze, że rezultaty mogą być modyfikowane w zależności od typu ciała.

Wzór Lorentza jest nieco bardziej złożony. Dostarcza różnych wyników w zależności od płci. Dla mężczyzn obliczenia opierają się na wzroście minus 100 oraz dodaniu wartości specyficznych, natomiast u kobiet od tej liczby odejmuje się dodatkowe 5-10 kg.

Wzór Pottona, podobnie jak Lorentza, także uwzględnia zarówno wzrost, jak i płeć, ale wprowadza bardziej szczegółowe informacje o indywidualnych cechach sylwetki. Dzięki temu można przyjąć bardziej spersonalizowane podejście do określenia właściwej masy ciała.

Z kolei wzór Robinsona jest znany ze swojej prostoty i dokładności. Zawiera podobną formułę, gdzie od wzrostu odejmuje się 100, a następnie dokonuje korekt w zależności od płci.

Te różne wzory są niezwykle istotne w kontekście oceny masy ciała. Dostarcza to rozmaitych metod na oszacowanie idealnej wagi, co ma kluczowe znaczenie dla zdrowia oraz medycyny.

Jakie czynniki wpływają na prawidłową masę ciała?

Prawidłowa masa ciała jest wynikiem kilku kluczowych czynników wpływających na nasze zdrowie i samopoczucie. Wśród najważniejszych z nich można wymienić:

• wiek,
• płeć,
• rasę,
• rozmieszczenie masy ciała.

Z wiekiem nasz metabolizm często zwalnia, co może skutkować trudnościami w utrzymaniu zdrowej wagi. Dodatkowo, różnice płciowe mają znaczenie; u kobiet zazwyczaj obserwuje się wyższy poziom
tkanki tłuszczowej niż u mężczyzn.

Rozmieszczenie masy ciała, czyli proporcje tkanki tłuszczowej do masy mięśniowej, jest istotnym elementem oceny prawidłowej wagi. Osoby, które mają więcej mięśni, częściej osiągają wyższy wskaźnik podstawowej przemiany materii (BMR), co z kolei sprzyja efektywniejszemu spalaniu kalorii.

Nie można zapominać o nawykach żywieniowych i ogólnym sposobie odżywiania, które odgrywają równie ważną rolę. Zrównoważona dieta, kontrola porcji oraz ograniczenie spożycia przetworzonej żywności mogą zdecydowanie wpłynąć na utrzymanie zdrowej masy ciała. Dodatkowo, regularna aktywność fizyczna jest kluczowa; sprzyja nie tylko prawidłowemu metabolizmowi, ale także poprawia kondycję układu sercowo-naczyniowego.

Regularne podejmowanie działań w celu monitorowania postępów, takich jak:

• regularne ważenie,
• analiza składu ciała,
• tworzenie planu zdrowotnego,
• uwzględnianie wszystkich aspektów,
• utrzymanie aktywności fizycznej.

dostarcza cennych informacji o naszym stanie zdrowia. Stworzenie planu zdrowotnego, który uwzględnia te wszystkie aspekty, może znacznie ułatwić osiągnięcie i utrzymanie prawidłowej masy ciała oraz ogólnej kondycji fizycznej.

Rola wieku, płci i rozkładu masy

Wiek, płeć oraz rozkład masy ciała to kluczowe elementy mające znaczący wpływ na nasze zdrowie oraz na to, jaka masa ciała jest dla nas właściwa. W miarę upływu lat nasz metabolizm ulega zmianom, co może prowadzić do spadku masy mięśniowej i zwiększenia ilości tkanki tłuszczowej. Dlatego starsze osoby mogą mieć inne potrzeby dotyczące wagi niż ich młodsze odpowiedniki.

Różnice płci także odgrywają istotną rolę w tym kontekście. Mężczyźni zazwyczaj mają więcej mięśni i mniej tkanki tłuszczowej w porównaniu do kobiet. Stąd też zdrowe normy masy ciała różnią się dla każdej z płci.

Nie można również zignorować rozmieszczenia masy ciała, które ma ogromne znaczenie dla naszego zdrowia. Osoby z nadmiernym tłuszczem w okolicach brzuszka są bardziej narażone na schorzenia takie jak:

• choroby sercowo-naczyniowe,
• cukrzyca,
• problemy z układem pokarmowym.

Dlatego kompleksowa ocena kondycji fizycznej powinna brać pod uwagę wszystkie te aspekty. Wiedza na temat wieku, płci oraz rozkładu masy ciała jest zatem niezbędna w diagnostyce oraz w planowaniu strategii zdrowotnych i żywieniowych.

Znaczenie zdrowej diety i aktywności fizycznej

Zdrowa dieta i aktywność fizyczna to kluczowe elementy, które pozwalają utrzymać prawidłową wagę ciała, a tym samym przyczyniają się do ogólnego zdrowia i samopoczucia. Zrównoważone odżywianie, obfitujące w niezbędne składniki, wspiera organizm w codziennym funkcjonowaniu. Ważne jest także kontrolowanie wielkości porcji, aby uniknąć spożywania nadmiaru kalorii, co w dłuższej perspektywie może prowadzić do problemów z wagą.

Regularne treningi przyspieszają metabolizm, co sprzyja efektywnemu spalaniu kalorii. Oprócz tego, ćwiczenia wzmacniają mięśnie i zwiększają wytrzymałość, dzięki czemu poprawia się ogólna kondycja fizyczna. Monitorowanie postępów, na przykład przez analizę masy ciała czy notowanie aktywności fizycznej, ułatwia dostrzeganie zdrowych nawyków i ewentualnych potrzebnych zmian.

Niezwykle istotne są również nawyki związane z myśleniem o zdrowym żywieniu i ruchu. Ustanowienie realistycznych celów oraz regularne ich przeglądanie mogą znacząco wpłynąć na długoterminowy sukces w utrzymaniu prawidłowej wagi. Dlatego też dbanie o odpowiednią dietę oraz aktywność fizyczną stanowi fundament dla dobrego zdrowia i samopoczucia.

Jakie jest znaczenie masy w fizyce współczesnej?

Masa odgrywa niezwykle istotną rolę w nowoczesnej fizyce, zwłaszcza w ramach teorii względności oraz badań nad cząstkami elementarnymi. Masa spoczynkowa, która jest stała w różnych układach odniesienia, stanowi podstawę tej teorii. Według odkryć Einsteina, masa i energia są ze sobą ściśle związane, co zostało zilustrowane słynnym równaniem E=mc². Warto również zauważyć, że masa relatywistyczna zmienia się w zależności od prędkości, z jaką porusza się obiekt. Kiedy obiekt zyskuje prędkość, jego masa zwiększa się z perspektywy stacjonarnego obserwatora.

W kontekście cząstek elementarnych, pole Higgsa ma kluczowe znaczenie, ponieważ nadaje masę tym cząstkom. To odkrycie potwierdza hipotezy dotyczące mechanizmu, który wyjaśnia zróżnicowanie mas w naturze. Interakcja pola Higgsa z cząstkami sprawia, że te zyskują swoją masę, co jest niezbędne dla pełniejszego zrozumienia struktury materii.

Ponadto masa odgrywa istotną rolę w reakcjach jądrowych. W takich procesach jak fuzja czy rozpad, masa przekształca się w energię, co ilustruje wymianę między tymi dwiema wielkościami. Dlatego masa w nowoczesnej fizyce to nie tylko wyraz ilości materii, ale także kluczowy aspekt w zachodzących procesach energetycznych oraz fundamentalnych teoriach.

Masa relatywistyczna i teoria względności

Masa relatywistyczna to kluczowe zagadnienie w teorii względności, które mówi o tym, jak masa obiektu zmienia się, gdy jego prędkość zbliża się do prędkości światła w danym układzie odniesienia. Kiedy obiekt przyspiesza, możemy zaobserwować, że jego masa relatywistyczna wzrasta. To zjawisko doskonale ilustruje, jak prędkość wpływa na fizyczne właściwości ciał. W odróżnieniu od tego, masa spoczynkowa pozostaje niezmienna, niezależnie od tego, czy obiekt jest w ruchu, czy stoi w miejscu.

Albert Einstein w swojej „Teorii względności” zaprezentował istotne zależności między masą a energią, opierając się na słynnym równaniu E=mc². To równanie ukazuje, jak ściśle związane są ze sobą masa i energia, co jest kluczowe do zrozumienia procesów zachodzących w fizyce na poziomie subatomowym. W przypadku cząstek elementarnych, masa relatywistyczna ma znaczenie w kontekście ich interakcji z polem Higgsa oraz wpływa na zjawiska związane z przemianami jądrowymi.

W rezultacie masa relatywistyczna nie tylko rozszerza nasze horyzonty na temat samej masy, ale także zmienia nasze postrzeganie czasu, przestrzeni oraz fundamenty, na których oparty jest cały wszechświat.

Cząstki elementarne i pole Higgsa

Cząstki elementarne zyskują swoją masę dzięki interakcji z polem Higgsa, które zostało odkryte w 2012 roku w CERN. To pole odgrywa fundamentalną rolę w Modelu Standardowym fizyki cząstek, działając na zasadzie spontanicznego łamania symetrii.

Mechanizm ten pozwala takim cząstkom jak:

• kwarki,
• leptony,
• na oddziaływanie z polem Higgsa,
• co skutkuje przyznawaniem im masy.

To zjawisko tłumaczy, dlaczego niektóre z nich mają masę, podczas gdy inne, jak fotony, pozostają bezmasowe. Bez istnienia tego pola, cząstki poruszałyby się jedynie z prędkością światła, co uniemożliwiłoby tworzenie atomów i, w konsekwencji, materii, która nas otacza.

Zrozumienie tego mechanizmu jest kluczowe dla badań nad strukturą wszechświata oraz siłami rządzącymi fizyką.

Przemiany i reakcje jądrowe a masa

Przemiany i reakcje jądrowe pełnią kluczową rolę w odkrywaniu tajemnic masy w fizyce. W trakcie tych procesów masa ulega zmianie, co jest ściśle związane z energią, która jest uwalniana lub absorbowana. To zjawisko doskonale ilustruje słynne równanie Einsteina: E=mc². W skrócie, masa i energia są nierozerwalnie ze sobą powiązane i mogą przekształcać się jedna w drugą.

Na przykład, podczas fuzji jądrowej, która ma miejsce w sercach gwiazd:

• masa końcowych produktów jest niższa niż masa zareagujących jąder,
• różnica ta, znana jako defekt masy, prowadzi do wydobycia ogromnych ilości energii,
• to sprawia, że rodzi się światło i ciepło, które dociera do naszej planety.

Z drugiej strony, w reakcjach rozszczepienia jądrowego, typowych dla reaktorów atomowych:

• niewielkie ilości masy przekształcają się w znaczne ilości energii,
• ten proces stanowczo dowodzi, że masa jest istotnym źródłem energii w tych operacjach.

Opanowanie tych zjawisk stanowi fundament dla działań związanych z energetyką jądrową oraz kosmologią. Właściwie, większość materii we wszechświecie zrodziła się z reakcji jądrowych.

Obserwacja tych procesów ma również kluczowe znaczenie w badaniach nad cząstkami elementarnymi oraz polem Higgsa, gdzie masa pełni fundamentalną rolę w naszym pojmowaniu struktury wszechświata.