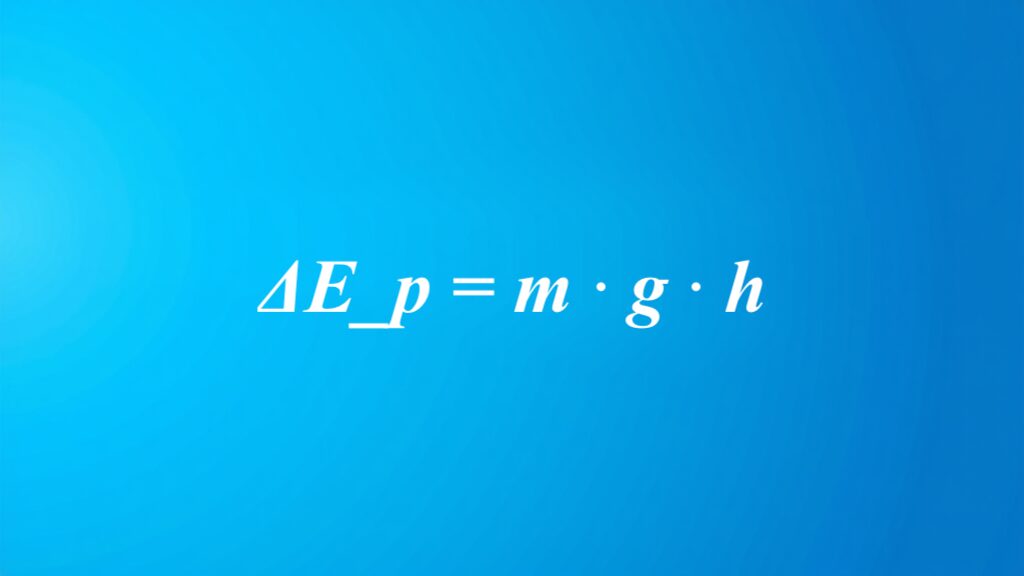Wzór na energię potencjalną

Energia potencjalna to forma energii zmagazynowanej w obiekcie, ściśle związana z jego położeniem lub stanem w obrębie pola sił, jak na przykład grawitacyjnego czy sprężystego. Jest to rodzaj energii mechanicznej, która czeka na swoje uwolnienie i może przekształcić się w inne formy, takie jak energia kinetyczna, gdy obiekt zmienia swoje położenie lub stan.

w fizyce energia potencjalna odgrywa niezwykle istotną rolę. Reprezentuje zdolność systemu do wykonania pracy w przyszłości, dzięki dotychczas nagromadzonej energii. Możemy tu wyróżnić różne typy energii potencjalnej:

energia grawitacyjna,
energia sprężysta,
energia elektryczna.

Co więcej, energia potencjalna pojawia się w wielu kontekstach, co sprawia, że jest kluczowym zagadnieniem w dziedzinie nauk przyrodniczych.

Jakie są rodzaje energii potencjalnej?

Energia potencjalna występuje w różnych wariantach, które są uzależnione od działających sił oraz pól fizycznych. Do najważniejszych typów energii potencjalnej zaliczamy:

energię grawitacyjną,
energię sprężystą,
energię elektryczną.

Energia potencjalna grawitacyjna pojawia się, gdy obiekt znajduje się w polu grawitacyjnym. Jej wartość jest uwarunkowana masą przedmiotu oraz jego wysokością w odniesieniu do wybranego poziomu. Na przykład, gdy podnosimy coś na określoną wysokość, obiekt zyskuje potencjalną energię grawitacyjną.

Energia potencjalna sprężysta odnosi się do materiałów zdolnych do odkształcania się, takich jak sprężyny i gumki. Ta forma energii jest ściśle powiązana z charakterystykami materiałów oraz stopniem ich deformacji.

Potencjalna energia elektryczna odnosi się do ładunków znajdujących się w polu elektrycznym. Jej ilość zależy od wielkości ładunku oraz różnicy potencjałów. Dobrym przykładem jest kondensator, który, gdy jest naładowany, gromadzi energię potencjalną elektryczną.

Nie możemy zapomnieć o innych rodzajach energii potencjalnej, do których należy:

energia chemiczna,
energia jądrowa,
energia magnetyczna.

Zrozumienie tych różnych form energii potencjalnej ma kluczowe znaczenie w dziedzinach takich jak fizyka i inżynieria. Poznanie ich właściwości pozwala na ich efektywne wykorzystanie w praktycznych zastosowaniach.

Energia potencjalna grawitacyjna

Energia potencjalna grawitacyjna to ta forma energii, którą posiada obiekt o masie m, kiedy znajduje się na wysokości h względem ustalonego punktu odniesienia w polu grawitacyjnym Ziemi lub innego ciała niebieskiego. Jej wartość uzależniona jest od trzech kluczowych elementów:

masy obiektu,
wysokości względem poziomu odniesienia,
przyspieszenia grawitacyjnego g, które wynosi około 9,81 m/s².

Ta energia odpowiada pracy wykonanej przez siłę ciężkości podczas podnoszenia obiektu na daną wysokość.

Możemy wyrazić energię potencjalną grawitacyjną za pomocą wzoru: Ep = m · g · h, gdzie:

Ep oznacza energię potencjalną,
m to masa,
g to przyspieszenie ziemskie,
h to wspomniana wysokość.

Ta wartość jest niezbędna do analizy ruchu obiektów w polu grawitacyjnym. Na przykład, umożliwia obliczenie prędkości ucieczki, czyli minimalnej prędkości, jaką musi osiągnąć obiekt, aby opuścić pole grawitacyjne konkretnej planety.

Zarówno potencjał pola grawitacyjnego, jak i jego natężenie mają wpływ na energię potencjalną. Należy również pamiętać, że wybór punktu odniesienia odgrywa kluczową rolę – energia potencjalna zawsze jest określana w stosunku do tego poziomu. Co więcej, energia potencjalna grawitacyjna znajduje zastosowanie w różnych dziedzinach, takich jak:

fizyka,
astronomia,
technika.

Zwłaszcza w kontekście analizy sił grawitacyjnych oraz ruchu obiektów.

Energia potencjalna sprężystości

Energia potencjalna sprężystości to forma energii, która gromadzi się w materiałach sprężystych, gdy doznają one odkształcenia. Można ją zaobserwować w różnych obiektach, takich jak:

rozciągnięta sprężyna,
napięty łuk,
ugięta trampolina,
gumka do mazania.

Ilość tej energii jest uzależniona od współczynnika sprężystości (k), który określa sztywność danego ciała, oraz od kwadratu przemieszczenia (x). Zjawisko to można przedstawić prostym wzorem:

Ep = 1/2 k x²

To oznacza, że energia potencjalna sprężystości odpowiada pracy, która jest konieczna, aby odkształcić dany obiekt. Warto pamiętać, że siła sprężystości działa zgodnie z prawem Hooke’a, co sprawia, że jest ona proporcjonalna do przemieszczenia.

Zainteresowane osoby mogą zauważyć, że ta energia dostarcza informacji na temat ilości energii mechanicznej, która jest zgromadzona w odkształconym obiekcie. Co więcej, kiedy odkształcenie ustępuje, energia ta może przekształcić się w inne formy, na przykład w energię kinetyczną.

Energia potencjalna elektryczna

Energia potencjalna elektryczna odnosi się do energii związanej z lokalizacją ładunku elektrycznego w określonym polu elektrycznym. W tym kontekście kluczowymi pojęciami są wartość ładunku elektrycznego (q) oraz potencjał elektryczny (V), które opisują warunki w określonym punkcie pola.

Potencjał elektryczny można rozumieć jako energię przypadającą na jednostkę ładunku. Z kolei różnica potencjałów, znana lepiej jako napięcie elektryczne, mierzy wysiłek potrzebny do przemieszczenia ładunku z jednego miejsca do drugiego. Możemy wyrazić energię potencjalną elektryczną za pomocą prostego wzoru: Ep = q · V.

Pole elektryczne występuje w dwóch głównych typach:

pole jednorodne, w którym natężenie pozostaje stałe w całym obszarze,
pole centralne, gdzie natężenie zmienia się w miarę oddalania od źródła.

Siła działająca na ładunek próbny umieszczony w polu jest określana przez natężenie tego pola, co z kolei wpływa na wartość energii potencjalnej, jaką ten ładunek może posiadać.

Od czego zależy energia potencjalna?

Energia potencjalna jest ściśle związana z właściwościami obiektów oraz polami, w których się znajdują. W kontekście energii potencjalnej grawitacyjnej wyróżniamy trzy kluczowe czynniki:

masa ciała,
wysokość, na której się ono znajduje,
intensywność pola grawitacyjnego, które wpływa na ten obiekt.

Z kolei energia potencjalna sprężystości uzależniona jest od właściwości materiału, w tym współczynnika sprężystości, a także od stopnia odkształcenia lub przemieszczenia, które zachodzi w sprężystym ciele. Natomiast energia potencjalna elektryczna związana jest z oddziaływaniem pola elektrycznego, przy czym jej wartość określają zarówno ładunki elektryczne, jak i potencjał elektryczny w danym miejscu.

Wszystkie wymienione rodzaje energii mają jeden wspólny element: punkt odniesienia. To on jest podstawą, na której opiera się pomiar energii potencjalnej. Bez takiego odniesienia trudno byłoby zrozumieć, ile energii potencjalnej posiada dany obiekt.

Masa i wysokość obiektu

Masa oraz wysokość obiektu odgrywają fundamentalną rolę w kształtowaniu wartości energii potencjalnej grawitacyjnej. Masa odnosi się do ilości materii zgromadzonej w obiekcie, z kolei wysokość to wyrażona w pionie odległość od ustalonego poziomu odniesienia, najczęściej oznaczającego powierzchnię ziemi. Aby obliczyć energię potencjalną, posługujemy się wzorem:

E_p = m · g · h.

W tej formule:

„m” reprezentuje masę,
„g” oznacza przyspieszenie ziemskie, które wynosi 9,81 m/s²,
„h” to wysokość w odniesieniu do wybranego punktu.

Kiedy zarówno masa, jak i wysokość wzrastają, energia potencjalna zyskuje na sile. To zjawisko stanowi kluczowy element analizy zjawisk związanych z polem grawitacyjnym. Dodatkowo, uwzględnienie odpowiedniego punktu odniesienia jest niezbędne do precyzyjnego określenia wartości energii potencjalnej konkretnego obiektu.

Pole grawitacyjne i siła grawitacji

Pole grawitacyjne to strefa otaczająca masę, w której siła grawitacji działa na inne obiekty, przyciągając je do siebie. Grawitacja, znana także jako siła ciężkości, oddziałuje na masę m zgodnie z równaniem F = m · g, gdzie g oznacza przyspieszenie ziemskie.

Natężenie pola grawitacyjnego wskazuje nam, jak silna jest ta siła w danym miejscu, a jego wartość ma ogromne znaczenie dla energii potencjalnej grawitacyjnej. Siły grawitacyjne, będące siłami zachowawczymi, pozwalają na dokładne obliczenie energii potencjalnej w obrębie pola grawitacyjnego.

Mówiąc o energii potencjalnej, warto zwrócić uwagę, że jest ona uzależniona od kilku elementów:

masy obiektu,
natężenia pola grawitacyjnego,
wysokości nad ustalonym punktem odniesienia.

Na przykład, im wyżej znajduje się dany obiekt, tym większą posiada energię potencjalną. Co więcej, zmiana masy obiektu będzie miała wpływ na wartość energii przypisanej do jego pozycji w polu grawitacyjnym.

Właściwości sprężyste i odkształcenie

Właściwości sprężyste materiału są określane przez współczynnik sprężystości, znany jako k. To właśnie ten parametr informuje nas, jak skutecznie dany materiał wraca do pierwotnego kształtu po przekształceniu. Odkształcenie, inaczej określane jako przemieszczenie x, to z kolei zmiana długości lub kształtu sprężystego ciała.

Prawo Hooke’a wskazuje, że siła sprężystości jest wprost proporcjonalna do poziomu odkształcenia i działa w przeciwną stronę. Energia potencjalna związana ze sprężystością można wyrazić za pomocą wzoru Ep = 1/2 k x². To oznacza, że:

im większe odkształcenie,
wyższy współczynnik sprężystości,
tym więcej energii jest gromadzone w obiekcie.

Siła sprężystości wykonuje pracę, gdy materiał się odkształca i następnie powraca do pierwotnego kształtu.

Ładunek i pole elektryczne

Ładunek elektryczny stanowi fundamentalną cechę cząstek, decydującą o ich interakcji z polem elektrycznym. To pole otacza ładunek i jest obszarem, w którym siła elektryczna oddziałuje na inne ładunki. Intensywność pola elektrycznego, określająca siłę przypadającą na jednostkowy ładunek, mierzy się w niutonach na kulomb (N/C).

Potencjał elektryczny, w skrócie związany z energią potencjalną przypadającą na jednostkę ładunku, wyraża się w woltach (V). Różnica potencjałów, znana jako napięcie elektryczne, wskazuje na pracę wymaganą do przesunięcia ładunku między dwoma punktami w obrębie pola.

Aby lepiej poznać właściwości pola elektrycznego, wprowadzamy ładunek próbny. Dzięki temu możemy badać kierunek i natężenie pola bez jego zakłócania. W jednorodnym polu elektrycznym natężenie pozostaje niezmienne w każdym miejscu. Z kolei w przypadku centralnego pola elektrycznego, wytwarzanego przez punktowy ładunek, zarówno natężenie, jak i potencjał ulegają zmianie w zależności od odległości od źródła ładunku.

Energia potencjalna elektryczna ściśle wiąże się z wartością ładunku oraz z potencjałem w określonym miejscu w polu. Innymi słowy, większy ładunek lub wyższy potencjał zwiększają energię potencjalną związanej z nim cząstki.

Jaki jest wzór na energię potencjalną?

Wzory na energię potencjalną różnią się w zależności od jej specyfiki.

Jeśli mówimy o energii potencjalnej grawitacyjnej, to odpowiednia formuła brzmi:

Ep = m · g · h.

W tym równaniu:

m oznacza masę obiektu, wyrażoną w kilogramach,
g to przyspieszenie ziemskie, wynoszące mniej więcej 9,81 m/s²,
h to wysokość obiektu względem wybranego poziomu odniesienia, mierzona w metrach.

Kiedy rozważamy energię potencjalną sprężystości, posługujemy się inną formułą:

Ep = 1/2 k x².

Tutaj:

k to współczynnik sprężystości sprężyny, wyrażany w N/m,
x to odkształcenie sprężyny, również wyrażane w metrach.

Dla energii potencjalnej elektrycznej mamy jeszcze inny wzór:

Ep = q · V.

W tym przypadku:

q reprezentuje ładunek elektryczny w kulombach,
V to potencjał elektryczny, wyrażony w woltach.

Dzięki tym równaniom możemy precyzyjnie określić ilość energii potencjalnej, która jest skumulowana w danym systemie fizycznym.

Wzór na energię potencjalną grawitacyjną: Ep = m · g · h

Wzór na energię potencjalną grawitacyjną to Ep = m · g · h. W tej formule:

m oznacza masę obiektu, wyrażoną w kilogramach,
g to przyspieszenie ziemskie, które wynosi około 9,81 m/s²,
h to wysokość, na jakiej znajduje się ciało w odniesieniu do ustalonego poziomu, mierzona w metrach.

Energia potencjalna grawitacyjna odnosi się do energii, jaką posiada obiekt dzięki swemu położeniu w polu grawitacyjnym Ziemi. Jej wartość, Ep, odpowiada pracy wykonywanej przez siłę ciężkości, gdy obiekt jest podnoszony na wysokość h.

Jednostką energii potencjalnej jest dżul (J), co można zrozumieć jako pracę wykonaną przez siłę jednego niutona, gdy przemieszcza ona obiekt na dystans jednego metra.

Przy zastosowaniu tego wzoru można łatwo obliczyć energię zgromadzoną przez dany obiekt na określonej wysokości. Tego rodzaju obliczenia są kluczowe w dziedzinie mechaniki oraz energetyki.

Wzór na energię potencjalną sprężystości: Ep = 1/2 k x²

Wzór na energię potencjalną sprężystości to Ep = 1/2 k x². W tym równaniu k reprezentuje współczynnik sprężystości, który określa, jak sztywny jest dany materiał, natomiast x odnosi się do odkształcenia, czyli przemieszczenia ciała sprężystego od jego pozycji równowagi.

Energia potencjalna sprężystości jest równoznaczna z pracą wykonaną podczas rozciągania lub ściśnięcia sprężyny. Zasada ta jest ujęta w prawie Hooke’a, które wskazuje, że siła sprężystości F jest równa -kx. Wartość energii sprężystości wyrażana jest w dżulach (J), powszechnie używanej jednostce w mechanice.

Ten wzór umożliwia obliczenie energii zgromadzonej w trakcie deformowania elementów sprężystych, co ma istotne zastosowanie w różnych obszarach techniki oraz fizyki.

Wzór na energię potencjalną elektryczną: Ep = q · V

Energia potencjalna elektryczna może być obliczona za pomocą prostego wzoru:

Ep = q · V

Gdzie q oznacza ładunek elektryczny, a V to potencjał elektryczny w określonym punkcie pola.

Potencjał elektryczny wskazuje na ilość energii potencjalnej przypadającą na jednostkowy ładunek. Z kolei różnica potencjałów, znana również jako napięcie elektryczne, odzwierciedla pracę, jaką trzeba wykonać, aby przenieść ładunek pomiędzy dwoma punktami w obszarze pola elektrycznego.

Taki wzór odgrywa kluczową rolę w dziedzinie elektrostatyki i znajduje zastosowanie w wielu obszarach inżynierii. Dzięki niemu można oszacować energię zgromadzoną przez ładunki w polu elektrycznym.

Jak obliczyć energię potencjalną?

Aby określić energię potencjalną, wykorzystaj właściwe wzory oraz odpowiednie parametry fizyczne. Istotne są trzy elementy:

masa obiektu,
jego wysokość,
wartość przyspieszenia ziemskiego.

Wzór, który za tym stoi, to Ep = m · g · h, gdzie Ep oznacza energię potencjalną, m to masa w kilogramach, g to przyspieszenie ziemskie wynoszące około 9,81 m/s², a h to wysokość w metrach.

Natomiast przy obliczaniu energii potencjalnej sprężystości, konieczne będzie uwzględnienie współczynnika sprężystości oraz odkształcenia samej sprężyny. W tym wypadku posłużysz się wzorem: Ep = 1/2 · k · x², gdzie k to współczynnik sprężystości mierzony w niutonach na metr, a x to odkształcenie sprężyny podawane w metrach.

Jeśli chodzi o energię potencjalną elektryczną, potrzebujesz informacji o ładunku elektrycznym oraz potencjale elektrycznym. Tutaj wzór wygląda następująco: Ep = q · V, gdzie q to ładunek w kulombach, a V to potencjał wyrażany w woltach.

Wszystkie obliczenia wymagają ustalenia punktu odniesienia, który definiuje poziom zerowy energii potencjalnej. Nie zapominaj, że energia potencjalna wyrażana jest w dżulach (J). Wprowadzając odpowiednie wartości do wzoru, możesz dokładnie obliczyć energię potencjalną konkretnego układu lub obiektu.

Przykłady obliczeń energii potencjalnej

Przykłady obliczeń energii potencjalnej ilustrują różnorodne zjawiska fizyczne, w których wykorzystujemy określone wzory. Oto trzy główne rodzaje energii potencjalnej:

energia potencjalna grawitacyjna: Aby obliczyć energię potencjalną grawitacyjną ciała o masie m, które zostało podniesione na wysokość h względem poziomu odniesienia, stosujemy wzór:
Ep = m · g · h
gdzie g oznacza przyspieszenie ziemskie, wynoszące około 9,81 m/s². Przykład: ciało o masie 5 kg, podniesione na 10 metrów, ma energię potencjalną wynoszącą 490,5 J,
energia potencjalna sprężystości: Obliczana jest za pomocą współczynnika sprężystości k oraz odkształcenia x, według wzoru:
Ep = 1/2 k x²
Gdy sprężyna ma współczynnik sprężystości równy 200 N/m i jest rozciągnięta o 0,1 m, jej energia potencjalna wynosi 1 J,
energia potencjalna elektryczna: Dla ładunku q umieszczonego w polu elektrycznym o potencjale V, stosujemy wzór:
Ep = q · V
Przykład: dla ładunku 2 C w polu o potencjale 5 V, energia potencjalna wynosi 10 J.

Te przykłady pokazują praktyczne zastosowania wzorów obliczających energię potencjalną w różnych obszarach fizyki. Uwzględnienie takich parametrów jak masa, wysokość, współczynnik sprężystości, odkształcenie, ładunek elektryczny oraz potencjał elektryczny jest niezbędne do właściwego kalkulowania energii potencjalnej.

Jak energia potencjalna wiąże się z pracą i siłą?

Energia potencjalna jest ściśle związana z pracą, którą wykonują siły zachowawcze. Te siły działają, gdy obiekt przemieszcza się pomiędzy dwoma punktami w polu sił. Mechaniczna praca, jaką wykazuje siła zachowawcza, odpowiada zmianie energii potencjalnej danego obiektu.

Na przykład, siła grawitacji jest doskonałym przykładem siły zachowawczej. Gdy podnosimy lub opuszczamy przedmiot, praca, która jest przy tym wykonywana, przekłada się na zmianę energii potencjalnej grawitacyjnej. Podobnie działają sprężyny — siła sprężystości, która pojawia się w odkształconych sprężynach, również należy do sił zachowawczych, a jej praca jest związana z energią potencjalną sprężystości.

Siły niezachowawcze, takie jak tarcie, funkcjonują w odmienny sposób. One nie tylko rozpraszają energię, ale również nie wpływają na mierzenie energii potencjalnej. Dzięki temu możemy stwierdzić, że energia potencjalna odzwierciedla pracę wykonaną przez siły zachowawcze podczas przemieszczenia obiektu w polu sił.

Związek energii potencjalnej z pracą wykonaną przez siły zachowawcze

Wykonywana praca przez siły zachowawcze, takie jak ciężar czy sprężystość, odpowiada zmianie energii potencjalnej obiektu między dwoma punktami. To oznacza, że zmiany w energii potencjalnej mają bezpośredni wpływ na pracę mechanicznych sił. Interesujące jest to, że w obrębie sił zachowawczych, praca wykonana przez nie nie zależy od ścieżki, jaką pokonuje ciało, ale wyłącznie od jego początkowej i końcowej pozycji.

Dzięki temu energia potencjalna staje się funkcją zależną od położenia. Oznacza to, że ona ilustruje możliwość wykonania pracy przez te siły, gdy obiekt przemieszcza się z jednego miejsca do drugiego. Ten związek podkreśla kluczową rolę energii potencjalnej w mechanice klasycznej, a także jej silną korelację z siłami i pracą, jaką te siły produkują.

Jak energia potencjalna przekształca się w inne formy energii?

Energia potencjalna zmienia się w energię kinetyczną w momencie ruchu ciała. Na przykład, gdy obiekt opada, jego potencjalna energia grawitacyjna ulega zmniejszeniu, jednocześnie wzrastając energia kinetyczna. To zjawisko doskonale pokazuje zasadę zachowania energii. W mechanicznych układach suma obu rodzajów energii — potencjalnej i kinetycznej — pozostaje niezmieniona, chyba że działają na nie siły, które nie są zachowawcze.

Inny przykład to sprężyna. Kiedy sprężyna powraca do swojego stanu równowagi, energia potencjalna związana z jej rozciągnięciem przemienia się w energię kinetyczną. Tego typu przekształcenia są niezwykle istotne w wielu urządzeniach, które wykorzystują siły zachowawcze, co umożliwia skuteczne gospodarowanie energią mechaniczną.

Zrozumienie tych procesów otwiera przed nami nowe możliwości efektywnego wykorzystania energii w różnorodnych rozwiązaniach technologicznych.

Transformacja energii potencjalnej w kinetyczną

Energia potencjalna przekształca się w kinetyczną w momencie, gdy obiekt zmienia swoje położenie. Na przykład, gdy coś spada z wysokości, jego grawitacyjna energia potencjalna zamienia się w energię kinetyczną, co sprawia, że prędkość tego obiektu rośnie.

Podobnie, w przypadku sprężyny, kiedy jest ona rozprężana, energia potencjalna sprężystości również przekształca się w energię kinetyczną powiązaną z obiektem.

W sytuacjach, gdzie działają wyłącznie siły zachowawcze, całkowita energia potencjalna oraz kinetyczna pozostaje niezmienna. Według zasady zachowania energii, zmiany w energii potencjalnej są skorelowane ze zmianami w energii kinetycznej.

Rola energii potencjalnej w elektrowniach wodnych i sprężynach

Energia potencjalna grawitacyjna, zgromadzona w elektrowniach wodnych, to moc, którą woda zdobywa na znacznej wysokości. Gdy woda spada, ta nagromadzona energia przekształca się w energię kinetyczną. To właśnie ta energia mechaniczna napędza turbiny, a one z kolei generują energię elektryczną dzięki pracy generatorów.

Z kolei w sprężynach energia potencjalna sprężystości powstaje wskutek deformacji mechanicznej. Sprężyna jest w stanie zmagazynować energię, a gdy zostaje zwolniona, ta energia przejawia się w postaci ruchu lub innego rodzaju pracy.

Obydwa te przykłady ilustrują, jak skutecznie można przekształcać energię potencjalną, aby produkować energię elektryczną lub wykonywać różnorodne prace mechaniczne.

Kiedy energia potencjalna osiąga ekstremum?

Energia potencjalna osiąga swoje skrajne wartości, zarówno maksimum, jak i minimum, w punktach równowagi danego systemu. To właśnie tam siły oddziałujące na obiekt wzajemnie się znoszą. W tych momentach gradient energii potencjalnej wynosi zero, co oznacza, że nie istnieje netto siła działająca na dany obiekt. Te ekstrema mają kluczowe znaczenie podczas analizy stabilności zarówno układów mechanicznych, jak i pól sił.

Warto również zwrócić uwagę na to, że:

punkt odniesienia jest kwestią wyboru,
poziom energii potencjałnej jest kwestią wyboru,
wpływają na wartość energii,
nie mają wpływu na zmiany sił w systemie,
ani na charakterystykę sił działających w systemie.

Punkt odniesienia i poziom odniesienia energii potencjalnej

Punkt odniesienia dla energii potencjalnej to umowna wysokość, od której określamy wartość potencjału w danym polu sił, na przykład w polu grawitacyjnym. Ten poziom można ustalić dowolnie, co daje nam elastyczność — możemy wybrać go na przykład jako powierzchnię Ziemi lub inną, wyznaczoną wysokość. Energii potencjalnej zawsze przypisuje się wartość w odniesieniu do tego konkretnego punktu.

Choć poziom odniesienia ma wpływ na wartość energii potencjalnej, to różnica tej energii między dwoma punktami pozostaje niezmienna, niezależnie od naszego wyboru. Oznacza to, że zmiana energii potencjalnej między dwoma miejscami jest stała, co ułatwia obliczenia dotyczące pracy wykonanej przez siły oraz przemiany energii, zapewniając spójność i jednoznaczność.

Jakie są zastosowania energii potencjalnej?

Energia potencjalna znajduje szerokie zastosowanie zarówno w codziennym życiu, jak i w różnych dziedzinach nauki. Spotykamy ją w tak prozaicznych przedmiotach jak:

sprężyny,
napięte łuki,
ugięte trampoliny,
a nawet w elastycznych gumkach recepturkowych.

W technice, szczególnie w elektrowniach wodnych, energia potencjalna grawitacyjna jest kluczowym elementem. W tym kontekście przekształca energię wody w energię elektryczną. W obszarze fizyki oraz astronomii ma ona fundamentalne znaczenie, umożliwiając analizę ruchu ciał niebieskich, a także obliczanie ich orbit i prędkości koniecznych do opuszczenia danego obiektu.

To jednak nie koniec jej możliwości. Technika grawitacyjnej asysty wykorzystuje potencjał tej energii do zmiany trajektorii statków kosmicznych, co może być kluczowe dla eksploracji kosmosu. Dodatkowo, badania nad czarnymi dziurami opierają się na analizie ich pola grawitacyjnego, co również wiąże się z energią potencjalną.

Przykłady z życia codziennego i techniki

Energia potencjalna jest wszechobecna w naszym codziennym życiu i ma wiele zastosowań w różnych obszarach technologii. Oto kilka przykładów:

rozciągnięta sprężyna gromadzi energię, gdy jest napięta,
napięty łuk, używany do strzałów, również skrywa energię,
ugięta trampolina akumuluje energię sprężystości, którą uwalnia, gdy wraca do pierwotnego kształtu,
naciągnięcie gumki recepturki przekształca tę energię w ruch.

W dziedzinie technologii, zwłaszcza w elektrowniach wodnych, energia potencjalna grawitacyjna odgrywa istotną rolę. Woda zgromadzona na dużej wysokości dysponuje znaczną ilością energii potencjalnej. Kiedy woda spada, ta energia zmienia się w energię kinetyczną, a następnie przekształca w energię elektryczną, produkowaną przez turbiny.

Wszystkie te przykłady ukazują, jak ważna jest energia potencjalna dla magazynowania oraz efektywnego przetwarzania energii w różnych gałęziach przemysłu.

Zastosowanie w fizyce i astronomii

Energia potencjalna odgrywa niezwykle istotną rolę zarówno w fizyce, jak i w astronomii. Umożliwia nam dogłębne zrozumienie ruchu obiektów grawitacyjnie związanych, takich jak:

planety,
księżyce,
satellity.

Na przykład, potrafimy obliczyć prędkość ucieczki – minimalną szybkość, która jest wymagana, by dany obiekt mógł opuścić pole grawitacyjne ciał niebieskich.

Co więcej, wiedza na temat pierwszej i drugiej prędkości kosmicznej ma kluczowe znaczenie podczas planowania trajektorii lotów oraz startów pojazdów kosmicznych. Zastosowanie techniki grawitacyjnej asysty polega na wykorzystaniu zmian energii potencjalnej obiektów astronomicznych, co pozwala na zwiększenie prędkości statków kosmicznych bez konieczności tankowania dodatkowym paliwem.

Dodatkowo, energia potencjalna jest niezwykle istotna dla badań nad czarnymi dziurami oraz dynamiką innych ciał w przestrzeni kosmicznej. Dzięki temu zyskujemy lepsze zrozumienie ich ruchów i interakcji w kosmosie. Badania te prowadzą nas ku odkrywaniu tajemnic wszechświata.

Jakie są różnice między energią potencjalną a kinetyczną?

Energia potencjalna to forma energii, która gromadzi się w obiektach w zależności od ich położenia lub stanu. Z kolei energia kinetyczna jest związana z ruchem, a jej wartość determinowana jest przez prędkość poruszającego się ciała. Można więc powiedzieć, że energia potencjalna jest bardziej statyczna, podczas gdy energia kinetyczna jest dynamiczna.

Te dwie formy energii mają zdolność do przemiany jedna w drugą. Na przykład, gdy przedmiot spada swobodnie, jego energia potencjalna przekształca się w energię kinetyczną. W przypadku zamkniętego systemu całkowita energia mechaniczna, czyli suma obu rodzajów energii, pozostaje niezmienna. Dzieje się tak dzięki zasadzie zachowania energii.

Różnice między energią potencjalną a kinetyczną dotyczą także ich źródła:

energia potencjalna zależy od miejsca, w którym się znajduje obiekt,
energia kinetyczna jest wynikiem ruchu, który ten obiekt wykonuje.

Dlaczego zasada zachowania energii jest istotna przy energii potencjalnej?

Zasada zachowania energii jest niezwykle ważna dla zrozumienia energii potencjalnej. Umożliwia nam ona dokładne śledzenie zmian energii w zamkniętych układach. Mówi, że całkowita energia mechaniczna, będąca sumą energii potencjalnej i kinetycznej, pozostaje na stałym poziomie, o ile nie działają siły niezachowawcze, takie jak tarcie.

Korzystając z tej zasady, energia potencjalna może przekształcać się w energię kinetyczną i vice versa, przy pełnym zachowaniu energii. Ta cecha jest szczególnie cennym narzędziem w obliczeniach dotyczących ruchu ciał oraz w analizie dynamiki układów mechanicznych. Co więcej, zasada ta stanowi fundament wielu zjawisk zarówno w inżynierii, jak i fizyce, gdzie precyzyjne bilanse energetyczne odgrywają kluczową rolę.

Respektowanie zasady zachowania energii zapewnia, że energia potencjalna jest wykorzystywana w sposób efektywny i nie znika w trakcie przemian.