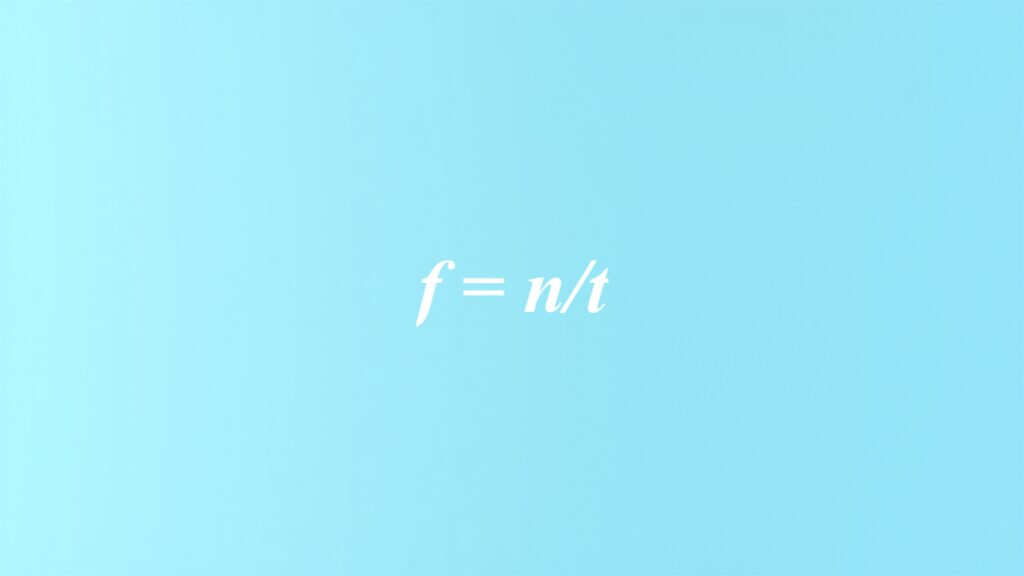Wzór na częstotliwość

Częstotliwość to istotna wielkość fizyczna, która wskazuje, ile drgań lub cykli występuje w danym zjawisku okresowym w ciągu jednostki czasu, zazwyczaj w jednej sekundzie. Stanowi kluczowy element w takich zjawiskach jak: ruch drgający, harmoniczny, obrotowy, a także różnorodne cykle, które można zaobserwować w: falach dźwiękowych czy w oscylacjach.

Interesującą cechą częstotliwości jest jej odwrotność w stosunku do okresu drgań. Krótszy okres wiąże się z wyższą częstotliwością. W matematyce istnieją różne wzory, które pomagają w obliczeniach związanych z częstotliwością, takie jak:

f = n/t, gdzie n oznacza liczbę drgań, a t czas,
f = 1/T, gdzie T to okres drgań,
f = ω/(2π), w którym ω oznacza prędkość kątową.

W dziedzinie fizyki częstotliwość ma kluczowe znaczenie zarówno w analizie zjawisk cyklicznych, jak i tych związanych z mechaniką kwantową. Dzięki niej możemy lepiej zrozumieć różnorodne zjawiska i ich szerokie zastosowanie.

Jakie są jednostki częstotliwości?

Jednostka miary częstotliwości w systemie SI to herc (Hz), co oznacza jeden cykl na sekundę. Dzięki tej prostszej definicji możemy łatwo określić, ile razy dana czynność powtarza się w ciągu sekundy.

Oprócz herca, istnieje także szereg jednostek pochodnych, które umożliwiają bardziej precyzyjne przedstawienie częstotliwości w różnych zakresach:

miliherc (mHz) – jedna tysięczna herca, stosowany w obszarze bardzo niskich częstotliwości,
kiloherc (kHz) – tysiąc herców,
megaherc (MHz) – milion herców,
gigaherc (GHz) – miliard herców,
teraherc (THz) – bilion herców.

Taki bogaty zestaw jednostek umożliwia dokładne wyrażanie częstotliwości. Od niskich dźwięków po fale elektromagnetyczne, na różnorodność zastosowań w technologii i fizyce, każda jednostka ma swoje specyficzne przeznaczenie.

Czym jest herc (Hz)?

Herc (Hz) jest jednostką częstotliwości w systemie SI. Wskazuje, ile razy dane zjawisko okresowe występuje w ciągu jednej sekundy. Kiedy mówimy o jednym hercu, mamy na myśli, że dane zjawisko zdarza się dokładnie raz na sekundę.

Nazwa tej jednostki zawdzięczamy Heinrichowi Hertzowi, który był pionierem w badaniach dotyczących fal elektromagnetycznych. Herc znajduje zastosowanie w wielu dziedzinach, takich jak:

drgania mechaniczne,
w fale dźwiękowe,
w fale elektromagnetyczne,
w różne ruchy obrotowe.

Dzięki swojej wszechstronności, jest on uniwersalnym narzędziem do pomiaru częstotliwości, stosowanym w różnych obszarach nauki i technologii.

Przeliczanie: mHz, kHz, MHz, GHz, THz

Przeliczanie jednostek częstotliwości polega na zastosowaniu dziesiętnych mnożników. Na przykład:

miliherc (mHz) odpowiada 10^-3 Hz,
kiloherc (kHz) to 10³ Hz,
megaherc (MHz) wynosi 10⁶ Hz,
gigaherc (GHz) to 10⁹ Hz,
teraherc (THz) osiąga 10¹² Hz.

Dzięki tym konwersjom, przeliczanie częstotliwości staje się proste i intuicyjne. Dla lepszego zobrazowania:

1 kHz to 1000 Hz,
1 MHz można przyrównać do miliona herców.

Takie przeliczenia mają ogromne znaczenie w wielu dziedzinach, w tym telekomunikacji, gdzie sygnały radiowe są często wyrażane w megahercach lub gigahercach. W akustyce oraz czasie badania promieniowania elektromagnetycznego wykorzystuje się jednostki od miliherców aż po teraherce. Zrozumienie tych mnożników pozwala na błyskawiczne i dokładne porównywanie wartości częstotliwości na różnych poziomach.

Jak wygląda podstawowy wzór na częstotliwość?

Podstawowa definicja częstotliwości sprowadza się do liczby drgań (n) w określonym czasie (t). To można ująć w formie równania f = n/t, co wskazuje, ile cykli odbywa się co sekundę.

Innym istotnym wzorem jest f = 1/T, gdzie T odnosi się do okresu drgań, czyli czasu, na który przypada jeden cykl.

W przypadku ruchu obrotowego częstotliwość można również wyrazić za pomocą f = ω/(2π). W tym równaniu ω oznacza pulsację, czyli prędkość kątową, a 2π reprezentuje wartość jednego pełnego obrotu.

Dzięki tym trzem równaniom możemy precyzyjnie obliczać częstotliwość w różnych obszarach fizyki, takich jak:

ruch harmoniczny,
ruch obrotowy.

Wzór f = n/t: liczba drgań i czas

Wzór f = n/t wyraża częstotliwość (f) jako relację pomiędzy liczbą drgań (n) a czasem (t), w którym te drgania miały miejsce. Innymi słowy, częstotliwość informuje nas o tym, ile drgań występuje w danym okresie, najczęściej mierzonym w sekundach.

Metoda ta ma szerokie zastosowanie w pomiarze i obliczaniu częstotliwości zjawisk cyklicznych, takich jak:

ruchy drgające,
fale,
oscylacje.

Przez dokładne zliczenie liczby drgań oraz czasu należycie możemy ustalić, jak często dane zjawisko się powtarza.

Wzór f = n/t stanowi istotne narzędzie w analizie ruchów cyklicznych. Wykorzystując go, możemy precyzyjnie obliczyć częstotliwość w wielu różnych kontekstach fizycznych.

Wzór f = 1/T: związek częstotliwości z okresem

Wzór f = 1/T ilustruje zależność, według której częstotliwość f jest odwrotnością okresu T. Okres to czas, który potrzeba na wykonanie jednego pełnego cyklu drgań, a jego jednostką jest sekunda.

Relacja między tymi dwoma pojęciami jest zrozumiała:

im krócej trwa drganie, tym wyższa częstotliwość,
częstotliwość, mierzona w hercach (Hz), określa liczbę pełnych cykli, które zachodzą w ciągu jednej sekundy,
dzięki temu wzorowi łatwo można dokonać konwersji okresu na częstotliwość.

To stanowi nieocenione narzędzie w badaniach ruchów cyklicznych.

Wzór f = omega/(2π): zależność z prędkością kątową

Wzór f = ω/(2π) ilustruje związek między częstotliwością liniową f a pulsacją ω, która to pulsacja oznacza prędkość kątową wyrażoną w radianach na sekundę. Pulsacja pełni rolę miary częstotliwości kołowej, a zatem związana jest ściśle z ruchem obrotowym. Przekształcając ten wzór, jesteśmy w stanie obliczyć klasyczną częstotliwość drgań lub obrotów, wyrażoną w hercach (Hz), przy użyciu wartości prędkości kątowej.

Takie obliczenia okazują się niezwykle przydatne w zrozumieniu dynamiki ruchu obrotowego oraz drgań harmonicznych. W obydwu przypadkach, obiekt porusza się po okręgu z ustaloną prędkością kątową, a zastosowanie tego wzoru pozwala nam na lepszą analizę wielu aspektów tych zjawisk.

Kiedy stosuje się wzór na częstotliwość?

Wzór na częstotliwość odgrywa istotną rolę w opisie zjawisk okresowych, takich jak ruch drgający czy harmoniczny. Definiuje liczbę drgań występujących w danym czasie. Jest także kluczowy dla analizy częstotliwości kołowej w ruchu obrotowym, umożliwiając obliczenie prędkości kątowej.

W dziedzinie akustyki i muzyki, formuła ta pozwala lepiej zrozumieć:

drgania strun,
fale dźwiękowe generowane przez instrumenty,
zastosowanie w badaniach fal elektromagnetycznych i mechanicznych.

Ponadto, ma ogromne znaczenie w różnych eksperymentach i pomiarach naukowych.

Ruch drgający i drgania harmoniczne

Ruch drgający to sposób, w jaki nasze ciało porusza się wokół ustalonej pozycji równowagi. Cechuje się on regularnymi wychyleniami zachodzącymi w czasie. Amplituda odnosi się do maksymalnego wychylenia od tej stabilnej pozycji, natomiast okres drgań to czas, który jest potrzebny do przeprowadzenia jednego pełnego cyklu ruchu.

Drgania harmoniczne są szczególnym rodzajem ruchu drgającego. W tym przypadku siła przywracająca jest proporcjonalna do wychylenia i działa w stronę przeciwną. Dzięki temu, ruch przyjmuje charakter sinusoidy. Klasycznymi przykładami takich drgań są:

wahadło matematyczne,
ciężarek zawieszony na sprężynie.

Częstotliwość drgań harmonicznych wskazuje, ile pełnych cykli pojawia się w określonym czasie. Można to obliczyć za pomocą wzorów:

f = n/t, gdzie n oznacza liczbę drgań, a t to czas,
f = 1/T, gdzie T oznacza okres drgań.

W przypadku wahadła, częstotliwość głównie zależy od długości ramienia, podczas gdy w przypadku ciężarka na sprężynie kluczowa jest stała sprężystości.

Warto zauważyć, że amplituda drgań wpływa jedynie na maksymalne wychylenie, nie mając wpływu na częstotliwość ruchu harmonicznego.

Ruch obrotowy i częstotliwość kołowa

W ruchu obrotowym częstotliwość wskazuje, ile pełnych obrotów wykonuje obiekt w określonym czasie, najczęściej w sekundzie. Okres tego ruchu to czas potrzebny do zrealizowania jednego pełnego obrotu. Z kolei częstotliwość kołowa, znana jako pulsacja (ω), dotycząca prędkości kątowej, mierzy się w radianach na sekundę.

Pomocny w zrozumieniu relacji między częstotliwością (f) a pulsacją (ω) jest wzór: f = ω/(2π). Pozwala on zamienić prędkość kątową na liczbę obrotów na sekundę. Jest to niezwykle ważne przy analizie ruchu obrotowego, zwłaszcza w obszarach takich jak fizyka i inżynieria. Dzięki tym informacjom możemy precyzyjniej określić dynamikę obrotów w maszynach, a także w elementach systemów elektromagnetycznych.

Drgania w instrumentach muzycznych i falach dźwiękowych

Drgania w instrumentach muzycznych powstają głównie wskutek wibracji strun. Kluczowe znaczenie mają przy tym ich długość, masa oraz napięcie. Te akustyczne fale przekładają się na pudło rezonansowe, co prowadzi do wzmocnienia dźwięku, zwiększając jego głośność oraz barwę.

Fala dźwiękowa przemierza przestrzeń z określoną prędkością, a częstotliwość drgań struny warunkuje wysokość tonu. Rezonans znacząco wpływa na jakość dźwięku, intensyfikując wybrane częstotliwości. Dodatkowo, zjawisko dudnienia pojawia się, gdy dwa zbliżone tony nakładają się na siebie, powodując wahania głośności, które są wyczuwalne dla naszego ucha.

Przykładem urządzenia, które wykorzystuje zjawisko rezonansu, jest rezonator Helmholtza. Służy on do generowania lub wzmacniania konkretnej częstotliwości dźwiękowej. Takie zjawiska znajdują szerokie zastosowanie nie tylko w instrumentach muzycznych, ale także w akustyce jako takiej.

Co oznacza okres i jak wpływa na częstotliwość?

Okres drgań (T) to czas potrzebny na dokonanie jednego pełnego cyklu ruchu okresowego, a jego jednostką jest sekunda. Zachodzi między nim a częstotliwością związek odwrotny, który można przedstawić za pomocą wzoru f = 1/T. Tutaj f reprezentuje częstotliwość, natomiast T oznacza okres.

Warto zauważyć, że:

im krótszy jest okres, tym wyższa częstotliwość,
oznacza to, że drgania lub inne procesy powtarzają się w szybszym tempie,
okres odgrywa istotną rolę w analizie ruchów drgających,
przykładami są matematyczne wahadło czy ciężar zawieszony na sprężynie,
zrozumienie tego parametru umożliwia precyzyjne obliczenie częstotliwości danego zjawiska.

Jak zmierzyć i obliczyć częstotliwość?

Pomiar częstotliwości polega na zliczaniu liczby drgań w określonym czasie, a także na precyzyjnym odmierzaniu tego czasu. Do tego celu wykorzystuje się manualny stoper, który pozwala dokładnie ustalić, jak długo trwają poszczególne cykle drgań. W takich eksperymentach najczęściej korzysta się z wahadła. Kulka zamocowana na nici, zawieszona na statywie, ułatwia zarówno obserwację, jak i liczenie drgań.

Aby obliczyć częstotliwość, stosujemy wzór f = n/t, gdzie n to liczba zanotowanych drgań, a t oznacza całkowity czas ich trwania. Kluczowym aspektem pomiaru jest również uwzględnienie niepewności, która może być wynikiem błędów wliczania drgań, pomiaru czasu oraz wpływów z otoczenia, takich jak drgania podłoża. Aby zminimalizować te błędy, warto powtarzać doświadczenie oraz korzystać ze stabilnego statywu, który utrzymuje układ pomiarowy w nienaruszonym stanie.

W praktyce najlepsze rezultaty osiąga się, mierząc czas dla większej liczby drgań, na przykład 10 lub 20. Taki sposób postępowania znacząco redukuje wpływ błędów jednego cyklu na obliczoną częstotliwość. Wynik końcowy wyraża się w hercach (Hz), co odnosi się do liczby drgań na sekundę. Pomiar oraz obliczanie częstotliwości są niezwykle istotne w analizie ruchów drgających i falowych, znajdując zastosowanie w wielu dziedzinach.

Pomiar liczby drgań i czasu

Pomiar liczby drgań oraz czasu to proces, który obejmuje zliczanie pełnych cykli ruchu drgającego oraz rejestrowanie czasu ich trwania. Można do tego wykorzystać stopery lub bardziej zaawansowane urządzenia pomiarowe. Istotna jest precyzyjność zarówno w zliczaniu drgań, jak i w długości trwania obserwacji, ponieważ wpływa ona na dokładność ostatecznych rezultatów.

W kontekście doświadczeń szkolnych, jak na przykład z wahadłem matematycznym czy ciężarkiem umieszczonym na sprężynie, zebrane dane dotyczące:

liczby drgań,
zmierzonego czasu,
częstotliwości fali.

Odgrywają kluczową rolę w obliczaniu częstotliwości. Umożliwia to określenie liczby drgań na sekundę, co stanowi definicję częstotliwości. Wzór do obliczeń to f = n/t, gdzie n oznacza liczbę drgań, a t to odnotowany czas ich trwania.

Obliczanie niepewności pomiaru

Niepewność w pomiarze częstotliwości jest efektem różnorodnych błędów, które mogą pojawić się podczas liczenia drgań oraz mierzenia czasu. Dodatkowo, istotną rolę odgrywają czynniki zewnętrzne, takie jak zmiany w amplitudzie czy specyfika warunków, w których przeprowadzane są eksperymenty. Aby właściwie określić niepewność pomiarową, istotne jest uwzględnienie precyzji używanych narzędzi, a także analiza powtarzalności uzyskiwanych wyników.

W zastosowaniach praktycznych najczęściej wykorzystuje się metody statystyczne:

szacowanie rozrzutu wyników pomiarów,
określenie jak bardzo mogą one odbiegać od prawdziwej wartości,
ocenę rzetelności pomiarów,
optymalizację technik eksperymentalnych,
minimalizację błędów w pomiarach częstotliwości.

Jak długość wahadła oraz masa wpływa na częstotliwość?

Częstotliwość drgań wahadła matematycznego jest ściśle związana z jego długością. To zjawisko można ukazać za pomocą wzoru, który wskazuje, że częstotliwość ma związek z pierwiastkiem z odwrotności długości. Oznacza to, że krótsze wahadła mają tendencję do charakteryzowania się wyższą częstotliwością drgań. Co istotne, masa wahadła nie wpływa na tę częstotliwość, co stanowi niezwykłą cechę tego typu ruchu.

Dodatkowo, fenomen izochronizmu powoduje, że okres drgań pozostaje niezmienny, niezależnie od wielkości amplitudy. Dzięki temu zjawisku możliwe jest uzyskanie precyzyjnych i powtarzalnych pomiarów częstotliwości, co ma ogromne znaczenie w eksperymentalnych badaniach.

Wzory dla wahadła matematycznego

Wzór na okres drgań wahadła matematycznego jest następujący: T = 2π√(L/g). W tym równaniu L reprezentuje długość wahadła, natomiast g to przyspieszenie ziemskie, które wynosi około 9,81 m/s². Aby wyznaczyć częstotliwość, posługujemy się wzorem f = 1/T, co prowadzi nas do uproszczonej formy f = 1 / (2π√(L/g)).

Z tych zależności wynika, że częstotliwość drgań wahadła zależy jedynie od jego długości oraz stałej grawitacyjnej. Co istotne, masa wahadła nie ma żadnego znaczenia. Wahadło matematyczne stanowi podstawowy model dla zachowań drgających. Znajduje ono zastosowanie w eksperymentach fizycznych, gdzie badane są różnorodne właściwości oscylacji.

Warto również zauważyć, że:

im dłuższe jest wahadło, tym niższa częstotliwość jego drgań,
długość wahadła ma odwrotny wpływ na częstość drgań.

Czy masa wahadła wpływa na częstotliwość?

Masa wahadła matematycznego nie ma wpływu na jego częstotliwość drgań. Ta zależy wyłącznie od:

długości wahadła,
wartości przyspieszenia ziemskiego.

Żadnego związku z masą nie ma. Równanie opisujące okres drgań nie uwzględnia masy, co jasno pokazuje, że zmiana masy nie ma żadnego wpływu na częstotliwość drgań.

Warto pamiętać, że jedynie długość oraz przyspieszenie decydują o tym, w jakim tempie wahadło się porusza. Reasumując, masa nie wpływa na drgania, co może być zaskakujące, ale kluczowe dla zrozumienia ruchu wahadła.

Jak długość fali oraz prędkość wpływają na częstotliwość?

Częstotliwość fali można obliczyć za pomocą równania f = v/λ. W tym wzorze f to częstotliwość, v oznacza prędkość fali, a λ to długość fali. Długość fali to po prostu odległość między kolejnymi szczytami lub dołkami fali, natomiast prędkość fali zależy od właściwości medium, przez które się przemieszcza.

Kiedy długość fali rośnie przy stałej prędkości, częstotliwość spada. Wynika to z faktu, że ta sama fala zajmuje większą przestrzeń. Przykładowo, jeśli prędkość fali zwiększa się, a długość fali pozostaje niezmienna, częstotliwość wzrasta.

Te zmiany parametrów mają bezpośredni wpływ na częstotliwość, co jest istotne w analizie fal, zarówno mechanicznych, jak i elektromagnetycznych. Zrozumienie powiązań między długością fali, prędkością a częstotliwością jest kluczowe dla precyzyjnych obliczeń w dziedzinach takich jak akustyka, optyka czy elektronika.

Powiązanie częstotliwości z długością i prędkością fali

Częstotliwość fali (f) jest ściśle związana z jej prędkością (v) oraz długością (λ). Możemy to przedstawić w prosty sposób dzięki wzorowi: f = v/λ. Długość fali, z kolei, to odległość między dwoma sąsiadującymi punktami, które drgają w tej samej fazie.

Warto pamiętać, że prędkość fali uzależniona jest od charakterystyki medium, przez które się porusza. Do najważniejszych czynników wpływających na prędkość fali należą:

gęstość medium,
sprężystość medium,
temperatura medium.

Jeśli prędkość fali wzrasta, to przy zachowaniu stałej długości fali, następuje również wzrost częstotliwości. Natomiast, gdy fala staje się dłuższa, częstotliwość maleje, o ile prędkość nie ulega zmianie.

Te relacje mają ogromne znaczenie w badaniach różnych typów fal, takich jak:

w fale dźwiękowe,
w fale świetlne,
w fale elektromagnetyczne.

Zmiany w długości oraz prędkości fali wpływają na jej zachowanie i percepcję w różnych kontekstach.

Jaki jest związek częstotliwości z energią fotonu?

Energia fotonu jest ściśle powiązana z częstotliwością fali elektromagnetycznej. Relację tę wyraża równanie E = h·f, gdzie:

E oznacza energię fotonu,
h to stała Plancka, która wynosi około 6,626 × 10⁻³⁴ J·s,
f to częstotliwość fali mierzona w hercach (Hz).

Im wyższa częstotliwość fal, tym większa energia pojedynczego fotonu. To zjawisko stanowi trzon wielu teorii w fizyce kwantowej. Zrozumienie tej zależności jest kluczowe, szczególnie w kontekście badania promieniowania elektromagnetycznego, jak na przykład promieni gamma, które charakteryzują się ekstremalnie wysokimi częstotliwościami oraz energią.

Dzięki równaniu E = hν, naukowcy mogą łatwo obliczyć energię pojedynczego kwantu światła, korzystając z jego częstotliwości. Takie podejście pozwala na głębsze zrozumienie właściwości fotonów oraz ich wpływu na różne zjawiska w dziedzinie fizyki.

Wzór E = hν

Wzór E = hν (czyli E = h·f) definiuje energię fotonu, która powstaje na skutek mnożenia stałej Plancka (h) przez częstotliwość fali (ν lub f). Wartość tej stałej wynosi około 6,626 × 10⁻³⁴ J·s i stanowi fundamentalny element w dziedzinie fizyki kwantowej.

Interesujące jest to, że energia fotonu zwiększa się wraz z wyższą częstotliwością fali elektromagnetycznej. W praktyce oznacza to, iż fale o większej częstotliwości zawierają więcej energii. Opisany wzór jest również podstawą do zrozumienia różnorodnych zjawisk kwantowych, takich jak:

emisja światła,
absorpcja światła,
efekt fotoelektryczny.

Foton, traktowany jako najmniejsza jednostka energii światła – zwana też kwantem – ilustruje, jak bardzo ze sobą współgrają właściwości falowe i korpuskularne światła. Związek E = hν ukazuje ten fascynujący dualizm, który jest niezbędny do pełnego zrozumienia natury światła.

Jak częstotliwość jest wykorzystywana w analizie fal i akustyce?

Częstotliwość odgrywa niezwykle ważną rolę w analizie fal, zarówno dźwiękowych, jak i mechanicznych. Definiuje ona liczbę drgań lub cykli występujących w ciągu sekundy i ma kluczowy wpływ na wysokość dźwięku w akustyce. Na przykład, kiedy dwie fale o zbliżonych częstotliwościach się nachodzą, może wystąpić zjawisko dudnienia, co prowadzi do okresowego wzmocnienia i wygaszenia dźwięku.

Rezonans zachodzi, gdy system drga z częstotliwością bliską jego własnej. Zjawisko to jest podstawą działania rezonatora Helmholtza, który służy do selektywnej emisji fal o określonej częstotliwości. W kontekście fal radiowych, częstotliwość wpływa także na rozmiar strefy Fresnela, co ma kluczowe znaczenie dla jakości propagacji oraz emisji fal.

Z tych powodów można stwierdzić, że częstotliwość stanowi fundament zarówno w badaniach, jak i praktycznych zastosowaniach związanych z akustyką i falami.

Dudnienie, rezonans i rezonator Helmholtza

Dudnienie występuje, gdy dwie fale o zbliżonych, aczkolwiek nie identycznych częstotliwościach nakładają się na siebie. To zjawisko objawia się w postaci okresowych zmian głośności, które odczuwamy jako pulsujące lub drgające dźwięki.

Rezonans zachodzi, kiedy częstotliwość zewnętrznego wymuszenia idealnie odpowiada częstotliwości własnej układu. W rezultacie dochodzi do znacznego zwiększenia amplitudy drgań. Przykładem tego zjawiska jest rezonator Helmholtza – specjalny typ akustycznej wnęki, która generuje unikalną częstotliwość rezonansową. Ta częstotliwość uzależniona jest od:

kształtu wnęki,
objętości wnęki,
rozmiaru otworu.

Rezonator Helmholtza znajduje szerokie zastosowanie w selekcji oraz wzmacnianiu wybranych częstotliwości dźwiękowych. To zjawisko odgrywa kluczową rolę zarówno w dziedzinie akustyki, jak i muzyki. Wspólnym elementem łączącym wszystkie te fenomeny jest ich związek z częstotliwościami fal i drgań, które są fundamentalne dla ich zachowania oraz zastosowań.

Strefa Fresnela i emisja fali

Strefa Fresnela to elipsoidalna przestrzeń pomiędzy nadajnikiem a odbiornikiem fal, odgrywająca kluczową rolę w jakości sygnału radiowego. Zaskakujące jest, że wszelkie przeszkody i zakłócenia w obrębie tej strefy mogą znacząco osłabić sygnał. Interesującym aspektem jest fakt, że jej wielkość maleje wraz ze wzrostem częstotliwości. Oznacza to, że wyższe częstotliwości powodują zmniejszenie objętości strefy Fresnela, co w konsekwencji wpływa na sposób, w jaki fale się rozprzestrzeniają.

Emisja fali to proces, w którym powstają i rozchodzą się fale elektromagnetyczne lub akustyczne. Istotnym elementem tego procesu jest częstotliwość, która określa zachowanie fali oraz jej skuteczność w transmisji. Zrozumienie mechanizmów działania strefy Fresnela oraz wpływu częstotliwości na emisję fal jest niezbędne przy projektowaniu systemów komunikacyjnych i optymalizacji sygnału. Dodatkowo, lepsza znajomość tych zasad może przyczynić się do wprowadzenia skuteczniejszych rozwiązań w dziedzinie telekomunikacji.

Jakie są zastosowania praktyczne wzoru na częstotliwość?

wzór na częstotliwość to niezwykle użyteczne narzędzie w badaniu ruchu cyklicznego. Umożliwia on obliczenie liczby drgań lub obrotów w określonym czasie, co pozwala na analizę różnych rodzajów drgań mechanicznych, takich jak:

wahadło matematyczne,
ciężarek zawieszony na sprężynie.

To kluczowy element w zrozumieniu zjawisk harmonicznych w fisyce.

Ponadto, ten wzór z powodzeniem stosuje się także w kontekście analizy fal dźwiękowych oraz elektromagnetycznych. Takie podejście jest szczególnie ważne przy badaniu instrumentów muzycznych i sygnałów elektronicznych. W praktyce, podczas doświadczeń w szkołach i laboratoriach, wykorzystuje się go w połączeniu z różnymi instrumentami pomiarowymi, na przykład:

stoperami ręcznymi,
statywami.

Dzięki temu można z dużą precyzją określić częstotliwość drgań.

Otrzymane wyniki pomiarów nie tylko pomagają w weryfikacji teorii, ale także przyczyniają się do rozwijania umiejętności pomiarowych. Takie zastosowania ułatwiają zrozumienie podstawowych zjawisk fizycznych, a także rozwijają zdolności analizy danych oraz praktyczne wykorzystywanie matematycznych wzorów.

Analiza ruchu cyklicznego

Analiza ruchu cyklicznego dotyczy badania zjawisk, które powtarzają się w czasie, takich jak oscylacje, drgania i ruchy obrotowe. Dzięki tej metodzie możemy ustalić częstotliwość, czyli liczbę pełnych cykli występujących w danym okresie. Wzory używane do obliczania częstotliwości są kluczowe dla naszego zrozumienia dynamiki rozmaitych układów fizycznych oraz ich działania.

Tego rodzaju badania mają szerokie zastosowanie w:

fizyce,
inżynierii,
akustyce,
analizie fal elektromagnetycznych.
modelowaniu drgań.

Dodatkowo, ta forma analizy wspiera:

wykrywanie rezonansów,
optymalizację działania maszyn,
optymalizację instrumentów pomiarowych,
wzrost wydajności,
wzrost precyzji w wielu dziedzinach.

Instrumenty pomiarowe i doświadczenia szkolne

W szkolnych eksperymentach dotyczących częstotliwości korzystamy z podstawowych narzędzi pomiarowych. Do niezbędnego zestawu zaliczają się:

ręczny stoper,
statyw,
kulka,
nić.

Te proste przyrządy umożliwiają skonstruowanie wahadła matematycznego oraz precyzyjne określenie liczby drgań i czasu, przez jaki one zachodzą. Na tej podstawie możemy obliczyć częstotliwość, stosując wzór f = n/t.

Podczas tych eksperymentów zajmujemy się również ustalaniem niepewności pomiaru. Dzięki temu zyskujemy lepsze zrozumienie tego, jak różne czynniki mogą wpływać na dokładność naszych wyników. Takie doświadczenia okazują się niezwykle wartościowe. Uczniowie mają możliwość lepszego uchwycenia dynamiki ruchów okresowych oraz praktycznego zastosowania teoretycznych wzorów związanych z częstotliwością.