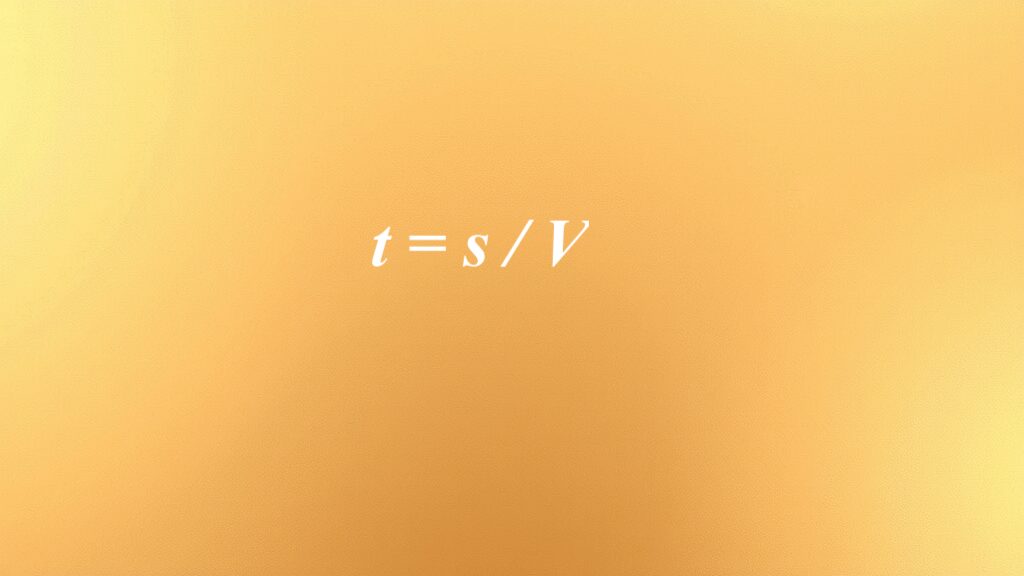Wzór na czas

Wzór na czas, wyrażony jako t = s / V, stanowi fundamentalne narzędzie w analizie ruchu. Dzięki niemu możemy obliczyć, jak długo trwa przemieszczanie się obiektu, gdy znamy:

pokonaną drogę (s),
prędkość (V),
czas (t).

Posługując się tym równaniem, możemy precyzyjnie ustalić, ile czasu zajmie podróż z jednego miejsca do drugiego, przy założeniu, że prędkość pozostaje stała.

Co istotne, ten wzór ma charakter odwrotnie proporcjonalny do prędkości. Innymi słowy, przy tej samej pokonanej drodze, większa prędkość oznacza skrócony czas podróży. Zrozumienie tej zależności jest kluczowe w edukacji fizycznej oraz w analizie ruchu w różnych dziedzinach, takich jak:

transport,
inżynieria,
planowanie tras transportowych.

W każdej z tych dziedzin umiejętne wykorzystanie tego wzoru może przynieść znaczące korzyści.

Jak wygląda zależność między drogą, prędkością a czasem?

Związek między drogą, prędkością a czasem można zrozumieć dzięki prostemu wzorowi: t = s / V. W tym równaniu czas (t) obliczamy, dzieląc długość przebytej trasy (s) przez prędkość (V). Tak więc, przy stałej prędkości, pokonanie większej odległości zajmie nam więcej czasu.

Prędkość daje nam wyobrażenie o tym, jak szybko porusza się dany obiekt, podczas gdy droga oznacza całkowitą długość trasy. Ta zależność jest istotna w kontekście ruchu jednostajnego prostoliniowego. Umożliwia nam precyzyjne określenie, ile czasu pochłonie przebycie konkretnego dystansu przy ustalonej prędkości średniej.

Co więcej, wzór ten ma zastosowanie w praktyce, na przykład przy:

planowaniu podróży,
szacowaniu czasu przejazdu,
niezależnie od tego, jakim środkiem transportu się poruszamy.

Jak stosować wzór na czas: t = s / v?

Wzór na czas, określający zależność t = s / v, przydaje się do obliczania, ile czasu zajmie pokonanie określonej odległości. By go zastosować, wystarczy podzielić przebytą drogę s przez prędkość v. Ważne jest, aby jednostki były spójne, na przykład odległość powinna być podana w kilometrach, a prędkość w kilometrach na godzinę. W przeciwnym razie uzyskany wynik czasu nie będzie miał sensu.

W praktyce taki wzór jest niezwykle przydatny podczas planowania podróży czy oszacowywania czasu przejazdu. Umożliwia dokładne określenie długości planowanej podróży. Kluczowe jest wcześniejsze ustalenie wartości drogi i prędkości:

podzielić przebytą drogę przez prędkość,
zapewnić spójność jednostek,
zastosować wzór t = s / v,
szacować czas przejazdu,
efektywnie zarządzać logistyką.

Działając według zasady dzielenia s przez v, można szybko uzyskać wynik, co z kolei wspiera efektywne zarządzanie czasem i logistyką. To narzędzie ma szczególne znaczenie, gdy chodzi o tworzenie harmonogramów oraz optymalizację tras.

Możliwość wykorzystania wzoru t = s / v sprawdza się zarówno w przypadku ruchu jednostajnego, jak i w badaniach dotyczących dynamiki pojazdów.

Jakie są wymagane jednostki dla czasu, drogi i prędkości?

Dla wzoru na czas, który wyraża się jako t = s / v, niezwykle istotne jest, aby używane jednostki były zgodne. Możemy mierzyć drogę (s) w:

metrach (m),
kilometrach (km).

Z kolei prędkość (v) powinna być określona w:

metrach na sekundę (m/s),
kilometrach na godzinę (km/h).

Czas (t) można zapisywać w różnych jednostkach, takich jak:

sekundy (s),
minuty (min),
godziny (h).

Gdy jednostki się różnią – na przykład gdy droga podana jest w kilometrach, a prędkość w metrach na sekundę – konieczne jest dokonanie przeliczeń, by uniknąć pomyłek. Zastosowanie spójnych jednostek to kluczowy element w prowadzeniu poprawnych obliczeń w fizyce i kinematyce, co przyczynia się do ich wiarygodności.

Jak przekształcać wzór na czas do obliczania drogi lub prędkości?

Wzór na czas, t = s / V, można dostosować do różnych sytuacji, wykorzystując znane dane. Aby znaleźć drogę, korzystamy z równania s = V · t, co oznacza, że droga to wynik mnożenia prędkości przez czas. Gdy chcemy określić prędkość, używamy wzoru V = s / t. W tej formule prędkość stanowi stosunek przebytej drogi do upływającego czasu.

Umiejętność przekształcania wzorów pozwala na większą elastyczność w obliczeniach, co jest kluczowe przy analizie ruchu jednostajnego. Takie zdolności stają się niezwykle pomocne, gdy zmagamy się z problemami związanymi z czasem, drogą i prędkością.

W jakich typach ruchu wykorzystuje się wzór na czas?

Wzór na czas znajduje swoje główne zastosowanie w ruchu jednostajnym prostoliniowym, gdzie prędkość jest niezmienna. Dzięki temu, możemy w prosty sposób obliczyć czas potrzebny na przejechanie określonej odległości. W takim przypadku, użycie formuły t = s / v jest skuteczne i precyzyjne.

Natomiast w sytuacji ruchu jednostajnie przyspieszonego, sama formuła staje się niewystarczająca. W miarę jak prędkość ulega zmianom, konieczne jest uwzględnienie przyspieszenia. W takich okolicznościach korzystamy z równań kinematyki, takich jak:

t = (v – v0) / a,
s = v0t + ½at².

Dlatego też wzór na czas najbardziej przydaje się podczas analizy ruchu o stałej prędkości. W przypadku przyspieszenia wykorzystujemy go jedynie do uzupełniających obliczeń, co pozwala lepiej zrozumieć zasady kinematyki.

Ruch jednostajny

Ruch jednostajny charakteryzuje się stałą prędkością, co sprawia, że czas trwania takiego ruchu można łatwo obliczyć za pomocą prostego wzoru: t = s / V. W tej formule t oznacza czas, s to pokonana droga, a V to prędkość.

Ten wzór ma fundamentalne znaczenie w kinematyce, ponieważ umożliwia szybkie ustalanie czasu dla ruchu prostoliniowego z niezmienną prędkością. Dokładność pomiaru czasu w ruchu jednostajnym jest wysoka, ponieważ prędkość pozostaje stała przez cały czas trwania ruchu.

Co więcej, ta formuła jest szeroko wykorzystywana w nauczaniu fizyki oraz w rozwiązywaniu problemów związanych z ruchem jednostajnym, szczególnie gdy dostępne są lub wymagane są informacje dotyczące drogi i prędkości.

Ruch przyspieszony

Ruch przyspieszony to rodzaj ruchu, w którym prędkość zmienia się w czasie z powodu działającego przyspieszenia. W tej sytuacji prędkość nie pozostaje stała, co oznacza, że klasyczny wzór t = s / v, znany z ruchu jednostajnego, nie wystarcza do dokładnych obliczeń czasu.

Aby uzyskać bardziej precyzyjne wyniki, korzystamy z równań kinematycznych. Te równania biorą pod uwagę nie tylko przyspieszenie, ale także prędkość początkową, co jest kluczowe w wielu dziedzinach, na przykład w dynamice pojazdów. Przy badaniu ruchu przyspieszonego ważne jest oszacowanie, jak długo trwa zmiana prędkości lub jaką drogę pojazd pokona, gdy jego prędkość się zmienia.

W takich sytuacjach przydatne są wzory związane z przyspieszeniem:

t = (v – v₀) / a, gdzie:
v to prędkość końcowa,
v₀ to prędkość początkowa,
a oznacza przyspieszenie.

Dzięki tym równaniom możemy dokładnie określić czas potrzebny na różne zjawiska związane z ruchem przyspieszonym.

Jak obliczyć czas dla różnych środków transportu?

Obliczanie czasu dla różnych środków transportu opiera się na prostym wzorze t = s / v. W tym równaniu, t oznacza czas, s to przebyta odległość, a v symbolizuje prędkość pojazdu. W praktyce prędkość oraz długość trasy są dostosowywane do specyfiki każdego środka transportu, uwzględniając na przykład różnorodne limity prędkości oraz warunki panujące na drodze.

Ponadto, analizując dynamikę pojazdów, często uwzględnia się zmienne dotyczące prędkości i przyspieszenia, co pozwala na dokładniejsze oszacowanie czasu przejazdu. Wykorzystanie tego wzoru w planowaniu podróży znacząco ułatwia przewidywanie czasów, co jest niezwykle istotne dla optymalizacji tras.

Taka precyzja przyczynia się także do zwiększenia efektywności różnych środków transportu, umożliwiając:

lepsze zaplanowanie czasu przejazdu,
ocenę wpływu transportu na czas podróży,
zmniejszenie zużycia energii.

Wzór na czas w analizie dynamiki pojazdów

Wzór na czas w analizie dynamiki pojazdów stanowi kluczowe narzędzie do określania czasu przejazdu. Obliczenia bazują na przebytej drodze oraz średniej prędkości, a podstawowa forma tego równania wyraża się jako t = s / v, gdzie t to czas, s oznacza drogę, a v to prędkość.

Kiedy jednak mówimy o pojazdach, które mogą zmieniać swoją prędkość – na przykład podczas przyspieszania czy hamowania – trzeba nieco rozbudować ten wzór. Istotne jest, aby uwzględnić zmiany prędkości w czasie. Pomimo tej dodatkowej złożoności, wzór stanowi podstawowe narzędzie do szybkiego oszacowania czasu przejazdu w przypadku ruchu jednostajnego.

Zrozumienie i umiejętność zastosowania tego wzoru może znacząco wpłynąć na optymalizację dynamiki pojazdów. Dzięki temu możliwe jest zwiększenie efektywności poruszania się oraz lepsze planowanie tras w transporcie. W dziedzinie analizy dynamiki pojazdów często korzysta się także z zaawansowanych modeli, które uwzględniają przyspieszenia. Niemniej jednak, podstawowy wzór t = s / v pozostaje punktem wyjścia dla tych bardziej skomplikowanych rozważań.

Przykład praktyczny: planowanie podróży i przewidywanie czasu przejazdu

Planowanie podróży to proces, który można uprościć dzięki zastosowaniu prostego wzoru do obliczania czasu przejazdu. Gdy znamy odległość naszej trasy oraz średnią prędkość, bardzo łatwo określamy, ile czasu spędzimy w drodze. Wzór t = s / v wskazuje, że „t” oznacza czas, „s” to dystans, a „v” to średnia prędkość. To narzędzie umożliwia zarówno kierowcom, jak i logistykom lepsze planowanie i wybór najdogodniejszych tras.

W Internecie znajdziemy wiele kalkulatorów czasu podróży, które znacznie ułatwiają te obliczenia. Dzięki nim możemy uwzględnić:

różnorodne warunki drogowe,
zmiany prędkości,
ważność estymacji czasu przejazdu.

Estymacja czasu przejazdu jest niezwykle ważna, ponieważ pozwala na:

efektywne zarządzanie harmonogramami,
ograniczenie opóźnień,
lepsze wykorzystanie środków transportu.

Co więcej, odpowiednie planowanie ma znaczący wpływ na efektywność podróży, co jest istotne zarówno w przypadku transportu osób, jak i przewozu towarów.

Jak wzór na czas wspiera zarządzanie czasem i efektywność energetyczną?

Wzór na czas odgrywa kluczową rolę w zarządzaniu czasem oraz w zwiększaniu efektywności energetycznej w sektorze transportu. Umożliwia dokładne oszacowanie czasu niezbędnego do przebycia określonej trasy, co znacząco ułatwia planowanie podróży i prognozowanie czasu przejazdu. Taki precyzyjny kalkulacje pomagają lepiej organizować harmonogramy oraz unikać nieprzewidzianych opóźnień.

Weźmy na przykład zależność między prędkością a czasem. Analizując ją, możemy ocenić efektywność użycia różnych środków transportu z perspektywy ich zużycia energii. Właściwa optymalizacja prędkości i czasu przelotów przyczynia się do obniżenia zużycia paliwa, co oczywiście prowadzi do oszczędności finansowych i ma korzystny wpływ na środowisko.

Dodatkowo, wykorzystując wzór na czas, możemy wprowadzać innowacyjne i bardziej energooszczędne rozwiązania oraz efektywniej korzystać z dostępnych zasobów transportowych. Taki sposób działania sprawia, że transport staje się bardziej efektywny, co przynosi korzyści dla nas wszystkich.

Ocena skuteczności środków transportu

Ocena efektywności różnych środków transportu opiera się na prostym równaniu: t = s / v. Tutaj t oznacza czas, s to przejechana odległość, a v to prędkość. Analizując, jak długo zajmuje poszczególnym pojazdom pokonanie tej samej trasy, możemy wskazać najefektywniejszy środek transportu.

Takie badanie ułatwia wybór optymalnych rozwiązań w zakresie transportu i poprawia logistykę przewozów. Dzięki niemu udaje się zaoszczędzić zarówno czas, jak i zasoby. Dodatkowo, biorąc pod uwagę różnorodne prędkości oraz warunki panujące na drogach, to równanie staje się narzędziem do:

planowania tras,
skutecznego zarządzania czasem transportu,
optymalizacji procesów logistycznych.

Optymalizacja zużycia energii w transporcie

Optymalizacja zużycia energii w transporcie opiera się na precyzyjnej analizie czasu. Dzięki temu możemy efektywnie planować prędkość i trasy. Wiedza na temat czasu przejazdu pozwala nam wybierać takie prędkości, które maksymalnie ograniczają zużycie paliwa czy energii elektrycznej.

Kontrolując prędkość oraz starannie planując trasę, posługując się równaniem t = s / v, możemy zredukować niepotrzebne przyspieszenia i hamowania. Tego rodzaju zmiany przyczyniają się do mniejszego spalania. Kiedy trasy są optymalizowane na podstawie tych wyliczeń, poprawia się efektywność energetyczna transportu. To z kolei prowadzi do:

mniejszej emisji CO2,
obniżenia kosztów paliwa.
wprowadzenia ograniczenia strat energii,
poprawy rentowności przewozów.
zwiększonej efektywności transportu.

W rezultacie, dzięki zwiększonej efektywności, transport staje się bardziej ekologiczny i ekonomiczny.

Jak wykorzystywać wzór na czas w nauczaniu fizyki?

Wzór na czas odgrywa kluczową rolę w nauczaniu fizyki, zwłaszcza w dziedzinie kinematyki. Umożliwia uczniom dostrzeganie związku między czasem, drogą a prędkością, co w konsekwencji rozwija ich zdolności w analizie ruchu.

W kontekście edukacji fizycznej ten wzór znacząco ułatwia rozwiązywanie problemów kinematycznych, dzięki czemu matematyczne relacje stają się jasne i zrozumiałe. Uczniowie, pracując z tymi pojęciami, doskonalą:

logiczne myślenie,
precyzję w umiejętnościach matematycznych,
zdolność do głębszego zrozumienia fizyki.

Zajęcia praktyczne, które obejmują zastosowanie wzoru, sprzyjają łatwiejszemu przyswajaniu podstawowych koncepcji ruchu. Na przykład, uczniowie uczą się skutecznie:

analizować różne rodzaje ruchu,
rozpoznawać ich charakterystyki.

Stosowanie wzoru na czas w nauczaniu fizyki poszerza ich horyzonty, łącząc teorię z praktycznym podejściem. Dzięki temu uczniowie zdobywają umiejętność samodzielnego obliczania czasów trwania różnych ruchów, co stanowi fundament dla dalszej analizy dynamiki oraz wielu innych zagadnień w fizyce.

Znaczenie w edukacji i rozwiązywaniu zadań z kinematyki

Wzór na czas, czyli t = s / v, odgrywa kluczową rolę w fizyce, szczególnie w kontekście zadań kinematycznych. Umożliwia on skuteczną analizę ruchu jednostajnego, co z kolei stanowi fundament dla zrozumienia bardziej skomplikowanych zagadnień związanych z dynamiką. Dzięki temu równaniu uczniowie mogą łatwo obliczać czas, mając na uwadze dane o odległości i prędkości.

Często korzysta się z tego wzoru w kontekście takich problemów jak:

doganianie,
oddalanie,
spotkania obiektów.

To narzędzie sprzyja rozwijaniu analitycznego myślenia oraz umiejętności logicznego rozwiązywania problemów. Wykorzystanie wzoru na czas nie tylko wzbogaca ogólną wiedzę o fundamentalnych zasadach fizyki, ale także stanowi solidną bazę do dalszej eksploracji kinematyki i mechaniki.

Kalkulatory online ułatwiające obliczanie czasu

Kalkulatory online do obliczania czasu są niezwykle przydatne. Pozwalają na szybkie i precyzyjne obliczenia, bazując na wprowadzonych danych dotyczących drogi i prędkości. Użytkownicy mogą bez trudu określić czas podróży, wystarczy tylko wpisać odpowiednie wartości w kalkulator, co znacznie minimalizuje ryzyko pomyłek.

Takie narzędzia znajdują swoje miejsce zarówno w edukacji, na przykład w trakcie lekcji fizyki, jak i w codziennym planowaniu podróży oraz zarządzaniu czasem. Kiedy ktoś wpisuje w wyszukiwarkę „kalkulator czasu podróży”, często otrzymuje szereg aplikacji, które pomagają w zoptymalizowaniu działań. Umożliwiają one dokładne określenie, jak długo potrwa dany przejazd.

Dodatkowo, kalkulatory te pozwalają na konwersje w różnych jednostkach miar, co zwiększa ich wszechstronność. Dzięki nim planowanie staje się nie tylko łatwiejsze, ale także skuteczniejsze.

Jak uwzględniać różnice czasowe i strefy czasowe w obliczeniach?

Uwzględnianie różnic czasowych i stref czasowych odgrywa istotną rolę w przeprowadzaniu obliczeń. Wymaga to zastosowania standardowych jednostek czasu, takich jak sekundy, minuty i godziny. Kluczowe jest również zrozumienie bieżących przesunięć pomiędzy poszczególnymi strefami czasowymi.

Czas strefowy opiera się na lokalnym czasie określonej strefy geograficznej. Z kolei Uniwersalny Czas Koordynowany (UTC) stanowi globalny punkt odniesienia do synchronizacji czasowych. Aby właściwie obliczyć czas pomiędzy wydarzeniami, które odbywają się w różnych strefach, najpierw trzeba:

skonwertować lokalny czas na UTC,
przystąpić do wykonywania obliczeń,
przeliczyć uzyskany wynik na czas odpowiedniej strefy.

Takie podejście znacząco minimalizuje ryzyko pomyłek. Co więcej, zapewnia ono dokładne planowanie, co jest szczególnie ważne podczas organizacji międzynarodowych podróży czy w zarządzaniu czasem w systemach informatycznych.

Jednostki czasu: sekundy, minuty, godziny

Podstawowe jednostki pomiaru czasu to sekundy, minuty i godziny. W dziedzinach takich jak fizyka czy w obliczeniach związanych z kinematyką, na pierwszy plan wysuwają się sekundy, ponieważ umożliwiają one osiągnięcie wysokiej precyzji. Z drugiej strony, w życiu codziennym częściej korzystamy z minut i godzin, na przykład podczas planowania podróży czy realizacji zwykłych zadań.

Umiejętność poprawnego posługiwania się tymi jednostkami jest niezwykle istotna dla dokładnych obliczeń oraz lepszego zrozumienia wyników. O szczególnym znaczeniu mówimy, gdy musimy uwzględnić różnice lub strefy czasowe. Zrozumienie oraz umiejętność przeliczania pomiędzy sekundami, minutami i godzinami znacznie ułatwia korzystanie ze wzorów dotyczących czasu oraz analizowanie ruchu.

Czas strefowy i utc w planowaniu podróży

Czas strefowy oraz UTC to kluczowe aspekty, które warto uwzględnić przy planowaniu podróży, szczególnie tych międzynarodowych. Czas strefowy określa lokalny czas w danym regionie, który może znacząco różnić się od uniwersalnego czasu koordynowanego, znanego jako UTC. To właśnie UTC służy jako globalny standard, umożliwiający synchronizację zegarów na całym świecie.

Różnice czasowe między poszczególnymi strefami są istotne, ponieważ precyzyjnie wpływają na obliczenia dotyczące odlotów i przylotów. Na przykład:

jeżeli lot wyrusza o 15:00 UTC,
i trwa trzy godziny,
ląduje o 18:00 UTC.

Jednak już w innym kraju ta sama godzina może wyglądać zupełnie inaczej. Ignorowanie tych różnic może łatwo prowadzić do pomyłek w organizacji podróży.

Z tego powodu zrozumienie zasad dotyczących czasu strefowego oraz UTC mocno ułatwia planowanie wyjazdów. Dzięki temu można uniknąć nieporozumień związanych z czasem, co znacznie zwiększa efektywność całego procesu planowania.