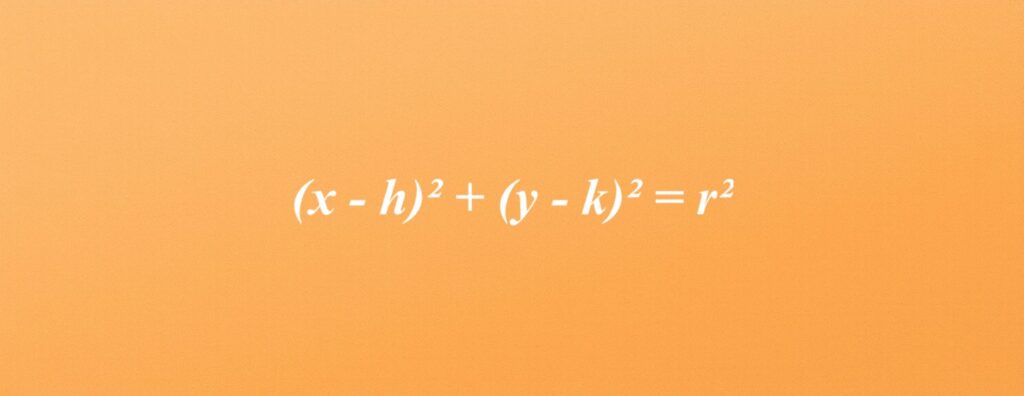Równania okręgu

Równania okręgu definiują zestaw punktów na kartezjańskiej płaszczyźnie, które znajdują się w równej odległości od stałego punktu, nazywanego środkiem okręgu. W obrębie geometrii analitycznej pełnią one niezwykle ważną rolę, stanowiąc istotne narzędzie do analizy okręgów w układzie współrzędnych. Dzięki nim możemy precyzyjnie określić położenie i kształt okręgu, co ma kluczowe znaczenie w rozwiązywaniu wielu problemów matematycznych oraz geometrycznych.

Równania okręgu przyjmują dwie główne formy:

kanoniczną,
ogólną.

Każda z nich otwiera różne możliwości interpretacji i podejścia do zagadnień związanych z okręgami. Poprzez te równania jesteśmy w stanie zidentyfikować kluczowe cechy, takie jak środek oraz promień okręgu. Co więcej, umożliwiają one także analizę powiązań między okręgami a innymi elementami znajdującymi się na płaszczyźnie.

Jak wygląda równanie okręgu w postaci kanonicznej?

Równanie okręgu w postaci kanonicznej można przedstawić jako (x – a)² + (y – b)² = r². W tym wzorze punkt S = (a, b) wskazuje na środek okręgu, natomiast r oznacza promień.

Ta forma równania jasno wytycza zarówno lokalizację środka, jak i długość promienia, co sprawia, że łatwiej jest zgłębiać i rozwiązywać problemy związane z geometrią okręgów. Wzór ten jest niezwykle przydatny, ponieważ pozwala szybko ustalić, czy dany punkt należy do okręgu, a także ułatwia obliczanie odległości od środka.

W związku z tym postać kanoniczna pełni istotną rolę w opisie okręgów w ramach geometrii analitycznej.

Jak wyznaczyć środek i promień z postaci kanonicznej?

Środek okręgu w kanonicznej formie równania to punkt S=(a, b), gdzie a i b reprezentują jego współrzędne na płaszczyźnie kartezjańskiej. Promień r można obliczyć jako pierwiastek z wartości znajdującej się po stronie równania.

Za pomocą równania (x – a)² + (y – b)² = r² bez trudu można odczytać te kluczowe informacje. Warto pamiętać, że:

poznanie środka okręgu,
obliczenie promienia,
odczytanie równania,
wyznaczenie położenia okręgu w przestrzeni,
uzyskanie pełnego obrazu.

Jak wpisać punkty płaszczyzny do równania okręgu?

Punkty umiejscowione na płaszczyźnie z odpowiadającymi im współrzędnymi (x, y) można zanalizować przy użyciu równania okręgu w formie kanonicznej: (x – a)² + (y – b)² = r². Aby dowiedzieć się, czy dany punkt leży na okręgu, wystarczy podstawić do równania swoje wartości za x i y. Środek okręgu wskazują współrzędne (a, b), a r oznacza promień.

Kiedy podstawimy konkretne wartości, możemy ustalić, czy równanie jest spełnione. Jeśli wynik to:

(x – a)² + (y – b)² = r², wtedy punkt znajduje się na obwodzie okręgu,
(x – a)² + (y – b)² ≤ r², oznacza to, że punkt leży wewnątrz okręgu,
co obejmuje przestrzeń, łącznie z brzegiem.

Taki sposób podstawiania współrzędnych znacznie ułatwia określenie, czy dany punkt należy do samego okręgu, czy znajduje się w jego wnętrzu.

Jak wygląda równanie okręgu w postaci ogólnej?

Równanie okręgu w ogólnej formie przyjmuje postać x² + y² – 2ax – 2by + c = 0, gdzie a, b i c są liczbami, które pełnią rolę współczynników. Warto zauważyć, że składniki związane z x i y są zestawione ze stałymi, co stanowi rozwinięcie postaci kanonicznej.

Aby zlokalizować środek okręgu, wystarczy skorzystać z współrzędnych (a, b). Z kolei promień można obliczyć ze wzoru r = √(a² + b² – c). Istotne jest, by wartość a² + b² – c była dodatnia, co zapewnia sensowność obliczeń.

Ta forma równania umożliwia nam analizowanie okręgu, nawet gdy nie mamy bezpośrednio danych o jego środku czy promieniu. Należy jednak przeprowadzić pewne przekształcenia, aby uzyskać te informacje.

Jak przekształcić równanie z postaci ogólnej do kanonicznej?

Aby przekształcić równanie okręgu z ogólnej formy do bardziej użytecznej wersji, stosujemy metodę uzupełniania do pełnego kwadratu. Na początku zbieramy razem składniki związane z x i y:

x² + 2gx,
y² + 2fy.

Następnie dodajemy i odejmujemy odpowiednie wartości, co pozwala nam zapisać te wyrażenia jako kwadraty dwumianów, korzystając z wzoru (x + a)² = x² + 2ax + a².

W efekcie, równanie przyjmuje formę (x + g)² + (y + f)² = r². Tutaj r² reprezentuje sumę stałych po drugiej stronie równania. Ta kanoniczna wersja ułatwia zidentyfikowanie środka okręgu, który znajduje się w punkcie (-g, -f), oraz wyznaczenie jego promienia r.

Ta technika przekształcania jest niezwykle przydatna w analizie oraz rozwiązywaniu problemów związanych z okręgami.

Jakie są warunki istnienia okręgu dla postaci ogólnej?

Warunkiem, by równanie w postaci \( x^2 + y^2 – 2ax – 2by + c = 0 \) opisywało okrąg, jest spełnienie nierówności:

a^2 + b^2 – c > 0,
tylko wtedy możemy być pewni, że promień okręgu:
r = \sqrt{a^2 + b^2 – c} jest liczbą rzeczywistą i dodatnią.
Gdy natomiast zachodzi nierówność:
a^2 + b^2 – c \leq 0, promień staje się pusty lub nawet niewymierny.

W takiej sytuacji równanie nie przedstawia okręgu, lecz może odnosić się do punktu lub całkowicie pustego zbioru. Dlatego zrozumienie tego warunku jest kluczowe dla stwierdzenia, czy dane równanie rzeczywiście definiuje okrąg.

Jak wyznaczać równanie okręgu na podstawie punktów?

Aby określić równanie okręgu na podstawie trzech punktów umiejscowionych na płaszczyźnie, zazwyczaj zaczynamy od sformułowania układu równań. Opiera się on na ogólnej formule równania okręgu, której postać wygląda następująco: x² + y² + Ax + By + C = 0. Wprowadzenie współrzędnych punktów do tego równania skutkuje uzyskaniem układu trzech równań z trzema niewiadomymi: A, B i C.

Rozwiązanie tego układu pozwala na wyznaczenie współczynników, które definiują nasz okrąg. Gdy obliczymy wartości A, B i C, jesteśmy w stanie ustalić jego środek, który znajduje się w punkcie o współrzędnych (-A/2, -B/2). Następnie, aby obliczyć promień, posługujemy się twierdzeniem Pitagorasa i ustalamy odległość między wyznaczonym środkiem a jednym z punktów na okręgu.

Dzięki tej metodzie zyskujemy precyzyjne informacje dotyczące zarówno położenia okręgu, jak i jego wymiarów na danej płaszczyźnie. Technika ta jest często wykorzystywana w zadaniach z geometrii analitycznej, pozwalając na efektywne rozwiązanie problemów dotyczących kształtów i ich właściwości.

Jak obliczyć promień okręgu na podstawie twierdzenia Pitagorasa?

Promień okręgu można łatwo obliczyć, mierząc odległość od jego środka do dowolnego punktu znajdującego się na obwodzie. Gdy znamy współrzędne środka w postaci (a, b) oraz współrzędne punktu (x, y) na okręgu, możemy zastosować twierdzenie Pitagorasa. Różnice między współrzędnymi tych punktów tworzą krótsze boki trójkąta prostokątnego. Dlatego długość promienia r obliczamy jako pierwiastek liczby będącej sumą kwadratów tych różnic:

r = √((x – a)² + (y – b)²).

Dzięki tej metodzie możemy precyzyjnie ustalić promień, wykorzystując wartości geometryczne układu współrzędnych.

Jak wyznaczyć równanie okręgu przechodzącego przez trzy punkty?

Aby znaleźć równanie okręgu przechodzącego przez trzy punkty na płaszczyźnie, możemy skorzystać z ogólnej formy: x² + y² + ax + by + c = 0. W tym równaniu wystarczy podstawić współrzędne każdego z punktów.

Po podstawieniu otrzymamy układ równań liniowych z trzema niewiadomymi: a, b oraz c. Rozwiązanie tego układu pozwala na wyznaczenie wartości tych współczynników. Mając je, możemy obliczyć środek okręgu, którego współrzędne wynikają z (-a/2, -b/2). Dodatkowo, aby znaleźć promień, możemy skorzystać ze wzoru: pierwiastek z (a²/4 + b²/4 − c).

Ta technika jest powszechnie wykorzystywana w matematyce, zwłaszcza w analizie geometrycznej oraz w zadaniach dotyczących określania parametrów okręgu na podstawie danych punktów.

Jak interpretować parametry równania okręgu?

Parametry dotyczące równania okręgu to współrzędne środka, oznaczane jako (a, b), oraz promień r. Te elementy stanowią istotne informacje na temat położenia i rozmiaru okręgu w płaszczyźnie kartezjańskiej. Środek okręgu, będący punktem wyjścia, pozwala nam mierzyć odległości do wszystkich punktów znajdujących się na jego obwodzie. Promień, z kolei, wskazuje, jak daleko te punkty oddalone są od wspomnianego środka.

Zrozumienie geometryczne tych parametrów znacząco ułatwia interpretację równania okręgu. Opisuje ono zbiór punktów, które są oddalone od środka (a, b) o stałą odległość r. Przeanalizowanie współczynników występujących w ogólnym równaniu pozwala na wyznaczenie wartości a, b oraz promienia r. Dysponując tymi informacjami, możemy łatwo określić usytuowanie okręgu oraz jego wymiary.

Te parametry odgrywają kluczową rolę zarówno w:

rysowaniu okręgów,
analizowaniu okręgów,
rozwiązywaniu problemów geometrycznych,
zrozumieniu geometrii analitycznej,
wyznaczaniu równań matematycznych.

Co oznaczają współczynniki w równaniu ogólnym i kanonicznym?

W równaniu kanonicznym okręgu, które przyjmuje formę (x – a)² + (y – b)² = r², zmienne a i b reprezentują współrzędne środka tego okręgu. Promień, oznaczany jako r, jest kluczowym elementem równania. Natomiast w jego ogólnej wersji równanie zapisuje się jako x² + y² – 2ax – 2by + c = 0. W tym kontekście a i b związane są z punktem określającym środek okręgu, czyli (a, b). Wartość c ma wpływ na wymiar promienia; można ją obliczyć przy użyciu wzoru r = √(a² + b² – c).

Dzięki analizie tych współczynników jesteśmy w stanie precyzyjnie określić zarówno lokalizację, jak i rozmiar okręgu na płaszczyźnie.

Jak odczytać położenie i wielkość okręgu z równania?

Położenie okręgu można określić, korzystając z współrzędnych jego środka, zapisanych jako (a, b). Z kolei jego rozmiar definiuje promień, oznaczany literą r. W układzie równań kanonicznych, które wyraża się wzorem (x – a)² + (y – b)² = r², zarówno środek, jak i promień są łatwo dostrzegalne. Tutaj (a, b) wskazują na punkt centralny, a r pokazuje długość promienia.

W ogólnej formie, równanie okręgu przyjmuje postać x² + y² + Dx + Ey + F = 0. Aby wydobyć współrzędne środka oraz wartość promienia, trzeba je przekształcić do formy kanonicznej, wykorzystując metodę uzupełniania kwadratów. Ciekawe jest to, że środek okręgu określa jego położenie w układzie współrzędnych, podczas gdy promień definiuje jego wielkość oraz zasięg w przestrzeni.

Te dwa kluczowe parametry – środek oraz promień – umożliwiają dokładną analizę geometryczną okręgu oraz jego relację z innymi obiektami na płaszczyźnie.

Jakie są sposoby wzajemnego położenia dwóch okręgów?

wzajemne położenie okręgów zależy od ich środków oraz promieni. Aby zrozumieć te relacje, warto porównać odległość między środkami okręgów z sumą ich promieni i różnicą promieni. Możemy wyróżnić kilka różnych układów:

Okręgi styczne zewnętrznie – w tym przypadku odległość między środkami jest równa sumie ich promieni,
Okręgi styczne wewnętrznie – tutaj odległość odpowiada różnicy promieni,
Okręgi rozłączne zewnętrznie – odległość jest wtedy większa niż suma promieni,
Okręgi rozłączne wewnętrznie – gdy mówimy o tej relacji, odległość jest mniejsza od różnicy promieni,
Okręgi przecinające się – w tym przypadku odległość jest większa od różnicy, ale mniejsza od sumy promieni.

dodatkowo, dwa okręgi mogą być współśrodkowe, co oznacza, że mają ten sam środek, ale różne promienie. Istnieje także możliwość całkowitego pokrycia się, gdy zarówno środek, jak i promień są identyczne. Liczba punktów wspólnych między okręgami zależy od wcześniej wymienionych relacji: w przypadku przecięcia znajdziemy dwa punkty, przy styczności – jeden punkt, natomiast przy rozłączności nie ma punktów wspólnych.

Jak wyliczyć odległość między środkami dwóch okręgów?

Odległość pomiędzy środkami dwóch okręgów, których współrzędne to (a1, b1) i (a2, b2), możemy określić, stosując wzór na długość odcinka łączącego te punkty. Formuła to: d = √((a2 – a1)² + (b2 – b1)²).

Ta miara pozwala nam lepiej zrozumieć wzajemne położenie okręgów, w tym:

czy mają ze sobą styczność,
czy są od siebie całkowicie oddalone,
czy się przecinają.

Dokładne wyliczenie odległości między środkami okręgów jest niezwykle istotne dla analizy ich relacji w płaszczyźnie, co może przyczynić się do lepszego zrozumienia ich wzajemnych interakcji.

Ile punktów wspólnych mogą mieć dwa okręgi?

Dwa okręgi mogą się ze sobą spotkać na wiele sposobów, co skutkuje różną liczbą punktów, w których się krzyżują.

Rozpocznijmy od przypadku, gdy okręgi są rozłączne. W tej sytuacji nie ma żadnego wspólnego punktu. Okręgi mogą być rozłączone:

wewnętrznie, co oznacza, że jeden z nich znajduje się całkowicie w obrębie drugiego,
zewnętrznie, kiedy są oddzielone.

Kiedy okręgi stykają się, mamy do czynienia z dokładnie jednym punktem wspólnym. Taki kontakt może być zarówno:

zewnętrzny,
wewnętrzny — różnice te są subtelne, ale istotne.

Gdy dwa okręgi się krzyżują, można zaobserwować dwa punkty styku.

Zupełnie inaczej wygląda sytuacja, gdy okręgi pokrywają się w całości, co prowadzi do nieskończonej liczby punktów wspólnych.

Każdy z opisanych przypadków ilustruje inne relacje, które mogą zachodzić pomiędzy okręgami.

Jak rozpoznać okręgi styczne, przecinające się i rozłączne?

Okręgi styczne spotykają się w jednym punkcie. Dzieje się to, gdy odległość między ich środkami jest równa sumie ich promieni, co określamy jako styczność zewnętrzną. Z kolei w przypadku styczności wewnętrznej, odległość odpowiada absolutnej różnicy promieni.

Gdy okręgi się przecinają, można znaleźć dwa punkty wspólne. Ta sytuacja występuje, gdy odległość pomiędzy środkami okręgów jest większa niż różnica ich promieni, ale zarazem mniejsza niż suma tych promieni. W przeciwieństwie do tego, okręgi rozłączne nie potrafią się ze sobą spotkać i nie mają punktów wspólnych.

Rozróżniamy dwa typy rozłączności:

okręgi są rozłączne zewnętrznie, gdy odległość między ich środkami przewyższa sumę promieni,
rozłączność wewnętrzna ma miejsce, gdy ta odległość jest mniejsza od różnicy promieni.

Na podstawie odległości między środkami a rozmiaru promieni możemy jednoznacznie określić, jak okręgi są położone względem siebie.

Co to jest styczna do okręgu i jak ją wyznaczyć?

Styczna do okręgu to linia, która dotyka okręgu w zaledwie jednym punkcie, znanym jako punkt styczności. W tym miejscu styczna jest prostopadła do promienia okręgu prowadzącego do tego punktu. Aby określić jej równanie, należy brać pod uwagę równanie okręgu oraz fakt, że styczna styka się z nim tylko w jednym miejscu.

W praktyce istnieje kilka metod, aby to zrobić:

znając punkt styczności oraz środek okręgu,
równanie stycznej można przedstawić jako prostą,
nachylenie stycznej to odwrotność nachylenia promienia,
wzór na styczną w punkcie (x₀, y₀) okręgu można zapisać jako: (x – a)(x₀ – a) + (y – b)(y₀ – b) = r².

Styczna do okręgu odgrywa kluczową rolę w geometrii analitycznej. Pomaga w rozwiązywaniu problemów związanych z odległościami, kątami oraz właściwościami różnych figur geometrycznych. Uwzględnienie zasady prostopadłości oraz warunku dotyczącego punktu styczności zapewnia poprawność obliczeń oraz precyzyjną identyfikację równania stycznej.

Jakie warunki musi spełniać styczność do okręgu?

Aby prosta mogła być styczna do okręgu, koniecznym warunkiem jest, aby obie figury miały właśnie jeden punkt wspólny. To oznacza, że układ równań, który opisuje zarówno prostą, jak i okrąg, musi mieć tylko jedno rozwiązanie. Co więcej, prosta styczna zawsze jest prostopadła do promienia, który łączy środek okręgu z miejscem styczności. W praktyce te zasady służą do określenia równania stycznej do danego okręgu.

Jakie są własności geometryczne okręgu w układzie współrzędnych?

Okrąg w układzie współrzędnych kartezjańskich ma kilka istotnych cech geometrycznych. Wszelkie punkty, które go tworzą, są równo oddalone od jego środka, co oznacza, że długość promienia pozostaje niezmienna. Środek okręgu pełni rolę punktu symetrii, co sprawia, że każdy punkt na obwodzie jest w równej odległości od niego. Ta właściwość zapewnia okręgowi symetrię zarówno wokół własnego środka, jak i względem osi układu współrzędnych, co znacznie ułatwia dalszą analizę geometryczną.

Cechy okręgów pozwalają na ich dokładny opis poprzez równanie w postaci kanonicznej lub ogólnej. Dzięki tym równaniom możemy precyzyjnie określić zarówno lokalizację środka, jak i długość promienia okręgu. Z znajomością tych parametrów łatwo przeliczyć obwód oraz pole powierzchni:

obwód obliczamy ze wzoru 2πr,
pole powierzchni można wyznaczyć za pomocą równania πr², gdzie r oznacza promień okręgu.

Co więcej, te właściwości stanowią fundament dla geometrii analitycznej, umożliwiając badanie relacji między różnymi okręgami oraz innymi figurami na płaszczyźnie. Podczas analizy tych relacji porównujemy środki oraz promienie okręgów, co daje cenne informacje o ich wzajemnych zależnościach.

Jak obliczyć obwód i pole okręgu na podstawie równania?

Obliczanie obwodu okręgu odbywa się według wzoru: O = 2πr, natomiast pole okręgu można uzyskać ze wzoru: P = πr², gdzie r to promień okręgu. Promień można z łatwością wyakcentować, odnosząc się do równania okręgu.

w swojej kanonicznej formie, równanie okręgu przyjmuje postać:

(x – a)² + (y – b)² = r², w której promień r jest umieszczony pod pierwiastkiem. Z kolei w ogólnej wersji, równanie można zapisać jako:

x² + y² + 2ax + 2by + c = 0. Gdy mamy już tę formę, promień można obliczyć korzystając z zależności:

r = √(a² + b² – c).

Mając obliczony promień, możemy w prosty sposób ustalić zarówno obwód, jak i pole okręgu, korzystając z wcześniej wspomnianych wzorów.

Jak rozwiązywać zadania matematyczne z równaniami okręgu?

Zadania matematyczne dotyczące równań okręgu wymagają kilku fundamentalnych umiejętności. Po pierwsze, ważne jest, aby potrafić określić równanie okręgu, bazując na takich danych, jak współrzędne środka i długość promienia, bądź punkty znajdujące się na jego obwodzie. Dodatkowo, na maturze podstawowej często spotykamy ćwiczenia, które polegają na przekształcaniu równań z postaci ogólnej do kanonicznej. Taki zabieg znacznie ułatwia odczytywanie informacji o środku oraz promieniu okręgu.

W ramach geometrii analitycznej korzystamy również z twierdzenia Pitagorasa, co umożliwia nam obliczanie długości promienia. Istotne jest także badanie wzajemnych położeń okręgów oraz identyfikowanie punktów styczności. Również zrozumienie geometrycznego znaczenia współczynników w równaniach ma ogromne znaczenie. Sprawne posługiwanie się metodami algebraicznymi w takich zadaniach to klucz do sukcesu.

Dzięki opanowaniu tych zagadnień można skutecznie podchodzić do różnych zadań maturalnych oraz ćwiczeń związanych z okręgami, co przyczynia się do lepszego zrozumienia tej tematyki.

Jakie typy zadań występują na maturze podstawowej?

Na maturze z matematyki na poziomie podstawowym zadania związane z okręgami koncentrują się na kilku kluczowych zagadnieniach. Przede wszystkim, uczniowie poznają sposób wyznaczania środka oraz obliczania promienia okręgu, korzystając z jego postaci kanonicznej i ogólnej. Dodatkowo, istotne są również zadania polegające na:

określaniu liczby punktów, w których okrąg przecina prostą,
określaniu liczby punktów, w których okrąg przecina inny okrąg,
znajdowaniu stycznych do okręgu.

To zagadnienie wymaga zrozumienia warunków styczności oraz umiejętności przekształcania równań. W praktyce uczniowie często posiłkują się analizą geometryczną, a także wykorzystują różnorodne wzory i twierdzenia matematyczne, takie jak wzór na promień czy twierdzenie Pitagorasa, aby skutecznie rozwiązać te wyzwania.

Jak stosować równania okręgu w zadaniach z geometrii analitycznej?

Równania okręgu w geometrii analitycznej odgrywają kluczową rolę w:

określaniu lokalizacji okręgu na płaszczyźnie,
badaniu interakcji z innymi figurami, takimi jak linie proste,
identyfikacji punktów, w których okrąg styka się z prostą lub z innym okręgiem.

Dodatkowo, równania te pozwalają na:

wyznaczanie linii stycznych,
obliczanie odległości pomiędzy środkami okręgów,
analizę wzajemnych relacji między okręgami, które mogą być styczne, przecinać się lub być całkowicie rozłączne.

Taka metoda daje możliwość precyzyjnego rozwiązywania różnorodnych problemów geometrycznych związanych z okręgami, co czyni ją niezwykle użyteczną w tej dziedzinie.