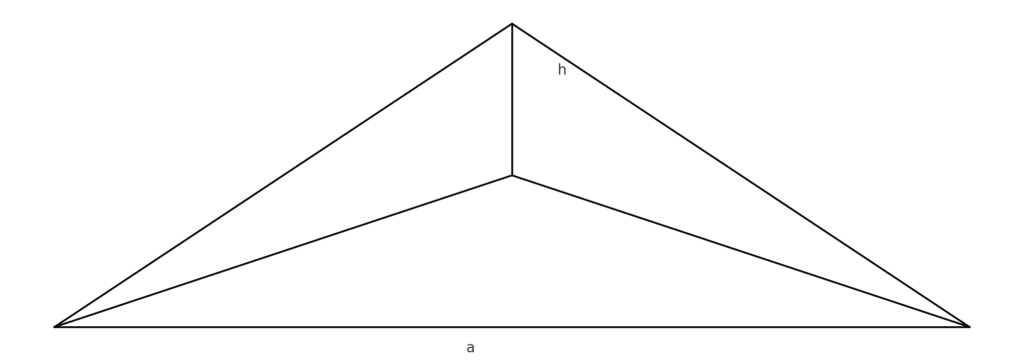
Ostrosłup prawidłowy trójkątny

Ostrosłup prawidłowy trójkątny to trójwymiarowa figura geometryczna, której podstawą jest trójkąt równoboczny. Wierzchołek tej bryły znajduje się wprost nad środkiem podstawy, w miejscu, gdzie przecinają się wysokości oraz dwusieczne trójkąta.

Cechą charakterystyczną tej bryły są:

trzy identyczne ściany boczne,
kształt równoramiennych trójkątów,
równe długości krawędzi bocznych,
równa długość wszystkich krawędzi,
ważny wielościan stanowiący podstawę dla bardziej złożonych form, takich jak czworościan foremny.

Z czego składa się ostrosłup prawidłowy trójkątny?

Ostrosłup prawidłowy trójkątny składa się z:

podstawy,
trzech ścian bocznych,
które mają kształt trójkąta równoramiennego,
każda ściana jest sobie równa.

Podstawą ostrosłupa jest trójkąt równoboczny. Wierzchołek tej figury łączy się z każdym wierzchołkiem podstawy przez krawędzie boczne. Cały ostrosłup posiada:

cztery ściany,
sześć krawędzi,
cztery wierzchołki.

Wysokość ostrosłupa to linia, która łączy wierzchołek z płaszczyzną jego podstawy. Znajduje się ona w punkcie przecięcia dwusiecznych kątów podstawy, co jest kluczowe dla obliczeń. Wysokość ściany bocznej odgrywa także ważną rolę, ponieważ wykorzystuje się ją przy wyliczaniu pola powierzchni bocznej ostrosłupa.

Ile ścian, krawędzi i wierzchołków ma ostrosłup prawidłowy trójkątny?

Ostrosłup prawidłowy trójkątny to figura składająca się z czterech ścian. Na dole znajduje się trójkąt równoboczny, który pełni rolę podstawy, a trzy pozostałe to boczne ściany w kształcie trójkątów równoramiennych. Całość ma sześć krawędzi: trzy z nich tworzą podstawę, a trzy biegną od wierzchołka ostrosłupa do wierzchołków podstawy. Warto również zauważyć, że ostrosłup dysponuje czterema wierzchołkami – trzy z nich znajdują się na dolnej części, a jeden, znajdujący się na szczycie, dopełnia całą strukturę.

Jak wygląda podstawa i ściany boczne ostrosłupa prawidłowego trójkątnego?

Podstawą ostrosłupa prawidłowego trójkątnego jest równoboczny trójkąt, który wyróżnia się trzema identycznymi bokami oraz kątami o wielkości 60°. Ściany boczne tego ostrosłupa tworzą trzy przystające trójkąty równoramienne. Ich bazą są boki trójkąta, a ramionami stają się krawędzie boczne ostrosłupa.

Krawędź boczna łączy szczyt ostrosłupa z wierzchołkiem trójkąta bazowego. Posiada ona stałą długość oraz ustalone nachylenie względem podstawy. Ponadto, wysokość każdej ze ścian bocznych to odcinek opuszczony z wierzchołka na bok podstawy trójkąta równoramiennego. Jest to istotny element, który pozwala na obliczenie powierzchni bocznej.

Jakie są najważniejsze cechy trójkąta równobocznego będącego podstawą?

Trójkąt równoboczny jest fundamentem prawidłowego ostrosłupa trójkątnego. To niesamowity kształt, który charakteryzuje się:

trzema równymi bokami,
trzema identycznymi kątami,
kątami o wartości 60°.

Interesujące jest to, że dwusieczne tych kątów spotykają się w jednym punkcie, który pełni rolę środka okręgu wpisanego oraz centrum podstawy ostrosłupa.

Promień tego okręgu wpisanego ma kluczowe znaczenie w analizach geometrycznych, a jego wartość zależy od długości boku trójkąta. Można obliczyć pole podstawy, korzystając z wzoru: P = (a²√3) / 4, gdzie a oznacza długość boku.

Te właściwości sprawiają, że trójkąt równoboczny jest niesłychanie symetryczny, co zdecydowanie ułatwia wyznaczanie parametrów ostrosłupa. W efekcie wszelkie działania związane z jego badaniem stają się znacznie prostsze i bardziej intuicyjne.

Jaki jest wzór na pole trójkąta równobocznego?

Pole trójkąta równobocznego można łatwo obliczyć, gdy znamy długość boku, oznaczonej jako a. Wystarczy zastosować wzór:

P = (a²√3) / 4.

Dzięki temu równaniu możemy szybko określić pole podstawy ostrosłupa o trójkątnej podstawie, co jest niezwykle przydatne w dalszych obliczeniach, takich jak:

pole powierzchni całkowitej,
objętość tego ostrosłupa,
rozwiązywanie różnych problemów matematycznych związanych z geometrią przestrzenną.

Co więcej, znajomość tego wzoru znacznie ułatwia rozwiązywanie różnorodnych problemów, czyniąc tę wiedzę nieocenioną w nauce.

Jaki promień ma okrąg wpisany w podstawę?

Promień okręgu wpisanego w trójkąt równoboczny można wyliczyć przy użyciu wzoru: r = (a√3) / 6, gdzie a to długość boku trójkąta. Ten promień definiuje odległość od środka trójkąta do każdej z jego krawędzi. Jest to kluczowy element w obliczeniach dotyczących geometrii ostrosłupa prawidłowego trójkątnego.

Zrozumienie tych obliczeń ma istotne znaczenie dla dalszych analiz, ponieważ:

znajomość promienia umożliwia łatwe obliczenie wysokości ostrosłupa,
praca z różnymi innymi figurami geometrycznymi staje się prostsza,
możliwość zastosowania tych wyliczeń w różnych dziedzinach nauki rośnie.

Jak obliczyć wysokość ostrosłupa prawidłowego trójkątnego?

Wysokość ostrosłupa prawidłowego trójkątnego definiuje odległość pomiędzy jego wierzchołkiem a płaszczyzną podstawy. Miejsce, w którym kończy się ta wysokość, jest usytuowane w punkcie przecięcia dwusiecznych kątów trójkąta równobocznego, który tworzy podstawę ostrosłupa. Aby znaleźć wysokość, można wykorzystać twierdzenie Pitagorasa, przyjmując długość krawędzi bocznej oraz wymiary podstawy jako kluczowe dane.

Zmierzanie wysokości ostrosłupa ma wielkie znaczenie, gdyż pozwala na obliczenie istotnych parametrów, takich jak:

objętość,
pole powierzchni,
precyzyjne określenie wymiarów.

Poprzez te zależności jesteśmy w stanie precyzyjnie określić wymiary ostrosłupa prawidłowego trójkątnego.

Czym różni się wysokość ściany bocznej od wysokości ostrosłupa?

Wysokość ostrosłupa to miara odległości, która jest mierzona prostopadle od wierzchołka do jego podstawy. Natomiast wysokość ściany bocznej odnosi się do wysokości trójkąta równoramiennego, który stanowi tę ścianę.

Ten wymiar ma istotne znaczenie podczas obliczania:

pola powierzchni bocznej ostrosłupa,
objętości ostrosłupa,
kątów nachylenia ścian bocznych,
powierzchni całkowitej ostrosłupa,
wymiarów trójkątów w podstawie.

Warto również zauważyć, że wysokość ściany bocznej jest uzależniona od kąta nachylenia krawędzi bocznej w stosunku do podstawy.

Wysokość ostrosłupa wskazuje pionową odległość od wierzchołka do jego podstawy, gdy tymczasem wysokość ściany bocznej odnosi się do trójkątnej formy ściany, która jest kluczowa podczas obliczeń związanych z powierzchnią.

Jak wykorzystać twierdzenie Pitagorasa do wyznaczania wysokości?

Twierdzenie Pitagorasa to kluczowe narzędzie, które pozwala nam obliczać wysokość ostrosłupa, korzystając z długości jego krawędzi bocznej oraz elementów podstawy. W przypadku prawidłowego ostrosłupa trójkątnego wysokość stanowi odcinek prostopadły, który prowadzi od wierzchołka do płaszczyzny podstawy. Aby określić tę wysokość, tworzymy odpowiedni trójkąt prostokątny. W nim jedna z przyprostokątnych odpowiada odległości wierzchołka od punktu, w którym wysokość podstawy się przecina, natomiast przeciwprostokątna to długość krawędzi bocznej.

Dodatkowo, aby ustalić wysokość bocznej ściany, analizujemy trójkąty prostokątne, które powstają z krawędzi bocznej i wysokości podstawy. Mając na uwadze długości krawędzi podstawy oraz krawędzi bocznej, jesteśmy w stanie łatwo obliczyć zarówno wysokość ostrosłupa, jak i wysokość jego ściany bocznej, stosując twierdzenie Pitagorasa.

Jak wyznaczyć długości krawędzi i odcinków w ostrosłupie prawidłowym trójkątnym?

Długość krawędzi podstawy ostrosłupa prawidłowego trójkątnego odpowiada bokowi trójkąta równobocznego i oznaczana jest literą a. Z kolei krawędź boczna łączy wierzchołek ostrosłupa z jednym z wierzchołków podstawy, a jej długość może być inna niż długość krawędzi podstawy.

Aby obliczyć takie elementy, jak:

wysokość ostrosłupa,
wysokość ściany bocznej,
można skorzystać z twierdzenia Pitagorasa.

W tym celu potrzebne są informacje o długościach krawędzi oraz kąt nachylenia krawędzi bocznej w odniesieniu do podstawy. Dodatkowo, pomocne są związki trygonometryczne, które umożliwiają precyzyjne obliczenia długości odcinków, uwzględniając geometryczne relacje między krawędziami a wysokościami ostrosłupa.

Jakie są podstawowe wzory dotyczące ostrosłupa prawidłowego trójkątnego?

Podstawowe wzory dotyczące ostrosłupa prawidłowego trójkątnego zawierają kilka kluczowych elementów.

Pp = (a²√3)/4, gdzie a to długość krawędzi pola podstawy,
Pb = (3ah)/2, gdzie h to wysokość ściany bocznej pola powierzchni bocznej,
Pc = (a²√3)/4 + (3ah)/2, całkowita powierzchnia ostrosłupa,
V = (a²√3/12) × H, gdzie H to wysokość całego ostrosłupa objętość,
te wzory pozwalają na precyzyjne wyznaczanie długości krawędzi, pól oraz objętości tego geometrycznego obiektu.

Jak obliczyć pole powierzchni bocznej?

Pole boczne ostrosłupa prawidłowego trójkątnego obliczamy, dodając do siebie powierzchnie trzech identycznych trójkątów równoramiennych, które stanowią ściany boczne. Wzór na obliczenie tego pola to: Pb = 3 * (1/2) * a * h. W tym równaniu „a” oznacza długość krawędzi podstawy, natomiast „h” to wysokość ściany bocznej.

Aby określić wysokość ściany bocznej h, niezbędne jest uwzględnienie kąta nachylenia krawędzi bocznej względem podstawy. Można to osiągnąć, stosując:

twierdzenie Pitagorasa,
funkcje trygonometryczne.

Dzięki takiemu podejściu wzór uwzględnia zarówno wymiary podstawy, jak i kąt nachylenia, co umożliwia precyzyjne obliczenie pola bocznego ostrosłupa.

Jak wyliczyć pole powierzchni całkowitej?

Pole całkowite ostrosłupa prawidłowego trójkątnego oblicza się poprzez dodanie pola jego podstawy do pola powierzchni bocznej. Podstawą tego ostrosłupa jest trójkąt równoboczny, którego boki mają długość a. Pole takiego trójkąta można wyznaczyć za pomocą wzoru: (a²√3)/4.

Z kolei powierzchnia boczna składa się z trzech równoramiennych trójkątów, z których każdy ma wysokość h. Ich pole można obliczyć jako (3ah)/2.

Podsumowując, całkowite pole powierzchni ostrosłupa wyraża się wzorem:

Pc = (a²√3)/4 + (3ah)/2.

Ten wzór odgrywa istotną rolę w analizie geometrycznej oraz w różnych praktycznych zastosowaniach ostrosłupa.

Jak wyznaczyć objętość ostrosłupa prawidłowego trójkątnego?

Objętość ostrosłupa prawidłowego trójkątnego można policzyć, korzystając z formuły V = (1/3) * Pp * H. Wzór ten uwzględnia:

pole podstawy, oznaczane jako Pp,
wysokość ostrosłupa, H.

W przypadku tego typu ostrosłupa jego podstawą jest trójkąt równoboczny. Pole tego trójkąta wyraża się jako Pp = (a²√3)/4, gdzie a to długość jego krawędzi.

Gdy podstawimy pole podstawy do wzoru na objętość, uzyskujemy równanie V = (a²√3 * H)/12. Warto pamiętać, że wysokość ostrosłupa, H, definiuje odległość między szczytem a płaszczyzną podstawy, co jest kluczowe dla obliczeń.

Aby dokładnie obliczyć objętość, należy starannie zmierzyć:

wysokość ostrosłupa,
długość krawędzi podstawy.

Dzięki tym pomiarom możemy precyzyjnie ustalić, jaką objętość ma ostrosłup prawidłowy trójkątny.

Jakie związki trygonometryczne stosuje się przy ostrosłupie prawidłowym trójkątnym?

W ostrosłupie prawidłowym trójkątnym istotne są podstawowe funkcje trygonometryczne: tangens, sinus oraz cosinus kąta, który opisuje nachylenie krawędzi bocznej w stosunku do podstawy.

Tangens odgrywa ważną rolę przy obliczaniu długości pewnych odcinków, takich jak wysokość ściany bocznej, odwołując się do całkowitej wysokości ostrosłupa. Równocześnie, cosinus kąta nachylenia pozwala na określenie nie tylko wysokości ściany bocznej, ale także na obliczenie powierzchni bocznej. Z kolei sinus kąta przydaje się w wyznaczaniu odległości oraz identyfikacji różnych elementów geometrycznych.

Wszystkie te funkcje trygonometryczne są niezbędne do dokładnych obliczeń wymiarów i kątów w ostrosłupie prawidłowym trójkątnym, co czyni je kluczowymi narzędziami w geometrii.

Jak tangens, sinus i cosinus kąta nachylenia krawędzi bocznej wpływają na obliczenia?

Tangens kąta nachylenia krawędzi bocznej względem podstawy jest niezwykle istotny w procesie wyznaczania wysokości ostrosłupa oraz wysokości jego bocznej ściany. Te dane pozwalają na dalsze obliczenia związane z polem powierzchni i objętością tego obiektu. Z kolei sinus kąta umożliwia określenie długości odcinka, który pełni rolę wysokości w trójkącie prostokątnym, powstałym w wyniku przekroju ostrosłupa.

Natomiast cosinus kąta pomaga ustalić długość podstawy wspomnianego trójkąta. To z kolei upraszcza oraz precyzuje nasze obliczenia dotyczące długości krawędzi bocznych. Dzięki zastosowaniu tych funkcji trygonometrycznych możemy dokładnie określić wszystkie istotne parametry geometryczne. W efekcie, uzyskujemy możliwość skutecznego obliczania pola powierzchni oraz innych istotnych wielkości ostrosłupa prawidłowego trójkątnego.

Co oznacza kąt nachylenia krawędzi bocznej do podstawy?

Kąt nachylenia krawędzi bocznej względem podstawy pozwala zobaczyć, pod jakim kątem ta krawędź wznosi się nad płaszczyzną. W przypadku ostrosłupa prawidłowego trójkątnego, ten kąt wskazuje, jak stromo krawędź boczna wznosi się nad podstawą. Znajomość tego kąta jest kluczowa, ponieważ umożliwia obliczenie długości wysokości bocznej oraz powierzchni ścian bocznych. Możemy do tego wykorzystać różnorodne funkcje trygonometryczne, takie jak:

sinus,
cosinus,
tangens,
znane twierdzenie Pitagorasa.

Właściwe zrozumienie kąta nachylenia krawędzi bocznej do podstawy jest zatem niezbędne dla precyzyjnej analizy geometrycznej ostrosłupa.

Czym jest czworościan foremny i jak się ma do ostrosłupa prawidłowego trójkątnego?

Czworościan foremny to wyjątkowy typ ostrosłupa, który charakteryzuje się tym, że każda z jego czterech ścian ma kształt trójkąta równobocznego, a wszystkie boki mają tę samą długość. W odróżnieniu od innych ostrosłupów, gdzie boczne ściany mogą przybierać różne formy oraz rozmiary, czworościan foremny wyróżnia się jednorodnością – wszystkie jego ściany są identyczne. Taka cecha nadaje mu niezwykłą symetrię, co klasyfikuje go jako wielościan foremny.

Warto zauważyć, że długość krawędzi bocznej czworościanu jest równa długości krawędzi jego podstawy. Taki układ wpływa na równomierny rozkład powierzchni oraz objętości. Aby obliczyć pole powierzchni czworościanu foremnego, wystarczy pomnożyć pole jednego trójkąta równobocznego przez cztery. Dzięki temu łatwiej jest porównywać ten wielościan z innymi ostrosłupami prawidłowymi o podobnej strukturze.

W dziedzinie geometrii przestrzennej, czworościan foremny stanowi doskonały przykład maksymalnej symetrii. Często wykorzystywany jest jako model do zrozumienia właściwości różnorodnych wielościanów.

Jak wygląda siatka ostrosłupa prawidłowego trójkątnego?

Siatka ostrosłupa prawidłowego trójkątnego składa się z jednej podstawy oraz trzech ścian bocznych. Podstawa to trójkąt równoboczny, natomiast ściany boczne to trzy przystające trójkąty równoramienne. W rozwiniętej formie tej figury geometrycznej można zauważyć:

cztery ściany,
sześć krawędzi,
cztery wierzchołki.

Taki schemat znacząco ułatwia zrozumienie struktury ostrosłupa. Dzięki niemu łatwiej jest również rysować i modelować tę bryłę. Siatka ostrosłupa prawidłowego trójkątnego ukazuje precyzyjny układ jego elementów, co jest niezwykle pomocne w nauce geometrii przestrzennej.

Jak narysować i przedstawić dynamiczną wizualizację ostrosłupa prawidłowego trójkątnego?

Rysowanie ostrosłupa prawidłowego trójkątnego rozpoczynamy od narysowania trójkąta równobocznego, który posłuży jako jego podstawa. Następnie należy dodać wierzchołek ostrosłupa, umieszczając go nad płaszczyzną tej podstawy. Z tego punktu rysujemy linie łączące go z każdym z trzech wierzchołków trójkąta.

Cały proces można przedstawić w bardziej żywym i dynamicznym stylu. Dzięki możliwości obracania bryły wokół osi oraz ukazywania siatki i przekrojów uzyskujemy wgląd w wewnętrzną strukturę ostrosłupa oraz międzykrawędziowe powiązania. Interaktywne modele zdecydowanie ułatwiają zrozumienie i zgłębianie właściwości geometrycznych ostrosłupa.

W praktyce warto korzystać z programów graficznych lub narzędzi do modelowania 3D. Te zaawansowane rozwiązania nie tylko umożliwiają tworzenie rysunków ostrosłupów z atrakcyjną wizualizacją, ale także pozwalają na dokładną analizę ich przekrojów.

Gdzie występuje ostrosłup prawidłowy trójkątny w geometrii i życiu codziennym?

Ostrosłup prawidłowy trójkątny jest fascynującym przykładem bryły w geometrii. Posiada symetryczne cechy, co sprawia, że jest idealnym modelem do nauki o wielościanach. Dzięki niemu możemy obliczać pola powierzchni i objętości, a także badać związki trygonometryczne.

W naszym codziennym życiu łatwo dostrzec ostrosłupy w architekturze, gdzie często pojawiają się w formie:

dachów,
ozdobnych elementów budynków,
harmonijnych proporcji nadających atrakcyjny wygląd przestrzeni.
kształtów powszechnie wykorzystywanych w designie,
modelarstwie, tworząc stabilne i dokładne formy.

Symetria oraz regularna struktura ostrosłupa trójkątnego stanowią solidny fundament dla zrozumienia bardziej skomplikowanych brył. Na przykład, znając ten podstawowy kształt, łatwiej jest projektować czworościany foremne.

Jakie zadania i przykłady obliczeń dotyczą ostrosłupa prawidłowego trójkątnego?

Zadania dotyczące ostrosłupa prawidłowego trójkątnego często koncentrują się na obliczaniu pól i objętości tej bryły. W takich obliczeniach z reguły korzystamy z twierdzenia Pitagorasa, aby ustalić wysokość ostrosłupa oraz długości krawędzi ścian bocznych. Na przykład, aby określić pole powierzchni bocznej, należy zsumować pola trzech trójkątnych ścian bocznych. Wysokości tych trójkątów można wyznaczyć, posługując się zależnościami trygonometrycznymi i twierdzeniem Pitagorasa.

Przyjdźmy teraz do konkretnego zadania: mając długość krawędzi podstawy a oraz wysokość ostrosłupa H, możemy obliczyć wysokość ściany bocznej. W tym celu tworzymy trójkąt prostokątny, którego boki tworzą wysokość ostrosłupa, promień okręgu wpisanego w podstawę oraz krawędź boczna. Wzór na pole powierzchni bocznej to 3 × (1/2 × a × wysokość ściany bocznej). Pole powierzchni całkowitej z kolei uzyskujemy dodając pole podstawy do pola powierzchni bocznej.

Objętość ostrosłupa możemy wyliczyć za pomocą wzoru V = (1/3) × P_p × H, gdzie P_p oznacza pole podstawy, a H to wysokość ostrosłupa. Ponieważ w naszym przypadku podstawą jest trójkąt równoboczny, pole to obliczamy z równania P_p = (a²√3)/4.

Inne zadania mogą dotyczyć określania kątów nachylenia krawędzi bocznych względem podstawy, wykorzystując funkcje trygonometryczne takie jak sinus, cosinus oraz tangens. Te obliczenia pozwalają precyzyjnie ustalić długości i kąty.

Przykładowe wyzwanie związane z rysowaniem siatki ostrosłupa polega na rozłożeniu bryły na jej podstawę oraz trzy trójkąty równoramienne. Taki sposób przedstawienia znacząco ułatwia wizualizację i prowadzenie dalszych obliczeń. Dynamiczne wizualizacje pomagają nam lepiej zrozumieć konstrukcję oraz relacje między poszczególnymi elementami ostrosłupa.

W praktyce, tego rodzaju zadania odgrywają kluczową rolę w obszarze geometrii przestrzennej, modelarstwa oraz architektury, gdzie precyzyjne obliczenia kształtów ostrosłupów są niezwykle istotne.