Ostrosłup prawidłowy sześciokątny

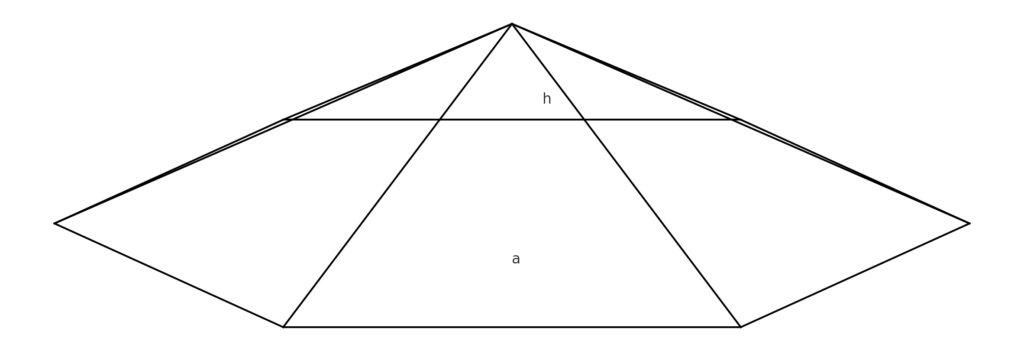
Czym jest ostrosłup prawidłowy sześciokątny?

Ostrosłup prawidłowy sześciokątny to bryła, której podstawą jest sześciokąt foremny. Wierzchołek tego ostrosłupa umiejscowiony jest dokładnie nad punktem, w którym przecięły się dłuższe przekątne sześciokąta. Struktura ta złożona jest z siedmiu ścian: jedna podstawowa oraz sześć identycznych trójkątów równoramiennych pełniących rolę ścian bocznych.

Co więcej, mamy do czynienia z ostrosłupem prostym, co oznacza, że jego wysokość jest prostopadła do powierzchni podstawy. Taka forma zapewnia mu wyraźną symetrię oraz specyficzne cechy geometryczne. Dzięki tym właściwościom ostrosłup prawidłowy sześciokątny odgrywa istotną rolę w dziedzinie stereometrii oraz precyzyjnego modelowania przestrzennego obiektów.

Jakie elementy składają się na ostrosłup prawidłowy sześciokątny?

Ostrosłup prawidłowy sześciokątny to fascynująca bryła, która ma sześciokąt foremny jako swoją podstawę. Jego boki tworzą natomiast sześć identycznych trójkątów równoramiennych, które pełnią rolę ścian bocznych. Cała figura składa się z łącznie siedmiu ścian: jednej podstawowej oraz sześciu bocznych.

Pod względem krawędzi, ostrosłup ten dysponuje 12 – z czego połowa to krawędzie podstawy, a pozostałe 6 łączą wierzchołek z wierzchołkami sześciokątnej podstawy. Jeśli chodzi o wierzchołki, jest ich 7: 6 znajduje się na podstawie, a 1 zajmuje pozycję główną, umiejscowioną tuż nad przecięciem dłuższych przekątnych.

Ta specyficzna konfiguracja krawędzi i ścian sprawia, że forma ostrosłupa jest wyjątkowo symetryczna i wyróżniająca się wśród innych brył.

Sześciokąt foremny jako podstawa

Sześciokąt foremny stanowi podstawę ostrosłupa o regularnym kształcie, który ma sześć równych boków, z długościami oznaczonymi jako „a”. Każdy z kątów wewnętrznych ma miarę 120 stopni. Ta figura geometryczna jest zbudowana z sześciu trójkątów równobocznych, co sprawia, że obliczanie pola podstawy staje się znacznie łatwiejsze – wystarczy tylko podzielić ją na mniejsze sekcje.

Przekątne sześciokąta mają kluczowe znaczenie dla analizy ostrosłupa. To one umożliwiają określenie położenia wierzchołka oraz wysokości całej bryły. W szczególności dłuższe przekątne odgrywają istotną rolę w tych obliczeniach. Sześciokąt foremny zapewnia nie tylko regularność, ale i symetrię całej konstrukcji, co dodatkowo upraszcza jej analizę.

Trójkąty równoramienne jako ściany boczne

Ściany boczne ostrosłupa prawidłowego sześciokątnego tworzą sześć identycznych trójkątów równoramiennych. Każdy z tych trójkątów ma dwa boki o równej długości, które nazywamy krawędziami bocznymi. Te krawędzie łączą wierzchołek ostrosłupa z wierzchołkami podstawy w kształcie sześciokąta.

Aby obliczyć pole powierzchni bocznej, niezbędne jest poznanie wysokości każdej ze ścian. Mierzona jest ona od szczytu trójkąta do jego podstawy. Warto również zidentyfikować kąt nachylenia ściany bocznej względem podstawy. Do tego celu przydatny jest tangens kąta nachylenia, który pozostaje stały dla wszystkich ścian bocznych, co jest efektem symetrii ostrosłupa prawidłowego.

Liczba ścian, krawędzi i wierzchołków

Ostrosłup prawidłowy sześciokątny składa się z siedmiu ścian, z czego jego podstawa przyjmuje formę foremnego sześciokąta. Pozostałe sześć ścian tworzy zestaw równoramiennych trójkątów. Cała figura ma dwanaście krawędzi: sześć z nich stanowi boki sześciokąta u podstawy, a pozostałe sześć łączy główny wierzchołek ostrosłupa z każdym z punktów na dolnej podstawie.

Wysokość ostrosłupa obejmuje siedem wierzchołków – sześć umiejscowionych w dolnej części oraz jeden na szczycie. Taka konstrukcja doskonale ilustruje twierdzenie Eulera, które dotyczy wielościanów. Mówi ono, że suma wierzchołków i ścian jest równa liczbie krawędzi powiększonej o dwa:

• V – liczba wierzchołków,
• F – liczba ścian,
• E – liczba krawędzi.

Jakie są własności geometryczne ostrosłupa prawidłowego sześciokątnego?

Ostrosłup prawidłowy sześciokątny posiada wiele interesujących właściwości geometrycznych. Jego wysokość, wznosząca się prostopadle do podstawy, przechodzi przez punkt, w którym krzyżują się dłuższe przekątne sześciokąta, będącego jego podstawą. Krawędź boczna, dłuższa od krawędzi podstawy, wpływa na ogólny kształt i proporcje tej bryły.

Ściany boczne ostrosłupa mają kształt trójkątów równoramiennych, a kąty, które tworzą z podstawą, są równe. Można je obliczyć przy użyciu funkcji trygonometrycznych, co pozwala precyzyjnie określić ich miarę. Symetria ostrosłupa ułatwia jego analizę, co czyni go bardziej przystępnym obiektem badań geometrycznych.

Na przykład, przekroje poprzeczne, które przechodzą przez wierzchołek oraz przekątne podstawy lub przez środki przeciwległych krawędzi, są pomocne w dokładniejszym badaniu struktury i właściwości ostrosłupa. Te cechy sprawiają, że ostrosłup prawidłowy sześciokątny jest istotnym zagadnieniem w geometrii przestrzennej i znajduje zastosowanie w różnych obliczeniach geometrycznych.

Wysokość ostrosłupa

Wysokość ostrosłupa prawidłowego sześciokątnego jest mierzona jako odległość prostopadła między wierzchołkiem a płaszczyzną podstawy,

ten punkt znajduje się w miejscu przecięcia dłuższych przekątnych foremnego sześciokąta.

W praktyce, wysokość ta często wynosi 6 cm lub 9 cm, co zazwyczaj odpowiada długości krawędzi podstawy.

Jest to istotny wymiar, który odgrywa kluczową rolę w obliczeniach objętości oraz w analizie innych właściwości geometrycznych tej figury.

Dodatkowo, wysokość można obliczyć, wykorzystując zależności trygonometryczne, które uwzględniają kąt, pod jakim nachylają się ściany boczne w odniesieniu do podstawy.

Wysokość ściany bocznej

Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego to segment, który rozciąga się od wierzchołka trójkąta równoramiennego aż do jego dolnej krawędzi, przy czym utrzymuje prostokątną pozycję względem podstawy. Ten trójkąt skłania się pod pewnym kątem wobec dolnej warstwy ostrosłupa.

Zrozumienie wysokości ściany bocznej jest niezbędne dla prawidłowego obliczenia pola powierzchni bocznej ostrosłupa. Co więcej, pozwala na określenie kąta nachylenia tej ściany w odniesieniu do podstawy, wykorzystując funkcję tangensa. Dzięki temu można z dużą precyzją określić zarówno rozmiar, jak i kształt ścian bocznych całej bryły.

Kąty nachylenia i ich miara

Kąt nachylenia bocznej ściany ostrosłupa sześciokątnego odnosi się do relacji między płaszczyzną tej ściany, która ma kształt trójkąta równoramiennego, a płaszczyzną podstawy, stanowiącej sześciokąt foremny. Interesujące jest to, że te kąty są identyczne dla każdej z bocznych ścian ostrosłupa. Aby je zmierzyć, można posłużyć się funkcją tangens, która definiuje się jako stosunek wysokości danego trójkąta do połowy długości boku podstawy.

Również istotny jest kąt płaski znajdujący się przy wierzchołku ostrosłupa, utworzony przez krawędzie boczne. Ten kąt ma znaczący wpływ na geometrię bryły, co z kolei przekłada się na jej wyrazistość i cechy wizualne. Analizując te kąty, możemy lepiej zrozumieć, jak boczne ściany ostrosłupa są ustawione względem podstawy, co wzbogaca naszą wiedzę o jego przestrzennej konstrukcji.

Przekątne i przekroje sześciokąta w podstawie

Przekątne sześciokąta foremnego, na którym oparty jest prawidłowy ostrosłup sześciokątny, mają długość równą dwukrotności długości boku podstawy. Wszystkie te przekątne spotykają się w jednym punkcie, stanowiącym środek sześciokąta. Nad tym punktem, na szczycie ostrosłupa, znajduje się jego wierzchołek.

Przekroje ostrosłupa są tworzone przez płaszczyzny, które przechodzą przez wierzchołek oraz przez przekątne podstawy, albo przez środki przeciwległych krawędzi sześciokąta. Przykładowo, jeśli płaszczyzna przecina ostrosłup w miejscu, gdzie znajduje się jego wysokość i dwie krawędzie boczne, pole tego przekroju będzie dwa razy większe niż pole podstawy.

Badanie tych przekrojów znacząco ułatwia zrozumienie struktury ostrosłupa. Oferuje także wgląd w jego symetrię oraz właściwości geometryczne, co jest przydatne w późniejszych obliczeniach i modelowaniu bryły.

Jak obliczyć pole powierzchni ostrosłupa prawidłowego sześciokątnego?

Aby obliczyć pole powierzchni prawidłowego ostrosłupa sześciokątnego, należy połączyć pole jego podstawy oraz pole powierzchni bocznej.

Podstawą ostrosłupa jest foremny sześciokąt, którego pole można uzyskać za pomocą wzoru:

P_p = (3√3/2) * a²

W tym równaniu ’a’ reprezentuje długość krawędzi podstawy.

Pole powierzchni bocznej składa się z sześciu identycznych trójkątów równoramiennych, które można obliczyć za pomocą wzoru:

P_b = 6 * (1/2 * a * h)

gdzie h to wysokość ściany bocznej.

Całkowite pole powierzchni ostrosłupa definiuje się równaniem:

P_c = P_p + P_b

gdzie P_b to suma pól wszystkich ścian bocznych.

Dzięki tym wzorom można precyzyjnie obliczyć całkowite pole powierzchni ostrosłupa, jeśli tylko znamy długość krawędzi podstawy oraz wysokość ścian bocznych.

Pole podstawy – wzór

Pole podstawy ostrosłupa prawidłowego sześciokątnego obliczamy w taki sam sposób, jak pole sześciokąta foremnego. Możemy skorzystać z następującego wzoru: Pp = (3√3/2) × a², gdzie 'a’ oznacza długość krawędzi podstawy.

Interesujący jest sposób, w jaki sześciokąt foremny może być podzielony na sześć równobocznych trójkątów. Każdy z tych trójkątów ma pole równe (a²√3)/4.

Znajomość tego wzoru jest niezwykle przydatna, ponieważ pozwala nie tylko na wyliczenie powierzchni podstawy, ale także:

• całkowitej powierzchni ostrosłupa,
• objętości ostrosłupa.

Pole ścian bocznych

Pole ścian bocznych ostrosłupa o sześciokątnej podstawie obliczamy, dodając pola sześciu identycznych trójkątów równoramiennych. Każda z tych ścian bocznych ma:

• podstawę równą długości krawędzi podstawy sześciokąta,
• wysokość nachyloną względem tej podstawy.

Obliczenie pola pojedynczej ściany polega na:

1. pomnożeniu długości krawędzi podstawy przez wysokość,
2. podzieleniu wyniku przez dwa.

Z tego wynika, że całkowite pole powierzchni bocznej ostrosłupa można uzyskać, mnożąc długość krawędzi podstawy przez wysokość ściany bocznej, a następnie mnożąc przez trzy. To pole odgrywa istotną rolę w obliczeniach całkowitego pola powierzchni ostrosłupa prawidłowego sześciokątnego.

Pole powierzchni całkowitej – wzór

Pole całkowite ostrosłupa prawidłowego sześciokątnego można łatwo obliczyć, posługując się następującym wzorem:

W tym równaniu:

• Pc oznacza pole powierzchni całkowitej,
• Pp to pole podstawy,
• Pb to pole powierzchni bocznych.

Podstawą ostrosłupa jest regularny sześciokąt, a powierzchnię jego podstawy obliczamy według wzoru:

W tym przypadku a odnosi się do długości boku sześciokąta.

Jeśli chodzi o powierzchnię boczną, stanowi ona sumę pól sześciu trójkątów równoramiennych, które tworzą ściany boczne ostrosłupa. Pole jednej z tych ścian można obliczyć na podstawie wzoru:

Gdzie h_b to wysokość konkretnego trójkąta bocznego. Zatem, aby obliczyć całkowitą powierzchnię boczną, stosujemy:

Dodając pole podstawy do obliczonej powierzchni bocznej, uzyskujemy całkowite pole powierzchni ostrosłupa. Tego rodzaju obliczenia są niezwykle ważne zarówno w teorii, jak i w praktycznych zastosowaniach inżynieryjnych czy architektonicznych.

Jak obliczyć objętość ostrosłupa prawidłowego sześciokątnego?

Objętość ostrosłupa prawidłowego sześciokątnego można wyliczyć przy pomocy prostego wzoru: V = (1/3) × pole podstawy × wysokość. Podstawą tego ostrosłupa jest sześciokąt foremny, którego pole oblicza się, stosując równanie: P = (3√3/2) × a², gdzie „a” oznacza długość krawędzi podstawy.

• wysokość ostrosłupa odpowiada długości prostopadłej linii,
• która łączy jego wierzchołek z płaszczyzną podstawy,
• aby uzyskać precyzyjne obliczenia objętości,
• niezbędne jest jednoczesne posiadanie informacji zarówno o polu podstawy, jak i wysokości.
• dzięki tym formułom można z łatwością przeprowadzać obliczenia geometryczne dla ostrosłupa.

Znajomość tych wartości pozwala uzyskać pełniejszy obraz cech tej bryły.

Wzór na objętość ostrosłupa

Objętość ostrosłupa prawidłowego sześciokątnego można wyznaczyć za pomocą formuły: V = (1/3) * Pp * H. W tym przypadku Pp reprezentuje pole podstawy, podczas gdy H oznacza wysokość ostrosłupa.

Podstawa tego ostrosłupa ma kształt regularnego sześciokąta o boku długości a. Dzięki temu, pole podstawy można obliczyć za pomocą wzoru: Pp = (3√3/2) * a².

Obliczając objętość, możemy skorzystać z uproszczonej formuły: V = (a² * H * √3) / 2. Dzięki temu, mając tylko długość boku podstawy i wysokość bryły, możemy szybko znaleźć objętość ostrosłupa.

Jak wykorzystać pole podstawy i wysokość?

Pole podstawy oraz wysokość prawidłowego ostrosłupa sześciokątnego odgrywają fundamentalną rolę w obliczaniu jego objętości. Podstawą jest powierzchnia sześciokąta foremnego, która stanowi bazę tej figury. Wysokość ostrosłupa to z kolei miara odległości prostopadłej między wierzchołkiem a płaszczyzną jego podstawy.

Aby znaleźć objętość, wystarczy:

1. pomnożyć pole podstawy przez wysokość,
2. podzielić otrzymany wynik przez 3.

Te istotne parametry pozwalają na precyzyjne wyliczenia geometralne, które mają zastosowanie nie tylko w matematycznych zadaniach, ale także w praktycznym wykorzystaniu ostrosłupa.

Zrozumienie tych podstawowych zasad jest niezbędne do skutecznej pracy z bryłami w geometrii.

Jak wygląda siatka ostrosłupa prawidłowego sześciokątnego?

Siatka ostrosłupa prawidłowego sześciokątnego to płaski rysunek przedstawiający sześciokąt foremny umieszczony w centrum. Ten sześciokąt tworzy podstawę ostrosłupa, a każda z jego sześciu krawędzi jest połączona z trójkątem równoramiennym, który pełni rolę ściany bocznej.

Te elementy współtworzą harmonijną figurę geometryczną, która łatwo przekształca się w trójwymiarową bryłę. Dzięki siatce możemy lepiej zobrazować konstrukcję, a także uprościć proces:

• rysowania,
• modelowania,
• analizy ostrosłupa prawidłowego sześciokątnego.

Jak rysować i modelować ostrosłup prawidłowy sześciokątny?

Rysując i modelując ostrosłup prawidłowy sześciokątny, pierwszym krokiem jest narysowanie foremnego sześciokąta, który posłuży za podstawę. Następnie na każdym z jego boków umieszczamy trójkąty równoramienne, które będą tworzyć boczne ściany. Te trójkąty spotykają się w jednym wierzchołku, kształtując całą bryłę. Aby precyzyjnie określić długości krawędzi, przydają się suwaki, które umożliwiają skalowanie oraz dostosowywanie rozmiaru naszego modelu.

Modelowanie ostrosłupa, zarówno w programach graficznych, jak i na papierze, zwraca uwagę na jego obrót w przestrzeni. To podejście pozwala na uproszczoną prezentację symetrii bryły oraz dogłębną analizę jej cech geometrycznych. Obracanie modelu sprawia, że zyskujemy możliwość obserwacji fundamentu i ścian bocznych z różnych kątów.

Symetria odgrywa kluczową rolę w procesie rysowania ostrosłupa. Bryła ta ma sześciokrotną oś symetrii, która obraca się wzdłuż linii biegnącej przez środek podstawy i wierzchołka. Uwzględnienie tego elementu nie tylko upraszcza modelowanie, ale także zwiększa walory estetyczne rysunku.

Dodatkowo, korzystanie z narzędzi takich jak suwaki czy funkcje skalowania pozwala na błyskawiczne wprowadzenie zmian w wymiarach ostrosłupa, nie naruszając przy tym jego proporcji. Jest to niezwykle ważne, zarówno w kontekście nauki geometrii przestrzennej, jak i praktycznych przedsięwzięć związanych z projektowaniem.

Skalowanie i suwak do wyznaczania długości

Skalowanie pozwala na proporcjonalną zmianę rozmiarów ostrosłupa o regularnym sześciokącie, co zapewnia zachowanie jego symetrii i proporcji.

Użycie suwaka pomaga w precyzyjnym ustawianiu długości krawędzi zarówno podstawy, jak i ścian bocznych. To narzędzie pozwala na dokładne modelowanie bryły, co jest niezbędne w wielu zastosowaniach.

Dzięki tym narzędziom można nie tylko:

• tworzyć poprawne modele,
• przeprowadzać istotne obliczenia geometryczne dotyczące długości krawędzi,
• zapewniać precyzyjność i dokładność w badaniach geometrycznych.

Obrót i symetria bryły w przestrzeni

Obracając prawidłowy ostrosłup sześciokątny w przestrzeni, możemy zbadać jego symetrię w odniesieniu do osi, która przechodzi przez szczyt oraz środek sześciokątnej podstawy. Taka osiach symetrii nie tylko ułatwia nam zrozumienie rozmieszczenia ścian bocznych, krawędzi i wierzchołków, ale także pozwala lepiej uchwycić jego formę.

Dzięki temu procesowi rotacji, mamy możliwość bardziej precyzyjnego modelowania i rysowania ostrosłupa, co z kolei sprzyja lepszej wizualizacji jego właściwości geometrycznych. Zrozumienie symetrii ostrosłupa jest istotne zarówno w kontekście nauczania geometrii przestrzennej, jak i w rzeczywistych zastosowaniach inżynieryjnych.

Jakie są przykładowe zastosowania ostrosłupa prawidłowego sześciokątnego?

Ostrosłup prawidłowy sześciokątny znalazł wiele interesujących zastosowań w dziedzinie architektury i inżynierii. Na przykład, często wykorzystuje się jego kształt do projektowania dachów altan ogrodowych, które dzięki symetrii zyskują nie tylko stabilność, ale również elegancki wygląd.

W kontekście architektury sakralnej, ten typ ostrosłupa odgrywa kluczową rolę w budowie wież kościelnych. Sześciokątna podstawa nadaje tym konstrukcjom unikalny charakter oraz wzmacnia ich trwałość. Co więcej, kształt ostrosłupa jest także inspiracją dla tradycyjnych indiańskich tipi, które dzięki swojej stożkowej formie potrafią skutecznie stawić czoła różnorodnym warunkom atmosferycznym.

Ostrosłup prawidłowy sześciokątny znajduje również swoje miejsce w matematyce, gdzie służy jako podstawowy model do analizy geometrycznej i projektowania różnorodnych struktur. Jego wszechobecność podkreśla znaczenie tego kształtu zarówno w nauce, jak i w inżynierii.

Dach altany ogrodowej

Dach altany ogrodowej zazwyczaj przyjmuje formę ostrosłupa, którego podstawa ma kształt sześciokąta. Taki projekt nie tylko wyróżnia się estetyką i symetrią, ale także zapewnia solidność całej konstrukcji.

Boczne ściany dachu tworzą równoramienne trójkąty, co nadaje mu charakterystyczny, obniżony profil. Takie rozwiązanie efektywnie odprowadza wodę, chroniąc altanę przed działaniem wilgoci.

Konstrukcja dachu w formie ostrosłupa sześciokątnego sprawia, że jest on nie tylko praktyczny, ale również bardzo atrakcyjny wizualnie. Z tego powodu często wybierany jest w projektach związanych z architekturą ogrodową.

Wieża kościoła

Kościelne wieże często przybierają formę ostrosłupa o podstawie sześciokątnej. Taki kształt, z sześciokątną podstawą i symetrycznymi trójkątnymi ścianami, nie tylko zapewnia stabilność, ale także przyciąga wzrok swoim estetycznym wyglądem. Geometryczna prostota tego projektu ułatwia zarówno jego realizację, jak i nadaje wieżom klasyczny, charakterystyczny styl, który można spotkać w architekturze sakralnej.

Wykorzystanie sześciokątnego ostrosłupa w konstrukcji wież łączy:

• praktyczność,
• estetykę,
• trwałość,
• harmonię,
• kluczowy element miejskiego krajobrazu.

To wszystko jednocześnie podkreśla piękno budowli sakralnych.

Indiańskie tipi

Indyjskie tipi to klasyczne namioty o wyjątkowym kształcie sześciokątnego ostrosłupa. Ich podstawa w formie sześciokąta oraz strome, trójkątne ściany, które spotykają się w jednym wierzchołku, doskonale współpracują, zapewniając stabilność konstrukcji. Ten design jest szczególnie ważny w obliczu silnych wiatrów, kiedy to odpowiednie rozłożenie sił staje się kluczowe.

Geometryczny kształt tych namiotów to imponujący przykład zastosowania zasad geometrii w tradycyjnej architekturze. Takie rozwiązania przyczyniają się do ich:

• trwałości,
• odporności na różnorodne warunki atmosferyczne,
• estetyki.

Dzięki temu tipi nie tylko spełniają swoją funkcję, ale również przyciągają wzrok swoją estetyką.

Co ciekawe, indyjskie tipi stały się źródłem inspiracji dla projektantów w różnych dziedzinach, w tym architekturze oraz wzornictwie, pokazując, jak tradycyjne formy mogą być używane w nowoczesnych koncepcjach.

Jak analizować przekroje i własności ostrosłupa prawidłowego sześciokątnego?

Analiza przekrojów ostrosłupa prawidłowego sześciokątnego polega na identyfikacji płaszczyzn przenikających tę bryłę, co pozwala na lepsze zrozumienie jej struktury geometrycznej.

Kiedy przekrój przechodzi przez środki przeciwległych krawędzi podstawy, uzyskujemy sześciokąt. To symetryczne odwzorowanie ukazuje interesujące relacje między krawędziami bocznymi a podstawą. Z drugiej strony, przekrój, który przeciąga się przez wierzchołek ostrosłupa oraz przekątne sześciokątnej podstawy, prowadzi do utworzenia trójkątnego kształtu. Taki przekrój daje możliwość oceny:

• wysokości ścian bocznych,
• kątów ich nachylenia względem podstawy.

Warto zwrócić uwagę, że pole tego trójkątnego przekroju, zawierającego wysokość ostrosłupa i dwie krawędzie boczne, jest dwukrotnie większe od pola jego podstawy.

Przeanalizowanie tych przekrojów pozwala na dokładne określenie właściwości geometrycznych ostrosłupa. To z kolei odgrywa kluczową rolę w obliczeniach dotyczących:

• pola powierzchni,
• objętości,
• kątów nachylenia.

Te informacje mają istotne znaczenie zarówno w kontekście teoretycznym, jak i praktycznych zastosowań ostrosłupa.

Przekrój przez środki przeciwległych krawędzi

Przekrój utworzony przez środki przeciwległych krawędzi podstawy ostrosłupa prawidłowego sześciokątnego generuje płaszczyznę, która przechodzi przez jego centrum, ujawniając symetrię tej niezwykłej bryły. Ta konkretna płaszczyzna łączy środki dwóch par krawędzi, co umożliwia precyzyjną analizę wymiarów oraz układów między krawędziami a wierzchołkiem ostrosłupa.

Taki przekrój jest nieoceniony w określaniu wysokości bryły oraz kątów nachylenia ścian bocznych z perspektywy geometrii przestrzennej. Badanie tych przekrojów ma kluczowe znaczenie, na przykład, w trakcie rozwiązywania problemów geometrycznych czy podczas modelowania brył.

Ułatwia to nie tylko zrozumienie struktury ostrosłupa, ale także odkrywanie jego wewnętrznych relacji i symetrii. Dodatkowo, pozwala na zgłębianie złożoności form geometrycznych, które nas otaczają.

Przekrój przez wierzchołek ostrosłupa i przekątne podstawy

Przekrój przez wierzchołek ostrosłupa sześciokątnego, wykonany w płaszczyźnie symetrii, dzieli bryłę na dwie jednakowe części. W tym przekroju uwzględnione są:

• wierzchołek,
• dwie przekątne sześciokąta,
• będącego podstawą ostrosłupa.

Co ciekawe, pole tego przekroju jest dwukrotnie większe niż pole samej podstawy.

Dokładna analiza tego fragmentu daje możliwość ustalenia wysokości ostrosłupa oraz kątów nachylenia bocznych ścian w stosunku do podstawy. Dodatkowo, przy jego pomocy można zdefiniować zależności między krawędziami. Ten rodzaj przekroju odgrywa kluczową rolę w geometrii przestrzennej, ułatwiając zarówno rozwiązywanie problemów, jak i lepsze zrozumienie budowy ostrosłupa.

Jak rozwiązywać zadania z ostrosłupem prawidłowym sześciokątnym?

Rozwiązywanie zadań dotyczących ostrosłupa prawidłowego sześciokątnego wiąże się z koniecznością zrozumienia kilku istotnych zagadnień. Na początek warto zapoznać się z:

• długościami krawędzi podstawy,
• wysokością całej bryły,
• wzorami, które dotyczą pola powierzchni podstawy,
• wzorami dotyczącymi bocznych ścian, mających kształt trójkątów równoramiennych.

Jednym z fundamentalnych etapów jest obliczenie całkowitego pola powierzchni. Aby to zrobić, należy zsumować pole podstawy z polem wszystkich ścian bocznych. Często pojawia się także zadanie dotyczące wyznaczenia objętości ostrosłupa. W takim przypadku:

1. mnożymy pole podstawy przez wysokość,
2. dzielimy przez trzy.

Poziom trudności takich zadań może być różny. Możesz spotkać się zarówno z:

• prostymi obliczeniami długości i powierzchni,
• bardziej złożonymi zagadnieniami, dotyczącymi analizy przekrojów,
• kątów nachylenia ścian bocznych.

Umiejętność nakreślenia siatki ostrosłupa jest niezwykle cenna, ponieważ ułatwia wizualizację i modelowanie tej bryły, zwłaszcza w trudniejszych zadaniach geometrycznych.

W praktyce, aby skutecznie rozwiązywać takie zadania, potrzebna jest systematyczność w stosowaniu wzorów, przekształcaniu równań oraz przeprowadzaniu analiz geometrycznych.

Typowe przykłady i poziom trudności

Typowe zadania dotyczące ostrosłupa prawidłowego sześciokątnego obejmują różnorodne obliczenia, takie jak:

• powierzchnia,
• objętość,
• długość krawędzi,
• wysokość.

Poziom trudności tych zadań może się znacznie różnić – od prostu kalkulacji, przez bardziej zaawansowane, wymagające analizy przekrojów lub zrozumienia kątów nachylenia ścian bocznych. Takie wyzwania nie tylko rozwijają umiejętności w zakresie geometrii i stereometrii, ale także pozwalają na praktyczne wykorzystanie wzorów oraz zrozumienie właściwości ostrosłupa. Warto zatem podjąć się tych zadań, aby lepiej poznać ten ciekawy temat.

Obliczenia geometryczne dotyczące krawędzi i wysokości

Obliczenia dotyczące ostrosłupa prawidłowego sześciokątnego odgrywają kluczową rolę w jego zrozumieniu. Na początek skupiamy się na:

• długościach krawędzi podstawy,
• krawędzi bocznych,
• wysokości ostrosłupa,
• wymiarach jego ścian.

Podstawą ostrosłupa jest sześciokąt foremny, którego długość boku oznaczamy literą a. Natomiast krawędź boczna, czyli krawędź ściany bocznej, to długość ramienia trójkąta równoramiennego, którą symbolizujemy literą l.

Wysokość ostrosłupa (h) definiuje odległość między wierzchołkiem a płaszczyzną podstawy. Warto również zwrócić uwagę na wysokość ściany bocznej (hb), która odpowiada wysokości trójkąta bocznego, tworzącego tę ścianę.

Aby określić wysokość ściany bocznej oraz kąt nachylenia, korzystamy z wzorów trygonometrycznych. Na przykład, dysponując wysokością ostrosłupa i długością krawędzi podstawy, możemy obliczyć wysokość ściany bocznej, posługując się funkcjami trygonometrycznymi, takimi jak sinus i cosinus. Kąt nachylenia natomiast ustalamy, analizując zależności między krawędziami bocznymi a podstawą.

Dokładne obliczenia tych parametrów są nie tylko istotne dla wyznaczenia powierzchni całkowitej oraz objętości ostrosłupa, ale mają również praktyczne zastosowanie. Precyzyjne mierzenie krawędzi i wysokości jest kluczowe w procesach takich jak modelowanie brył czy projektowanie elementów architektonicznych.