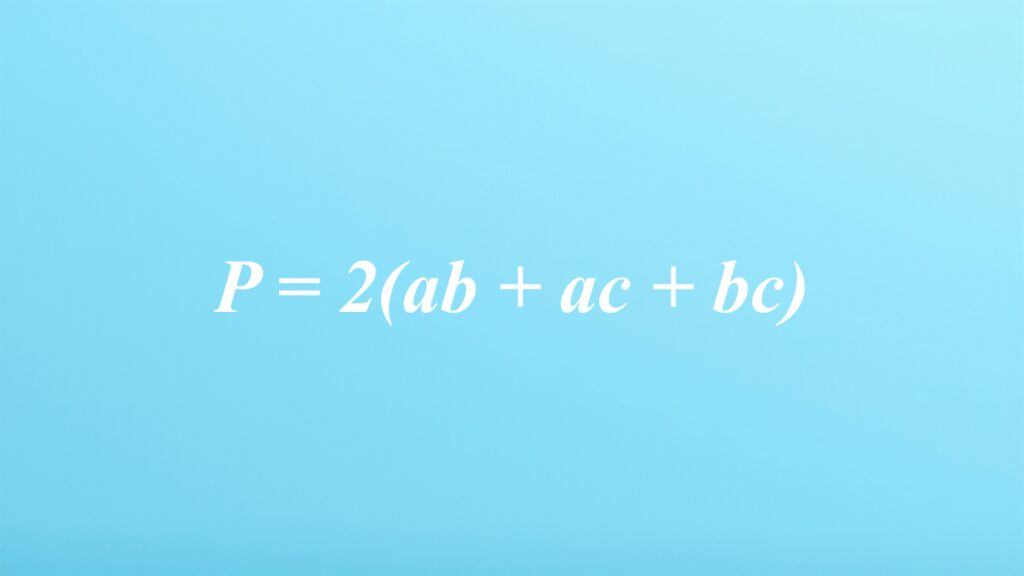Pole powierzchni prostopadłościanu
Prostopadłościan to bryła przestrzenna, złożona z sześciu ścian w kształcie prostokątów, w tym dwóch podstaw. Aby obliczyć jego pole powierzchni, korzystamy ze wzoru obejmującego wszystkie te ściany. Całkowite pole powierzchni wyrażane jest równaniem: P = 2(ab + ac + bc), gdzie a, b i c oznaczają długości krawędzi.
Wzór ten jest kluczowy dla precyzyjnego obliczenia powierzchni prostopadłościanu, ponieważ uwzględnia każdą z sześciu ścian figury. Dzięki niemu możemy łatwo określić pole dla dowolnych wymiarów tej bryły.
Stosowanie tego wzoru ma istotne znaczenie w różnych dziedzinach nauki i techniki wymagających dokładnych pomiarów. Ponadto pomaga on lepiej zrozumieć zasady geometrii przestrzennej oraz ich praktyczne zastosowania zarówno w codziennym życiu, jak i różnych sektorach przemysłu.
Wzór na pole powierzchni całkowitej prostopadłościanu
Całkowite pole powierzchni prostopadłościanu obliczamy za pomocą wzoru ( P_C = 2(ab + ac + bc) ), gdzie ( a ), ( b ) i ( c ) to długości jego krawędzi. Ta bryła ma sześć ścian, z których każda jest prostokątem.
Przeciwległe ściany są identyczne i tworzą trzy pary. Aby znaleźć całkowitą powierzchnię, należy dodać pola wszystkich trzech par ścian zgodnie z podanym wzorem. Dzięki temu precyzyjnie wyznaczamy łączną powierzchnię bryły.
Wzór na pole podstawy prostopadłościanu
Pole podstawy prostopadłościanu obliczamy używając wzoru P = a * b, gdzie a i b reprezentują długości boków tej podstawy. To pole odgrywa istotną rolę przy określaniu całkowitej powierzchni prostopadłościanu. Aby je znaleźć, wystarczy pomnożyć długości boków prostokąta tworzącego podstawę. Ta umiejętność jest niezbędna podczas dalszych obliczeń związanych z powierzchnią całej bryły.
Wzór na pole boczne prostopadłościanu
Aby wyznaczyć pole boczne prostopadłościanu, posługujemy się wzorem: P_b = 2(ac + bc). Oznacza to, że dodajemy pola wszystkich ścian bocznych, które mają kształt prostokątów. Ten wzór uwzględnia długości boków a, b i c tej bryły. Dzięki niemu szybko możemy obliczyć wartość pola bocznego prostopadłościanu. W geometrii przestrzennej pole boczne odgrywa znaczącą rolę i jest często używane przy projektowaniu oraz w architekturze.
Jak obliczamy pole powierzchni prostopadłościanu?
Aby obliczyć pole powierzchni prostopadłościanu, musimy znać długości jego krawędzi, które definiują wymiary ścian. Pole całkowite tej bryły uzyskujemy, sumując pola wszystkich par ścian oraz podstaw, a następnie mnożąc wynik przez dwa. Wzór na to pole wygląda następująco: P = 2(ab + ac + bc), gdzie a, b i c reprezentują długości boków.
Przykładowo, jeśli mamy prostopadłościan o wymiarach a = 3 cm, b = 4 cm i c = 5 cm:
- ab daje nam 12 cm²,
- ac wynosi 15 cm²,
- bc to 20 cm².
Następnie dodajemy te wartości i podwajamy sumę: P_C = 2(12 + 15 + 20) = 94 cm². Dzięki temu otrzymujemy całkowitą powierzchnię prostopadłościanu.
Taka metoda umożliwia szybkie i precyzyjne określenie pola powierzchni dowolnego prostopadłościanu po dostarczeniu odpowiednich wymiarów jego boków.
Jak obliczyć pole powierzchni prostopadłościanu znając boki?
Aby obliczyć całkowitą powierzchnię prostopadłościanu, potrzebujemy długości jego krawędzi: a, b oraz c. Formuła jest następująca: P_C = 2(ab + ac + bc).
- wyznaczamy pola dla każdej pary przeciwległych ścian — są to ab, ac i bc,
- sumujemy te wartości,
- otrzymany wynik mnożymy przez dwa, co pozwala uwzględnić wszystkie ściany bryły.
Dzięki temu precyzyjnie określamy całkowitą powierzchnię prostopadłościanu.
Jak obliczyć powierzchnię boczną prostopadłościanu, znając obwód podstawy i wysokość bryły?
Aby obliczyć powierzchnię boczną prostopadłościanu, musimy znać obwód jego podstawy oraz wysokość bryły. Obwód ten można wyrazić wzorem 2(a + b), gdzie a i b to długości boków prostokąta stanowiącego podstawę. Mając już obwód, wystarczy pomnożyć go przez wysokość prostopadłościanu (c), aby uzyskać powierzchnię boczną. Wzór na nią wygląda następująco: P_b = 2(a + b) * c. Dzięki tym kalkulacjom możemy precyzyjnie określić pole powierzchni bocznej, co ma kluczowe znaczenie w różnych projektach inżynieryjnych i architektonicznych.
Przykład: Jak znaleźć pole powierzchni prostopadłościanu?
Aby obliczyć pole powierzchni prostopadłościanu, korzystamy ze wzoru: , gdzie ( a ), ( b ) i ( h ) to długości jego krawędzi. Przyjrzyjmy się przykładowi dla prostopadłościanu o wymiarach 30 cm x 20 cm x 25 cm.
Najpierw obliczamy pole każdej pary ścian:
- ściana z bokami 30 cm i 20 cm ma powierzchnię 30 cm * 20 cm = 600 cm^2
- powierzchnia ściany o wymiarach 30 cm na 25 cm wynosi 30 cm * 25 cm = 750 cm^2,
- dla ściany mierzącej 20 cm na 25 cm otrzymujemy 20 cm * 25 cm = 500 cm^2
Następnie sumujemy te wartości:
- łączna suma wynosi: 600 + 750 + 500 = 1850 cm^2
Na koniec mnożymy tę sumę przez dwa, aby uzyskać całkowite pole powierzchni:
- całkowite pole powierzchni wyraża się jako: P = 2 * 1850 = 3700 cm^2.
Zatem pole powierzchni tego prostopadłościanu wynosi dokładnie 3700 cm^2.
Jakie jest pole powierzchni prostopadłościanu o wymiarach 4 4 10?
Aby obliczyć pole powierzchni prostopadłościanu o wymiarach 4, 4 i 10, stosujemy wzór: ( P_C = 2(ab + ac + bc) ). W naszym przypadku wartości są następujące:
- a = 4,
- b = 4,
- c = 10.
Podstawmy te liczby do wzoru:
P_C = 2 * (4 * 4 + 4 * 10 + 4 * 10)
Obliczenia prowadzą do:
P_C = 2 * (16 + 40 + 40)
Wynik końcowy to:
P_C = 2 * 96
Zatem pole powierzchni wynosi dokładnie 192 cm².